数据集(Data Set)

数据集说明

原理介绍

  Data Set:对于机器学习领域来说，数据集的选择是至关重要的，一个数据集的好坏往往可以直接决定聚类结果，通常一个算法很难适用于所有的数据集。因此我们需要设计各种数据集，并且分析哪一种数据类型适合用哪一种算法，只有这样，在今后的使用中才能得心应手。考虑到数据集的适应性，设计了以下五种不同的数据集，包括水平竖直型数据，斜线型数据，圆形数据，高斯型数据和混合型数据。

代码实战

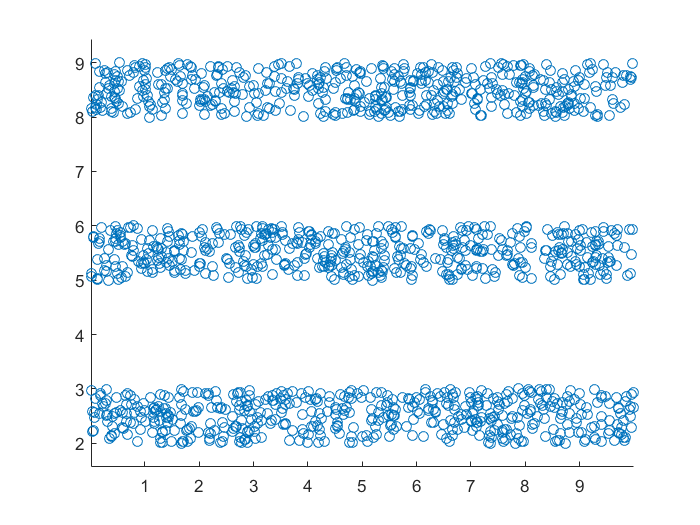
line_data.m

clear;clc;close all;
hold on;
axis equal;
%线的长度 
long=[10,10,10];
%线的宽度
wide=[1,1,1];
%线的起始位置
x_0=[0,0,0];
y_0=[2,5,8];
%每一条线上元素的个数
num=[500,500,500];
data_temp=zeros(2,sum(num));
for i=1:length(long)
    if i==1
        data_temp(:,1:num(i))=[rand(1,num(i))*long(i)+x_0(i);rand(1,num(i))*wide(i)+y_0(i)];
    else
        data_temp(:,sum(num(1:i-1))+1:sum(num(1:i)))=[rand(1,sum(num(1:i))-sum(num(1:i-1)))*long(i)+x_0(i);rand(1,sum(num(1:i))-sum(num(1:i-1)))*wide(i)+y_0(i)];
    end
end
%随机打乱顺序
randIndex = randperm(size(data_temp,2));
data=data_temp(:,randIndex);
plot(data(1,:),data(2,:),'o');
hold off;

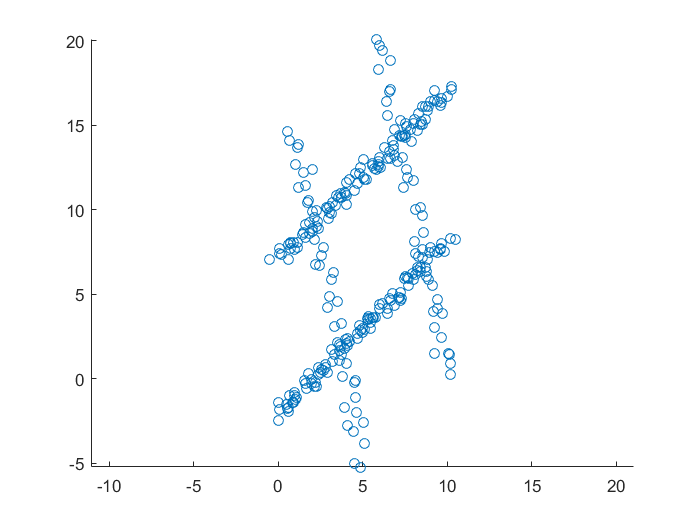
slash_data.m

clear;clc;close all;
hold on;
axis equal;
%x的起始和终止位置
begend=[0,0,1,6;...
    10,10,5,10];
%斜率和截距
kb=[1,1,-5,-5;...
    -2,7,20,50];
data_temp=[];
for i=1:size(begend,2)
    x=begend(1,i):0.1:begend(2,i);
    data_temp=[data_temp,[x+rand(1,length(x))-0.5;kb(1,i)*x+kb(2,i)+rand(1,length(x))-0.5]];
end
%随机打乱顺序
randIndex = randperm(size(data_temp,2));
data=data_temp(:,randIndex);
plot(data(1,:),data(2,:),'o');
hold off;

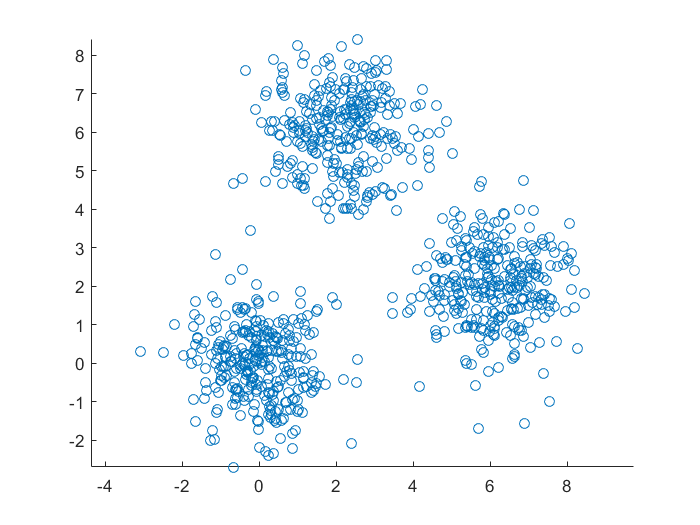
gauss_data.m

clear;clc;close all;
hold on;
axis equal;
%簇个数
num=3;
%每一类的个数
number=300;
%u和sigma
data_temp=zeros(2,num*number);
usigma_x=[0,2,6;
    1,1,1];
usigma_y=[0,6,2;
    1,1,1];
for i=1:num
    data_temp(:,(i-1)*number+1:i*number)=[normrnd(usigma_x(1,i),usigma_x(2,i),1,number);normrnd(usigma_y(1,i),usigma_y(2,i),1,number)];
end
%随机打乱顺序
randIndex = randperm(size(data_temp,2));
data=data_temp(:,randIndex);
plot(data(1,:),data(2,:),'o');
hold off;

cicle_data.m

clear;clc;close all;
hold on;
axis equal;
theta = 0:0.05:2*pi;
x=cos(theta);
y=sin(theta);
%椭圆方程(x+x0)^2/a^2+(y+y0)^2/b^2=1
ab=[3,4,6,10;...
    3,4,6,10];
xy_0=[0,0,0,0;...
    0,0,0,0];
data_temp=zeros(2,length(theta)*size(ab,2));
for i=1:size(ab,2)
    data_temp(:,(i-1)*length(theta)+1:i*length(theta))=([x;y].*repmat(ab(:,i),1,length(theta)))+repmat(xy_0(:,i),1,length(theta));
end
%随机打乱顺序
randIndex = randperm(size(data_temp,2));
data=data_temp(:,randIndex);
plot(data(1,:),data(2,:),'o');
hold off;

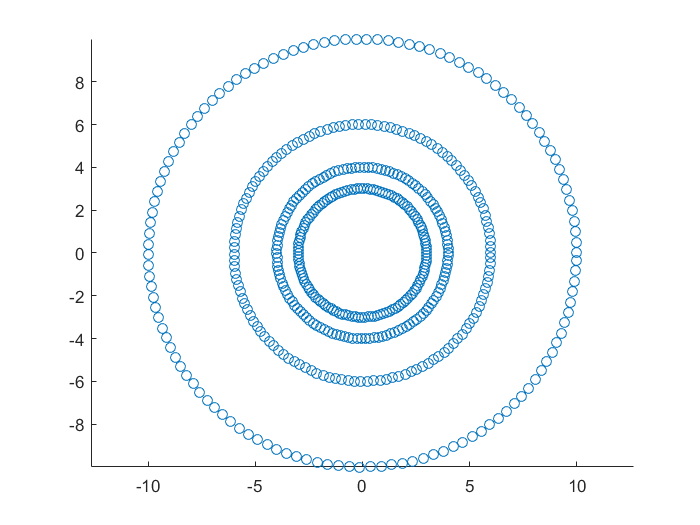
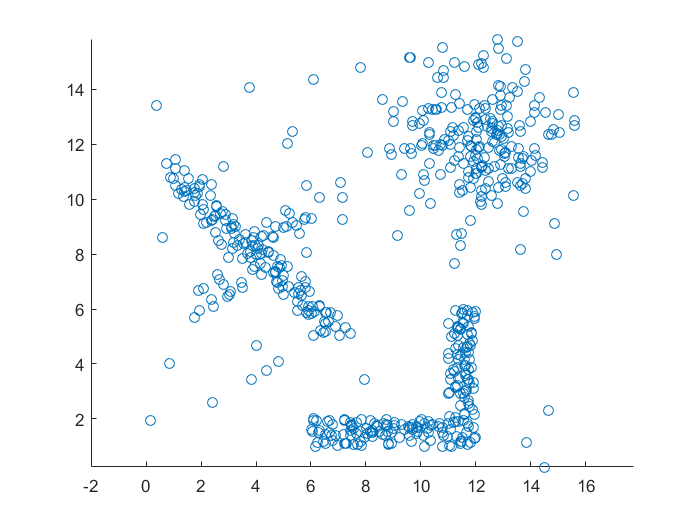
mixture_data.m

由上面的四种数据集组合之后可以形成混合数据集。

clear;clc;close all;
hold on;
axis equal;
%x1的起始和终止位置
x_1=2:0.1:6;
%x1的斜率和截距
kb_1=[1;4];
data_1=[x_1+rand(1,length(x_1))-0.5;kb_1(1)*x_1+kb_1(2)+rand(1,length(x_1))-0.5];
%x2的起始和终止位置
x_2=1:0.05:7;
%x2的斜率和截距
kb_2=[-1;12];
data_2=[x_2+rand(1,length(x_2))-0.5;kb_2(1)*x_2+kb_2(2)+rand(1,length(x_2))-0.5];
%产生高斯数据集
data_3=normrnd(12,1.5,2,200);
%线的长度 
long=[5,1];
%线的宽度
wide=[1,5];
%线的起始位置
x_0=[6,11];
y_0=[1,1];
%每一条线上元素的个数
num=[100,100];
data_4=zeros(2,sum(num));
for i=1:length(long)
    if i==1
        data_4(:,1:num(i))=[rand(1,num(i))*long(i)+x_0(i);rand(1,num(i))*wide(i)+y_0(i)];
    else
        data_4(:,sum(num(1:i-1))+1:sum(num(1:i)))=[rand(1,sum(num(1:i))-sum(num(1:i-1)))*long(i)+x_0(i);rand(1,sum(num(1:i))-sum(num(1:i-1)))*wide(i)+y_0(i)];
    end
end
%产生噪声点
data_5=rand(2,38)*16;
data_temp=[data_1,data_2,data_3,data_4,data_5];
%随机打乱顺序
randIndex = randperm(size(data_temp,2));
data=data_temp(:,randIndex);
plot(data(1,:),data(2,:),'o');
hold off;