K-Means聚类方法

原理解读

K-Means :随机选取N个对象作为初始的聚类中心，然后计算每个对象与各个种子聚类中心之间的距离，把每个对象分配给距离它最近的聚类中心。每分配一个样本，聚类中心会根据聚类中现有的对象被重新计算。这个过程将不断重复直到满足某个终止条件。

核心思想

1. 求出N个类别的聚类中心a₁,a₂, … ,a_N
$$a_i=\frac {1}{\lvert C_i \rvert}\underset{x_i \in C_j}{\sum}{x_i}$$
2. 对于每个样本x_j，将其标记为距离类别中心a_i最近的一类
$$x_j \in C_i \ , \ 其中k=\underset{i,a_i \in C_k}{arg \ min}\ d(x_j,a_i)$$
3. 重复步骤1，2直到满足某个终止条件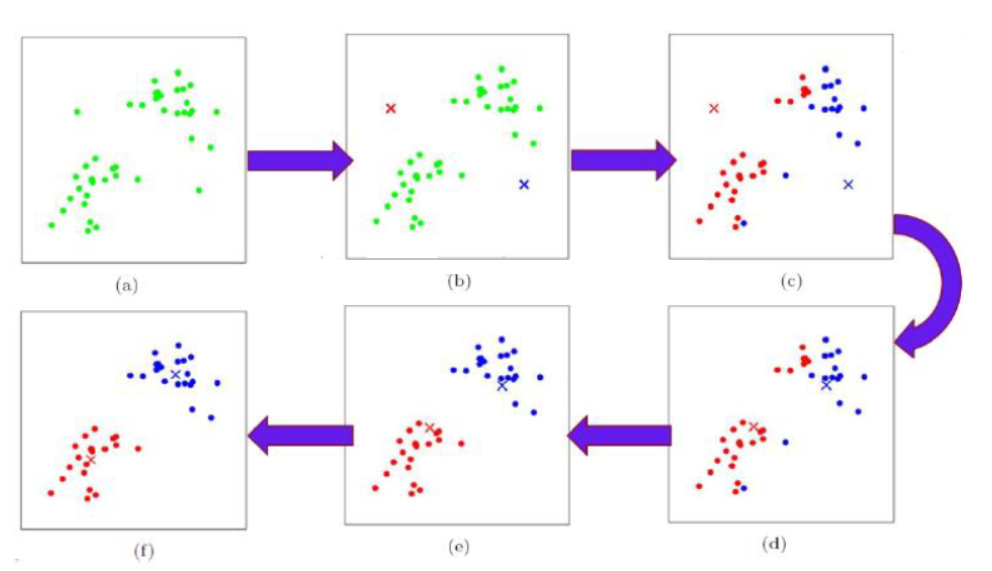
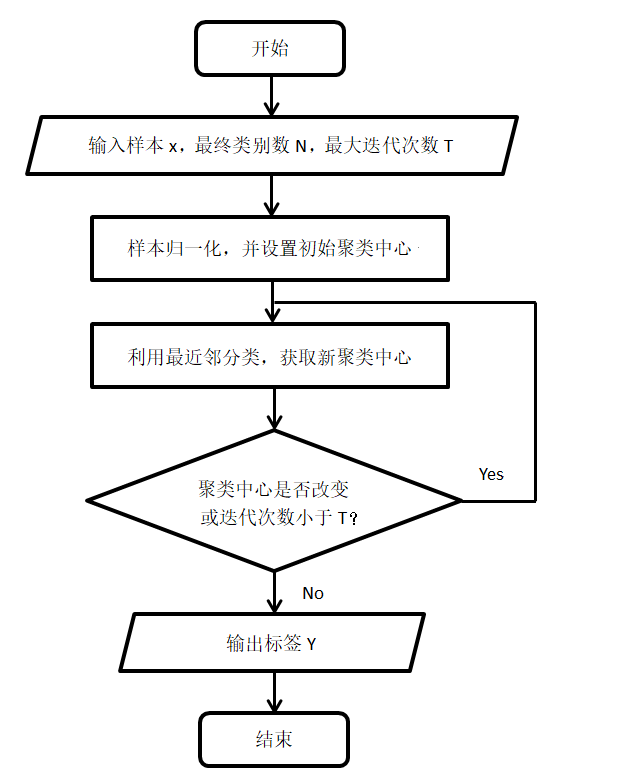
KMEANS

算法流程

KMEANS

代码实战

代码中所用数据集可以查看相关文档，数据集(Data Set)

KMEANS_main.m

clear;clc;close all;
load('..\\cluster_gauss.mat');
%输入x的矩阵
x=data;
randIndex = randperm(size(x,2));
x=x(:,randIndex);
%类别数目，请输入大于1的数
class_num=3;
%样本数
sample_num=size(x,2);
%特征数目
feat_num=size(x,1);
%尺度缩放到0-1
x_scale=zeros(size(x));
for i=1:feat_num
    x_scale(i,:)=(x(i,:)-min(x(i,:)))/(max(x(i,:))-min(x(i,:)));
end
%类别中心位置
loc_center=zeros(feat_num,class_num);
%如果类别数大于样本数或者类别数小于1，则无法分类
if class_num>sample_num||class_num<1
    disp('ERROR!')
else
    %如果类别数等于1，则所有的样本都属于该类别,聚类中心为所有样本的中点
    if class_num==1
        y=ones(1,sample_num);
        loc_center(:,1)=sum(x,2)/sample_num;
        k=0;
    else
        %取前class_num个样本作为初始类别
        loc_center=x_scale(:,1:class_num);
        %ISO聚类法
        [y,loc_center,k]=KMEANS_classify(x_scale,loc_center,sample_num,class_num);
        %将缩放后的聚类中心复原
        for i=1:feat_num
            loc_center(i,:)=loc_center(i,:)*(max(x(i,:))-min(x(i,:)))+min(x(i,:));
        end
    end
    if k>=1000
        disp('Incorrect Classify')
    else
        %如果数据的特征是二维的，可以绘图表示
        if feat_num==2
            KMEANS_display(x,y,loc_center,sample_num,class_num)
        else
            disp('The Feature Is Not Two-Dimensional');
        end
    end
end

KMEANS_classify.m

function [y,loc_center,k]=KMEANS_classify(x_scale,loc_center,sample_num,class_num)
%设置迭代次数
k=0;
while 1
    %初始化最新的分类中心
    loc_center_new=zeros(size(loc_center));
    distance=zeros(class_num,sample_num);
    %distance为每一个样本到每一类的距离
    for i=1:class_num
        distance(i,:)=sum((x_scale-repmat(loc_center(:,i),1,sample_num)).^2);
    end
    %求出每个样本到哪一类最近
    [~,y]=min(distance);
    %更新分类中心
    for i=1:class_num
        loc_center_new(:,i)=sum(x_scale(:,y==i),2)/sum(y==i);
    end
    %如果分类中心和上一次分类中心相等则分类完毕
    if isequal(loc_center_new,loc_center)
        break;
    %否则继续分类
    else
        loc_center=loc_center_new;
        k=k+1;
        %如果分类次数达到1000仍然没有结束，则强制分类结束
        if k>=1000
            break;
        end
    end
end

KMEANS_display.m

function KMEANS_display(x,y,loc_center,sample_num,class_num)
hold on;
color_bar=zeros(class_num,3);
%画出每一类的聚类中心，用*表示
for i=1:class_num
    color_bar(i,:)=[rand(1),rand(1),rand(1)];
    plot(loc_center(1,i),loc_center(2,i),'color',color_bar(i,:),'marker','*')
end
%画出每一类的样本数据，用o表示
for i=1:sample_num
    plot(x(1,i),x(2,i),'color',color_bar(y(i),:),'marker','o');
end
hold off;

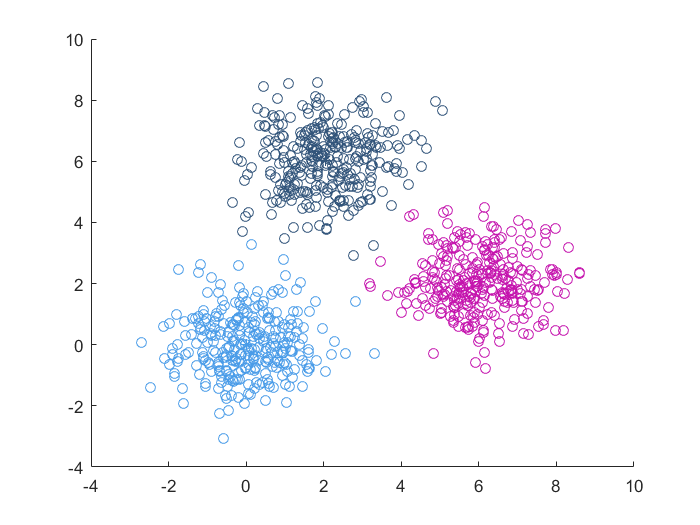
实验结果

KMEANS

性能比较

优点：
- 算法简单，容易理解
- 大数据集时，对噪声数据不敏感

缺点：

对初始中心点敏感
需要在测试前知道类别的个数
只适合分布呈凸型或者球形的数据集
对于高维数据，距离的度量并不是很好