快速搜索聚类(CFDP)

快速搜索聚类方法

原理解读

  CFDP(Clustering By Fast Search And Find Of Density Peaksd):经典的聚类算法K-means不能检测非球面类别的数据分布，DBSCAN必须指定一个密度阈值，CFDP通过对两种方法的改善，选择每个区域密度最大值，根据密度选择周围点的归属。

核心思想

  1. 求出每个点的密度ρ_i(多种定义方法)

• k近邻均值倒数
  $$\rho_i = \frac{k}{\displaystyle \sum_{j=1}^k d_{ij}} \ , \ d_{i1} \leq d_{i2} \leq \cdots \leq d_{in}$$
• 高斯核相似度
  $$\rho_i = \underset{d_{ij} \leq d_c}{\sum}exp[-(\frac{d_{ij}}{d_c})^2]$$
• 周围点的个数
  $$\rho_i = \sum_{j=1}^n {\chi(d_{ij}-d_c)} \ , \ \chi(x)= \begin{cases} 1, & x<0 \[2ex] 0, & otherwise \end{cases} \ , \ 其中d_c为截断距离$$

  2. 密度从大到小排序，并求出最大密度ρ_max
$$\rho_{x_1} \ge \rho_{x_2} \ge \cdots \ge \rho_{x_n} \ , \ \rho_{max} = \rho_{x_1} $$

• d_ij:原序列i，j样本的距离
• d(x_i,x_j):密度排序后，x_i和x_j样本的距离

  3. 求出每个点的距离δ_i
  δ_i：到密度大于i的最近点j的距离dist(ij)
$$\delta_{x_i} = \begin{cases} \underset{j<i}{min}\ d(x_i,x_j) & i \ge 2 \[2ex] \underset{j \ge 2}{\max}\ \delta_{x_j} & i=1 \end{cases} $$

  4. 画出ρ-δ图，找到离群点(代表每一类的中心)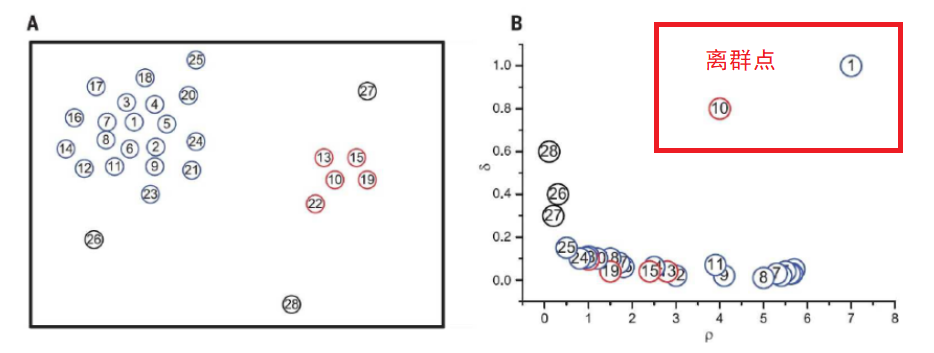

  5. 按密度从大到小归属于距离最近点的类别
$$x_i \in C_k \ , \ 其中k=\underset{j<i \ , \ x_j \in C_k}{arg \ min}\ d(x_i,x_j)$$

  6. 定义两类之间的最小距离d₀
  两类的最小距离：所有样本之间距离从小到大排序后第2%个称两类的最小距离。

  7. 定义边缘点，求出边缘点最大密度ρ_b
  边缘点：在k类数据到非k类数据的最小距离小于dist₀的点，称为k类数据的边缘点。
$$E = {i | d_{ij}<dist_0 , \forall i \in C_k , j \in \overline{C_k} }$$
$$\rho_b = \underset{i \in E}{\max}\ \rho_i$$

  8. 判断噪声点
  噪声点：将k类中密度小于ρ_b的所有数据记为噪声。
$$N={i | \rho_i<\rho_b , \forall i \in C_k }$$

算法流程

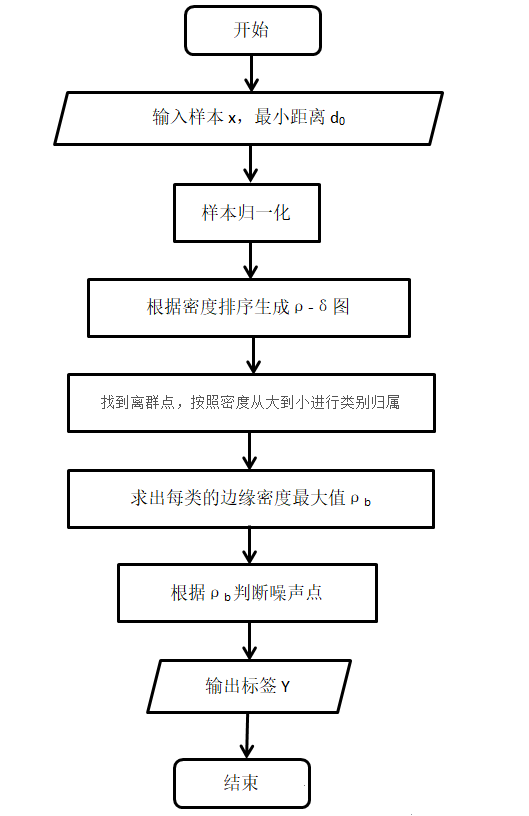
代码实战

代码中所用数据集可以查看相关文档，数据集(Data Set)

CFDP_main.m

clear;clc;close all;
load('..\\cluster_line.mat');
%输入x的矩阵
x=data;
randIndex = randperm(size(x,2));
x=x(:,randIndex);
%样本数
sample_num=size(x,2);
%判断密度时检测周围点的个数
k=round(sample_num/10);
%特征数目
feat_num=size(x,1);
%尺度缩放到0-1
x_scale=zeros(size(x));
for i=1:feat_num
    x_scale(i,:)=(x(i,:)-min(x(i,:)))/(max(x(i,:))-min(x(i,:)));
end
[y,density_max]=CFDP_classify(x_scale,sample_num,k);
% 如果数据的特征是二维的，可以绘图表示
if feat_num==2
    CFDP_display(x,y,sample_num,density_max)
else
    disp('The Feature Is Not Two-Dimensional');
end

CFDP_classify.m

function [y,density_max]=CFDP_classify(x_scale,sample_num,k)
y=zeros(1,sample_num);
%p为每个样本的密度
p=zeros(1,sample_num);
%deta为高密度距离
deta=zeros(1,sample_num);
%distance(i,j)代表第i个样本到第j个样本的距离
distance=zeros(sample_num);
%利用k近邻均值定义密度较好，不会出现很多密度相同的点。如果采用半径内个数的定义方法，可能一块区域会出现很多的类别
for i=1:sample_num
    distance(i,:)=sum((x_scale-repmat(x_scale(:,i),1,sample_num)).^2);
    temp=sort(distance(i,:));
    p(i)=k./sum(distance(i,distance(i,:)<=temp(k)));
end
for i=1:sample_num
    temp=find(p>p(i));
    %如果有多个最大点
    if isempty(temp)
        deta(i)=distance(i,find(p==max(p),1));
    else
        %找到密度大于该点的且距离该点最近的点
        tem=find(distance(i,p>p(i))==min(distance(i,p>p(i))),1);
        deta(i)=distance(i,temp(tem));
    end
end
%密度最大点赋值无穷   
deta(find(p==max(p),1))=1;
p_judge=max(p)/5;
deta_judge=0.1;
%获取类别的中心
center_loc=p>p_judge&deta>deta_judge;
%找到类别中心所在位置
density_max=find(center_loc);
%将p和deta较大的值作为新的聚类中心
y(center_loc)=1:sum(center_loc);
%对密度从大到小排序
[~,density_loc]=sort(p,'descend');
%将某点划分到密度大于该点并且距离该点最近的一类
for i=2:sample_num
    if y(density_loc(i))==0
        temp=density_loc(1:i-1);
        y(density_loc(i))=y(temp(find(distance(density_loc(i),temp)==min(distance(density_loc(i),temp)),1)));
    end
end
%定义两类之间的最小距离
distance_temp=distance.*triu(ones(sample_num));
temp=sort(distance_temp(distance_temp>0));
%取出前%2的距离作为最小距离
dc=temp(round(length(temp)/50));
for i=1:sum(center_loc)
    %得到边缘点
    edge= min(distance(y==i,y~=i),[],2)<dc;
    if ~(isempty(edge)||isequal(edge,zeros(length(find(y==i)),1)))
        tem=find(y==i);
        %得到边缘区域密度最大的值
        pb=max(p(tem(edge)));
        %将密度小于该最大值的点作为噪声点
        y(tem(p(y==i)<=pb))=0;
    end
end

CFDP_display.m

function CFDP_display(x,y,sample_num,density_max)
color_bar=zeros(length(density_max),3);
hold on;
for i=1:length(density_max)
    color_bar(i,:)=[rand(1),rand(1),rand(1)];
end
for i=1:sample_num
    if y(i)==0
        plot(x(1,i),x(2,i),'ko');
    else
        if ismember(i,density_max)
            plot(x(1,i),x(2,i),'color',color_bar(y(i),:),'marker','*');
        else
            plot(x(1,i),x(2,i),'color',color_bar(y(i),:),'marker','o');
        end
    end
end
hold off;

实验结果

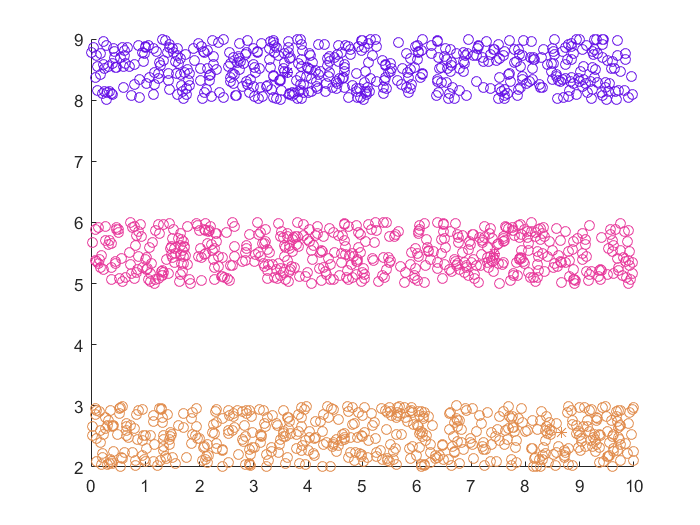
性能比较

• 优点：
  • 对噪声数据不敏感
  • 不依赖初始数据点的选择
  • 可以完成任意形状的聚类
• 缺点：
  • 离群点的确定非常复杂
  • 算法复杂，分类速度较慢
  • 对于高维数据，距离的度量并不是很好
  • 不适合数据集整体密度基本相同的情况