谱聚类方法

原理解读

Spectral Clustering:是一种基于图论的聚类算法，第一步是构图：将数据集中的每个对象看做空间中的点V，将这些点之用边E连接起来，距离较远的两个点之间的边权重值较低、距离较近的两个点之间的边权重值较高，这样就构成了一个基于相似度的无向权重图G(V,E)。第二步是切图：按照一定的切边规则将图切分为不同的子图，规则是使子图内的边权重和尽可能大，不同子图间的边权重和尽可能小，从而达到聚类目的。

核心思想

1. 邻接矩阵W的构建
$$w_{ij}=\begin{cases}exp(-\frac{\lVert x_i-x_j \rVert ^2}{2 \sigma ^2}) & i \neq j \\[2ex] 0 & i=j \end{cases}$$

2. 度矩阵W的构建
$$d_{ij}=\begin{cases}0 & i \neq j \\[2ex] \displaystyle \sum_{j=1} w_{ij} & i=j \end{cases}$$

3. 目标函数

权重切图
$$W(A,B)=\displaystyle \sum_{i \in A, j \in B} w_{ij}$$
Ncut切图
\begin{align}
Ncut(A_1,A_2, \cdots ,A_n) &=\displaystyle \sum_{i=1}^n \frac{W(A_i, \overline {A_i})}{\displaystyle \sum_{j \in A_i} \displaystyle \sum_{k=1} w_{jk}} \\
&=\underset{F}{\underbrace{arg\ min}}\ {tr(F^TD^{-1/2}LD^{-1/2}F)} \ , \ s.t. \ H^TDH=\mathrm{I}
\end{align}

4. 求标准化拉普拉斯矩阵
$$L_{sym}=D^{-1/2}LD^{-1/2}=D^{-1/2}(D-W)D^{-1/2}$$

5. 取前K个特征值对应的特征向量

6. 用K-Means对归一化的特征向量进行分类

7. 一个便于理解的实例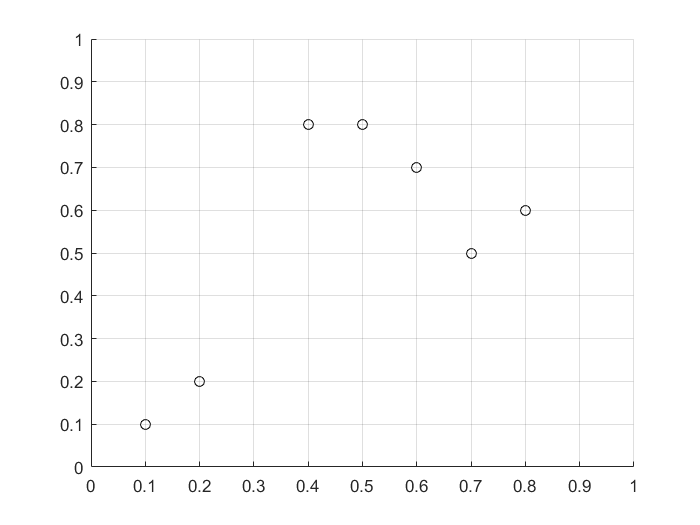
SPECTRAL
$$x=\begin{bmatrix} 0.7 & 0.8 & 0.1 & 0.4 & 0.2 & 0.5 & 0.6 \\ 0.5 & 0.6 & 0.1 & 0.8 & 0.2 & 0.8 & 0.7 \end{bmatrix}$$

$$w=\begin{bmatrix} 0 & 0.990 & 0.771 & 0.914 & 0.844 & 0.937 & 0.975 \\ 0.990 & 0 & 0.691 & 0.905 & 0.771 & 0.937 & 0.975 \\ 0.771 & 0.691 & 0 & 0.748 & 0.990 & 0.723 & 0.737 \\ 0.914 & 0.905 & 0.748 & 0 & 0.819 & 0.995 & 0.975 \\ 0.844 & 0.771 & 0.990 & 0.819 & 0 & 0.799 & 0.815 \\ 0.937 & 0.937 & 0.723 & 0.995 & 0.799 & 0 & 0.990 \\ 0.975 & 0.975 & 0.737 & 0.975 & 0.815 & 0.990 & 0 \end{bmatrix}$$

$$d=\begin{bmatrix} 5.43 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 5.27 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 4.66 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 5.36 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 5.04 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 5.38 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 5.47 \end{bmatrix}$$

$$L_{sym}=\begin{bmatrix} 1 & -0.185 & -0.153 & -0.169 & -0.161 & -0.173 & -0.179 \\ -0.185 & 1 & -0.139 & -0.170 & -0.150 & -0.176 & -0.182 \\ -0.153 & -0.139 & 1 & -0.150 & -0.204 & -0.144 & -0.146 \\ -0.169 & -0.170 & -0.150 & 1 & -0.158 & -0.185 & -0.180 \\ -0.161 & -0.150 & -0.204 & -0.158 & 1 & -0.153 & -0.155 \\ -0.173 & -0.176 & -0.144 & -0.185 & -0.153 & 1 & -0.183 \\ -0.179 & -0.182 & -0.146 & -0.180 & -0.155 & -0.183 & 1 \end{bmatrix}$$

$$feature\_value=\begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1.080 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1.159 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1.205 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1.183 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1.187 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1.186 \end{bmatrix}$$

$$feature\_vector=\begin{bmatrix} -0.385 & -0.141 & 0.535 & -0.004 & 0.371 & 0.534 & -0.349 \\ -0.379 & -0.302 & 0.470 & -0.040 & 0.042 & -0.691 & 0.249 \\ -0.357 & 0.642 & -0.005 & -0.675 & -0.031 & -0.033 & 0.051 \\ -0.383 & -0.178 & -0.575 & -0.004 & 0.246 & -0.299 & -0.584 \\ -0.371 & 0.558 & 0.010 & 0.736 & -0.036 & -0.053 & 0.070 \\ -0.383 & -0.261 & -0.400 & -0.019 & 0.264 & 0.314 & 0.676 \\ -0.387 & -0.256 & -0.034 & -0.017 & -0.853 & 0.213 & -0.104 \end{bmatrix}$$
取最小的两个特征值对应的特征向量可得：
$$feature\_vector=\begin{bmatrix} -0.385 & -0.141 \\ -0.379 & -0.302 \\ -0.357 & 0.642 \\ -0.383 & -0.178 \\ -0.371 & 0.558 \\ -0.383 & -0.261 \\ -0.387 & -0.256 \end{bmatrix}$$
特征向量按行归一化：
$$feature\_vector=\begin{bmatrix} -0.939 & -0.344 \\ -0.782 & -0.623 \\ -0.486 & 0.874 \\ -0.907 & -0.422 \\ -0.553 & 0.833 \\ -0.827 & -0.563 \\ -0.834 & -0.552 \end{bmatrix}$$

此时7个点变成了7个行向量，从第二维可以明显看出：${x_1,x_2,x_4,x_6,x_7} \in A_1\ ,\ {x_3,x_5} \in A_2$

在本例中，点的坐标是二维的，提取特征后也是二维的，给大家的感觉是不如直接使用K-Means，但是如果输入特征是n维，就可以看出差异了。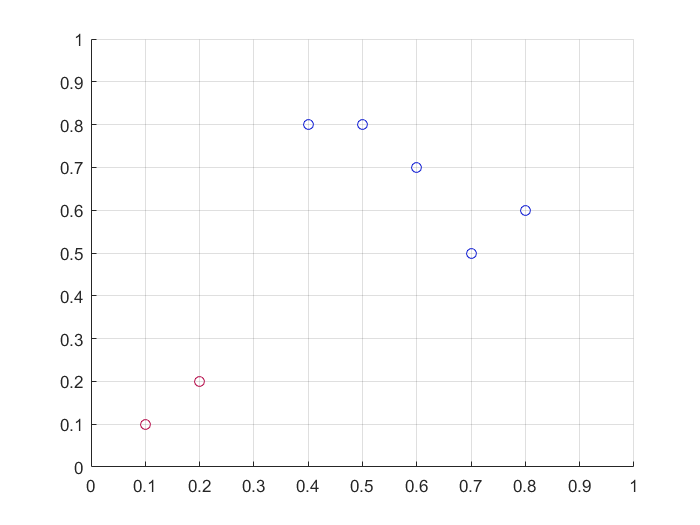
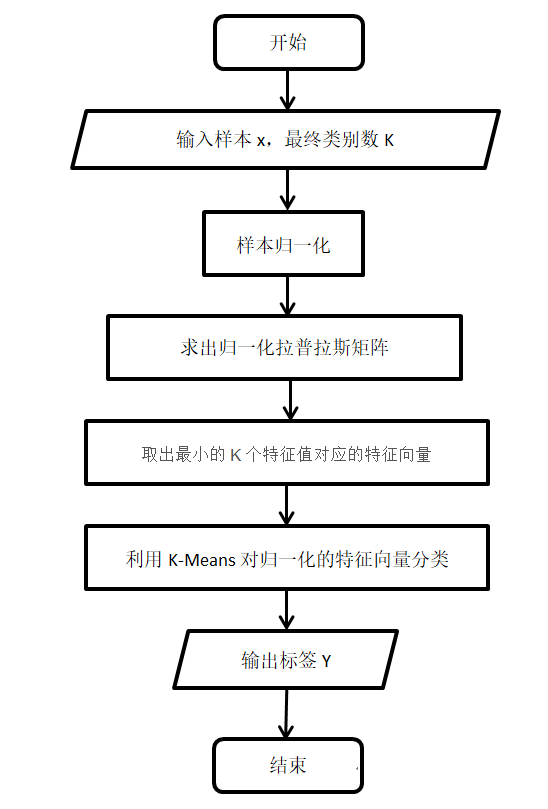
SPECTRAL

算法流程

SPECTRAL

代码实战

代码中所用数据集可以查看相关文档，数据集(Data Set)

SPECTRAL_main.m

clear;clc;close all;
load('..\\\\cluster_mixture.mat');
%输入x的矩阵
x=data;
randIndex = randperm(size(x,2));
x=x(:,randIndex);
%希望划分的类别数
class_num=3;
%样本数
sample_num=size(x,2);
%特征数目
feat_num=size(x,1);
%尺度缩放到0-1
x_scale=zeros(size(x));
for i=1:feat_num
    x_scale(i,:)=(x(i,:)-min(x(i,:)))/(max(x(i,:))-min(x(i,:)));
end
y=SPECTRAL_classify(x_scale,sample_num,class_num);
%如果数据的特征是二维的，可以绘图表示
if feat_num==2
    SPECTRAL_display(x,y,sample_num,class_num);
else
    disp('The Feature Is Not Two-Dimensional');
end

SPECTRAL_classify.m

function y=SPECTRAL_classify(x_scale,sample_num,class_num)
%w为邻接矩阵
w=zeros(sample_num);
for i=1:sample_num
    w(i,:)=exp(-sum((x_scale-repmat(x_scale(:,i),1,sample_num)).^2)/2);
    w(i,i)=0;
end
%D为度矩阵
d=diag(sum(w,2));
%标准化拉普拉斯矩阵
l=d^(-0.5)*(d-w)*d^(-0.5);
%求特征向量和特征值
[feat_vector,feat_value_temp]=eig(l);
feat_value=diag(feat_value_temp);
temp=sort(feat_value);
loc=feat_value<=temp(class_num);
%求出最小的class_num个特征向量
class_feat_vector=feat_vector(:,loc);
%特征向量归一化
class_feat_vector=class_feat_vector./repmat(sqrt(sum(class_feat_vector.^2,2)),1,class_num);
%利用kmeans进行分类
y=SPECTRAL_kmeans(class_feat_vector',sample_num,class_num);

SPECTRAL_display.m

function SPECTRAL_display(x,y,sample_num,class_num)
color_bar=zeros(class_num,3);
hold on;
for i=1:class_num
    color_bar(i,:)=[rand(1),rand(1),rand(1)];
end
for i=1:sample_num
    %绘制数据集，用o表示
    plot(x(1,i),x(2,i),'color',color_bar(y(i),:),'marker','o');
end
hold off;

SPECTRAL_kmeans.m

function y=SPECTRAL_kmeans(class_feat_vector,sample_num,class_num)
%类别中心位置
loc_center=class_feat_vector(:,1:class_num);
%设置迭代次数
k=0;
while 1
    %初始化最新的分类中心
    loc_center_new=zeros(size(loc_center));
    distance=zeros(class_num,sample_num);
    %distance为每一个样本到每一类的距离
    for i=1:class_num
        distance(i,:)=sum((class_feat_vector-repmat(loc_center(:,i),1,sample_num)).^2);
    end
    %求出每个样本到哪一类最近
    [~,y]=min(distance);
    %更新分类中心
    for i=1:class_num
        loc_center_new(:,i)=sum(class_feat_vector(:,y==i),2)/sum(y==i);
    end
    %如果分类中心和上一次分类中心相等则分类完毕
    if isequal(loc_center_new,loc_center)
        break;
    %否则继续分类
    else
        loc_center=loc_center_new;
        k=k+1;
        %如果分类次数达到1000仍然没有结束，则强制分类结束
        if k>=1000
            break;
        end
    end
end

实验结果

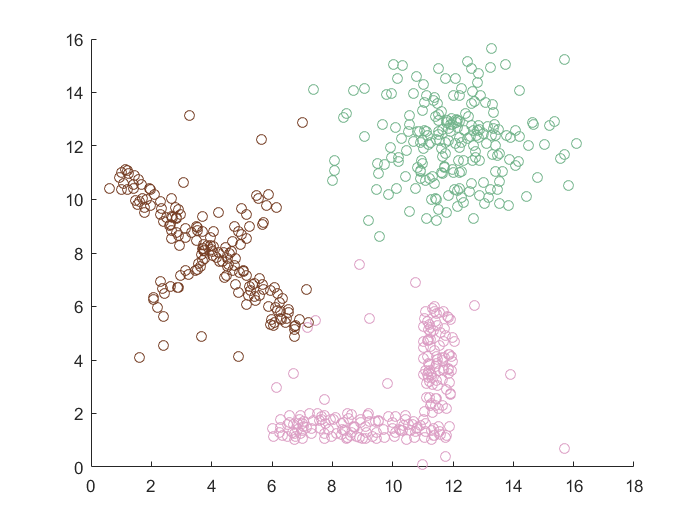
SPECTRAL

性能比较

优点：
- 不依赖初始数据点的选择
- 使用了降维技术，适合于高维数据的聚类
- 建立在谱图理论，能在大部分形状聚类，收敛于全局最优解

缺点：

难以对圆形数据聚类
对噪声数据非常敏感
需要在测试前知道类别的个数