高斯混合模型聚类(GMM)

高斯混合模型聚类方法

原理解读

  GMM(Gaussian Mixture Model,):是一个将事物分解为若干的基于高斯概率密度函数（正态分布曲线）形成的模型，混合高斯分布( MoG )由多个混合成分组成，每一个混合成分对应一个高斯分布。当聚类问题中各个类别的尺寸不同、聚类间有相关关系的时候，往往使用 MoG 更合适。对一个样本来说， MoG 得到的是其属于各个类的概率(通过计算后验概率得到)，而不是完全的属于某个类，这种聚类方法被成为软聚类。一般说来， 任意形状的概率分布都可以用多个高斯分布函数去近似，因而，MoG 的应用也比较广泛。

步骤分析

  1. 选择高斯模型个数K，初始化参数

  2. 根据贝叶斯定理，求出z_j的后验分布概率
$$p(z_j=i | x_j) = \frac{\alpha_i \cdot p(x_j | \mu_i , \Sigma_i)}{\displaystyle \sum_{l=1}^k \alpha_l \cdot p(x_j | \mu_l , \Sigma_l)}$$

  3. 使用EM算法进行迭代

• 计算均值向量：
  $$\mu_i ‘=\frac{\displaystyle \sum_{j=1}^m p(z_j=i | x_j) \cdot x_j}{\displaystyle \sum_{j=1}^m p(z_j=i | x_j)}$$

• 计算协方差矩阵：
  $$\Sigma_i ‘=\frac{\displaystyle \sum_{j=1}^m p(z_j=i | x_j) \ (x_j - \mu_i ‘) \ (x_j - \mu_i ‘)^T}{\displaystyle \sum_{j=1}^m p(z_j=i | x_j)}$$

• 计算混合系数：
  $$\alpha_i ‘=\frac{\displaystyle \sum_{j=1}^m p(z_j=i | x_j)}{m}$$

  4. 重复步骤1，2，直到满足某个终止条件

  5. 定义高斯混合分布
  根据所求得的均值向量，协方差矩阵和混合系数可以定义如下函数：
$$p(x)=\displaystyle \sum_{l=1}^k \alpha_i \cdot p(x | \mu_i , \Sigma_i) \ , \ s.t. \displaystyle \sum_{l=1}^k \alpha_i=1$$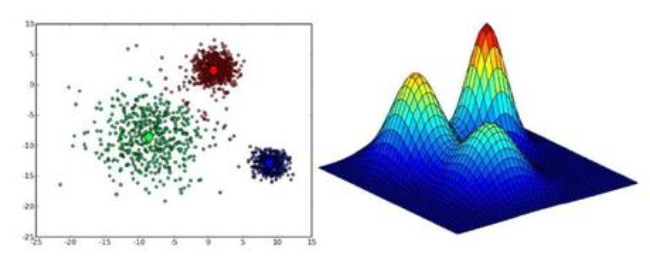

  6. 对样本进行标记
$$\lambda_j=\underset{i \in { 1,2, \cdots ,k}}{arg\ max} \ p(z_j=i | x_j)$$

算法流程

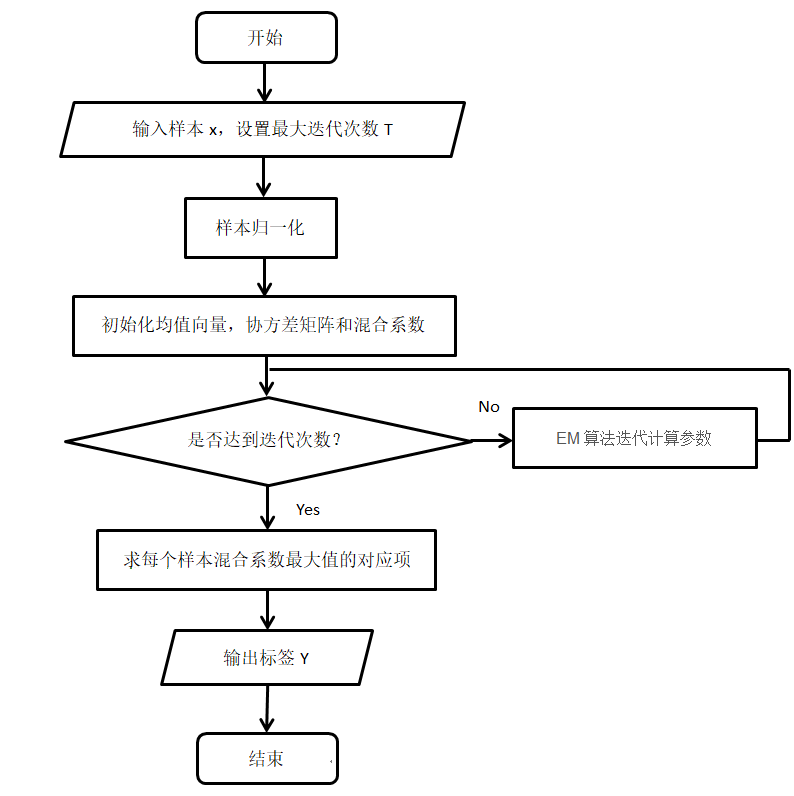
代码实战

代码中所用数据集可以查看相关文档，数据集(Data Set)

GMM_main.m

clear;clc;close all;
load('..\\cluster_mixture.mat');
%输入x的矩阵
x=data;
%样本数
sample_num=size(x,2);
%混合高斯个数
class_num=3;
%特征数目
feat_num=size(x,1);
%尺度缩放到0-1
x_scale=zeros(size(x));
for i=1:feat_num
    x_scale(i,:)=(x(i,:)-min(x(i,:)))/(max(x(i,:))-min(x(i,:)));
end
y=GMM_classify(x_scale,sample_num,class_num,feat_num);
% 如果数据的特征是二维的，可以绘图表示
if feat_num==2
    GMM_display(x,y,sample_num,class_num);
else
    disp('The Feature Is Not Two-Dimensional');
end

GMM_classify.m

function y=GMM_classify(x_scale,sample_num,class_num,feat_num)
%初始化均值向量,协方差矩阵，混合系数
a=ones(1,class_num)/class_num;
u=zeros(feat_num,class_num);
sigma=zeros(feat_num,feat_num,class_num);
randIndex = randperm(size(x_scale,2));
u(:,1:class_num)=x_scale(:,randIndex(1:class_num));
for i=1:class_num
    sigma(:,:,i)=eye(feat_num)/10;
end
for t=1:50
    %判断sigma是否正定
    if sum(sum(sum(isnan(sigma))))>0||sum(sum(sum(isinf(sigma))))>0
        break;
    end
    pm_x=zeros(1,sample_num);
    %计算每个样本的全概率
    for i=1:sample_num
        tem=0;
        for j=1:class_num
            tem=tem+a(j)*mvnpdf(x_scale(:,i), u(:,j), sigma(:,:,j));
        end
        pm_x(i)=tem;
    end
    %计算第i个样本属于第j类的后验概率
    pm=zeros(sample_num,class_num);
    for i=1:sample_num
        for j=1:class_num
            pm(i,j)=a(j)*mvnpdf(x_scale(:,i), u(:,j), sigma(:,:,j))/pm_x(i);
        end
    end
    %计算均值向量,协方差矩阵，混合系数
    for i=1:class_num
        sum_pm=sum(pm(:,i));
        u(:,i)=sum(repmat(pm(:,i)',feat_num,1).*x_scale,2)/sum_pm;
        for j=1:sample_num
            sigma(:,:,i)=sigma(:,:,i)+pm(j,i)*(x_scale(:,j)-u(:,i))*(x_scale(:,j)-u(:,i))';
        end
        sigma(:,:,i)=sigma(:,:,i)/sum_pm;
        a(i)=sum_pm/sample_num;
    end
end
%把每个样本中混合系数最大的一个类别作为其标签
[~,y]=max(pm,[],2);

GMM_display.m

function GMM_display(x,y,sample_num,class_num)
figure;
hold on;
color_bar=zeros(class_num,3);
for i=1:class_num
    color_bar(i,:)=[rand(1),rand(1),rand(1)];
end
for i=1:sample_num
    if y(i)==0
        %画出噪声点，用*表示
        plot(x(1,i),x(2,i),'k*')
    else
        %画出每一类的样本数据，用o表示
        plot(x(1,i),x(2,i),'color',color_bar(y(i),:),'marker','o');
    end
end
hold off;

实验结果

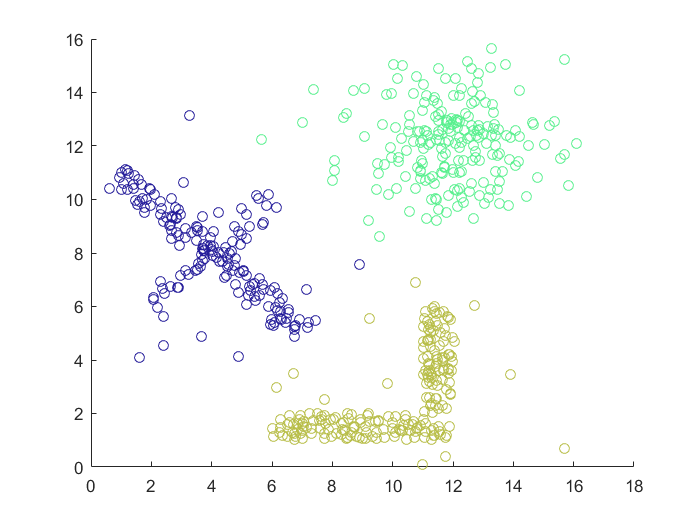
性能比较

• 优点：
  • 可以完成大部分形状的聚类
  • 大数据集时，对噪声数据不敏感
  • 对于距离或密度聚类，更适合高维特征
• 缺点：
  • 计算复杂，速度较慢
  • 难以对圆形数据聚类
  • 需要在测试前知道类别的个数
  • 初始化参数会对聚类结果产生影响