测试函数(Test Function)

测试函数说明

原理介绍

  Test Function:对于全局最优解来说，测试函数的选择是至关重要的，测试函数的好坏往往可以体现出搜索算法的优劣。有时性能一般的算法在某个特定的函数下发挥的很好，但是在别的函数下就很难搜索到全局最优解。因此我们需要设计各种测试函数，从搜索效率，搜索精度，适应程度多个方面综合比较各个算法，只有这样，在今后的使用中才能得心应手。

代码实战

Function_one.m

clear;clc;close all;
f=@(x)x.*sin(sqrt(abs(x)));
x=-5000:1:5000;
y=f(x);
plot(x,y)

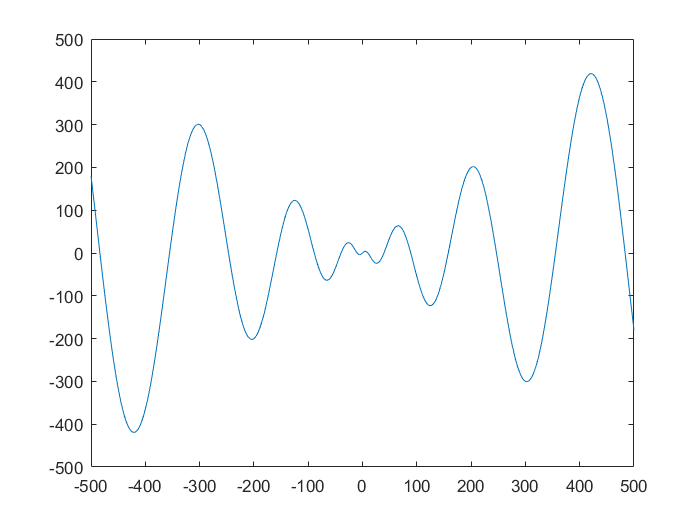
$$f(x)=x \cdot \sin(\sqrt{\lvert x \rvert}) \ , \ x \in [-500,500]$$

$$f(x)_{min}=f(-420.96874592006)=-418.982887272434$$

Function_two.m

clear;clc;close all;
f=@(x)((x+1).*(x+2).*(x+3).*(x+4).*(x+5)+5);
x=-5:0.01:0;
y=f(x);
plot(x,y)

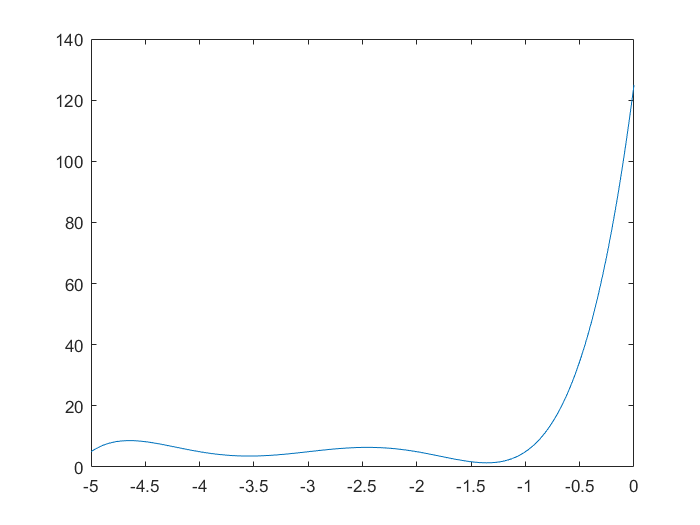
$$f(x)=x \cdot (x+1) \cdot (x+2) \cdot (x+3) \cdot (x+4) \cdot (x+5) + 5 \ , \ x \in [-5,0]$$

$$f(x)_{min}=f(-1.35556713184173)=1.36856779155116$$

Function_three.m

clear;clc;close all;
f=@(x)((x+2).*cos(9*x)+sin(7*x));
x=0:0.01:4;
y=f(x);
plot(x,y)

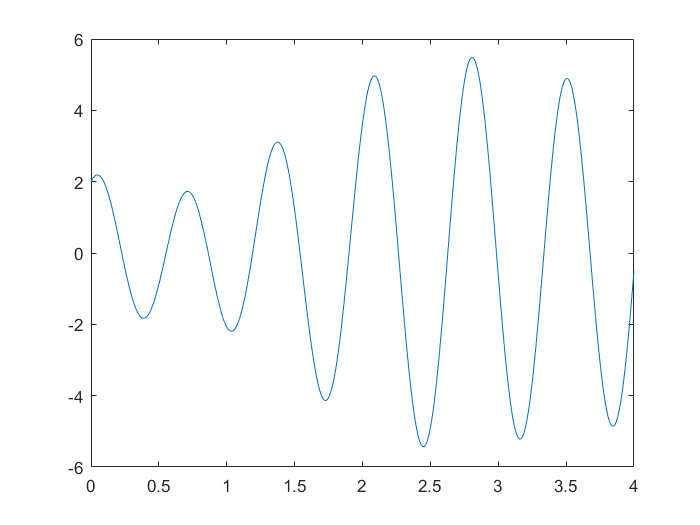
$$f(x)=(x+2) \cdot \cos(9 \ x) + \sin(7 \ x) \ , \ x \in [0,4]$$

$$f(x)_{min}=f(2.44888001781347)=-5.43427465397202$$

Function_four.m

clear;clc;close all;
f=@(x)(5*exp(-0.5*x).*sin(30*x)+exp(0.2*x).*sin(20*x)+6);
x=0:0.01:8;
y=f(x);
plot(x,y)

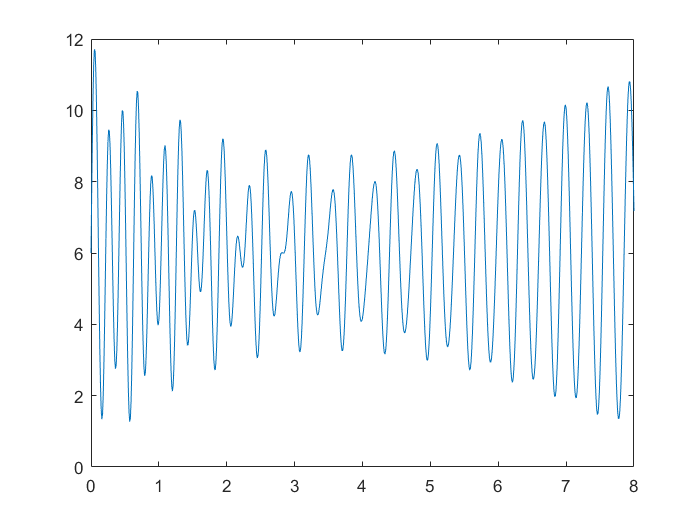
$$f(x)=5 \ e^{-0.5 \ x} \cdot \sin(30 \ x) + e^{0.2 \ x} \cdot \sin(20 \ x) + 6 \ , \ x \in [0,8]$$

$$f(x)_{min}=f(0.5725)=1.2573$$