粒子群算法

背景介绍

PSO(Particle Swarm Optimization):受到飞鸟集群活动的规律性启发，进而利用群体智能建立的一个简化模型。粒子群算法在对动物集群活动行为观察基础上，利用群体中的个体对信息的共享使整个群体的运动在问题求解空间中产生从无序到有序的演化过程，从而获得最优解。

核心思想

1. 随机产生一些粒子

2. 找出所有粒子中适应度最优的粒子g_best
$$g_{best}=\underset{x}{arg \ min} \ f(x)$$

3. 更新每一个粒子的飞行速度
$$v_{i}’=w \cdot v_{i}+c1 \cdot r_{i} \cdot (p_{i}-x_{i})+c2 \cdot s_{i} \cdot (g_{best}-x_{i})$$

4. 获得每个粒子当前位置x_i和该粒子在飞行中到达过的最优位置p_i
$$x_{i}’=x_{i}+v_{i}’$$
$$p_{i}’= \begin{cases} x_{i}’ & f(x_{i}’) < f(p_{i}) \ p_{i} & f(x_{i}’) \ge f(p_{i}) \end{cases}$$

5. 回到步骤2，直到满足某个终止条件

6. 此时粒子集群，粒子群位置为极小值，最小的p为算法的最优解

7. 回到步骤2，直到满足某个终止条件

算法流程

PSO

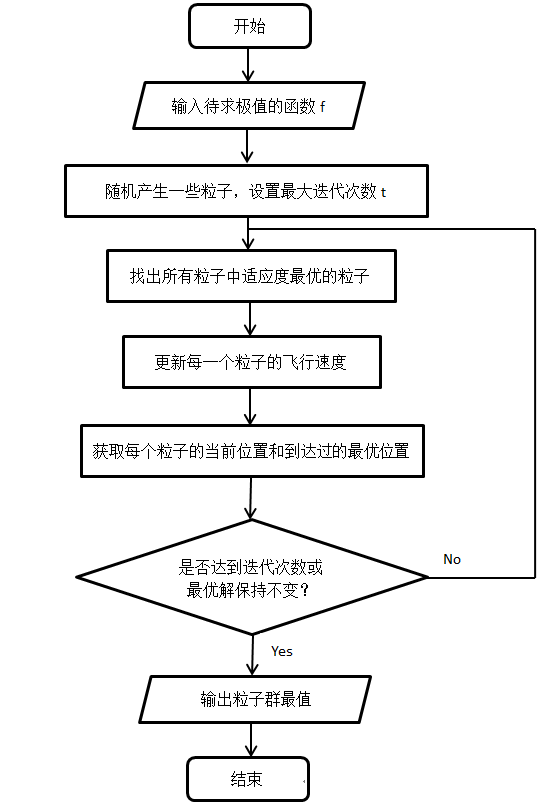
代码实战

代码中所用测试函数可以查看相关文档，测试函数(Test Function)

PSO_main.m

clear;clc;close all;
%自变量取值范围
range_x=[ones(1,1),-ones(1,1)]*500;
%维度
n=size(range_x,1);
%迭代次数
times=100;
%w为惯性权重
w=0.8;
%c1为自身认知权重
c1=1;
%c2为社会认知权重
c2=1;
%粒子群的个数
gn=1000;
%粒子群的初始位置
x=zeros(n,gn);
for k=1:n
    x(k,:)=(rand(1,gn))*(range_x(k,2)-range_x(k,1))+range_x(k,1);
end
%个体极值
p=x;
%v代表粒子的速度
v=zeros(n,gn);
%设置当前最优解
best_value=zeros(1,times);
tic;
for i=1:times
    [solve,gbest]=min(f(x));
    for j=1:gn
        %速度分为3个部分，惯性速度，该点最优和全局最优
        v(:,j)=w*v(:,j)+c1*rand(n,1).*(p(:,j)-x(:,j))+c2*rand(n,1).*(x(:,gbest)-x(:,j));
        x(:,j)=x(:,j)+v(:,j);
        %限制解的范围
        for k=1:n
            if x(k,j)<range_x(k,1)
                x(k,j)=range_x(k,1);
            end
            if x(k,j)>range_x(k,2)
                x(k,j)=range_x(k,2);
            end
        end
        if f(x(:,j))<f(p(:,j))
            p(:,j)=x(:,j);
        end
    end
    best_value(i)=min(f(p));
    if i>5&&abs(best_value(i)-best_value(i-5))<1e-5
        break;
    end
end
time=toc;
disp(['用时：',num2str(time),'秒'])
[mini,index]=min(f(p));
disp(['fmin=',num2str(mini)]);
for k=1:n
    disp(['x',num2str(k),'=',num2str(p(k,index))]);
end
if n==1
    hold on;
    plot(p(index),mini,'ro');
    plot_x=range_x(1):(range_x(2)-range_x(1))/1000:range_x(2);
    plot_y=f(plot_x);
    plot(plot_x,plot_y);
    text((range_x(1)+range_x(2))/2,max(plot_y)+0.1*(max(plot_y)-min(plot_y)),['用时：',num2str(time),'秒']);
    hold off;
end
if n==2
    %所求最小值的函数
    func=@(x1,x2)x1.*sin(sqrt(abs(x1)))+x2.*sin(sqrt(abs(x2)));
    plot_x=range_x(1,1):(range_x(1,2)-range_x(1,1))/1000:range_x(1,2);
    plot_y=range_x(2,1):(range_x(2,2)-range_x(2,1))/1000:range_x(2,2);
    [plot_x,plot_y] =meshgrid(plot_x,plot_y);
    plot_z=func(plot_x,plot_y);
    surf(plot_x,plot_y,plot_z);
    xlabel('x1');
    ylabel('x2');
    zlabel('y');
    hold on;
    plot3(p(1,index),p(2,index),mini,'ko')
    text((range_x(1,1)+range_x(1,2))/2,(range_x(2,1)+range_x(2,2))/2,max(max(plot_z))+0.5*(max(max(plot_z))-min(min(plot_z))),['用时：',num2str(time),'秒']);
    hold off;
end

f.m

function res=f(x)
func=@(x)(x).*sin(sqrt(abs(x)));
res=zeros(1,size(x,2));
for i=1:size(x,1)
    res=res+func(x(i,:));
end

实验结果

PSO
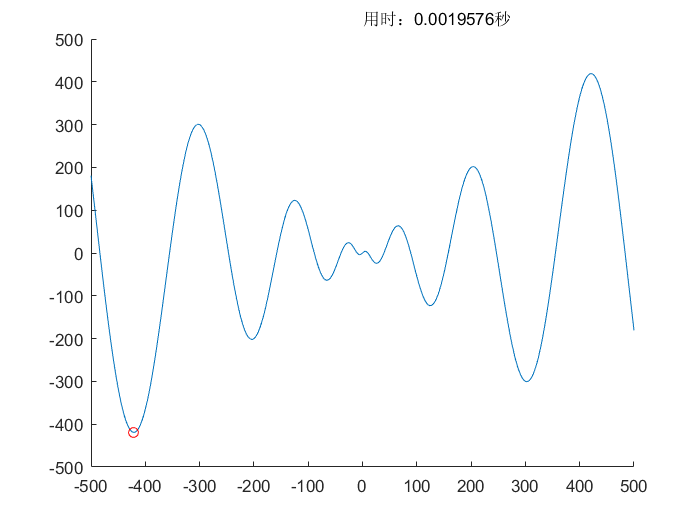
$$f(x)=x \cdot \sin(\sqrt{\lvert x \rvert}) \ , \ x \in [-500,500]$$

$$理论值：f(x)_{min}=f(-420.96874592006)=-418.982887272434$$

$$所求值：f(x)_{min}=f(-420.968750420615)=-418.982887272432$$

性能比较

优点：
- 搜索能力最快
- 从群体出发，具有并行性
- 可用于求解复杂的非线性优化问题

缺点：

受到参数影响较大
存在早熟收敛问题
对初始粒子群的数量有很高的要求