单纯形法(Nelder-Mead)

单纯形法

背景介绍

  Nelder-Mead:单纯形法秉承保证每一次迭代比前一次更优的基本思想，先找出一个基本可行解，看是否是最优解，若不是，则按照一定法则转换到另一改进后更优的基本可行解，再鉴别，若仍不是，则再转换，按此重复进行。因基本可行解的个数有限，故经有限次转换必能得出问题的最优解。

核心思想

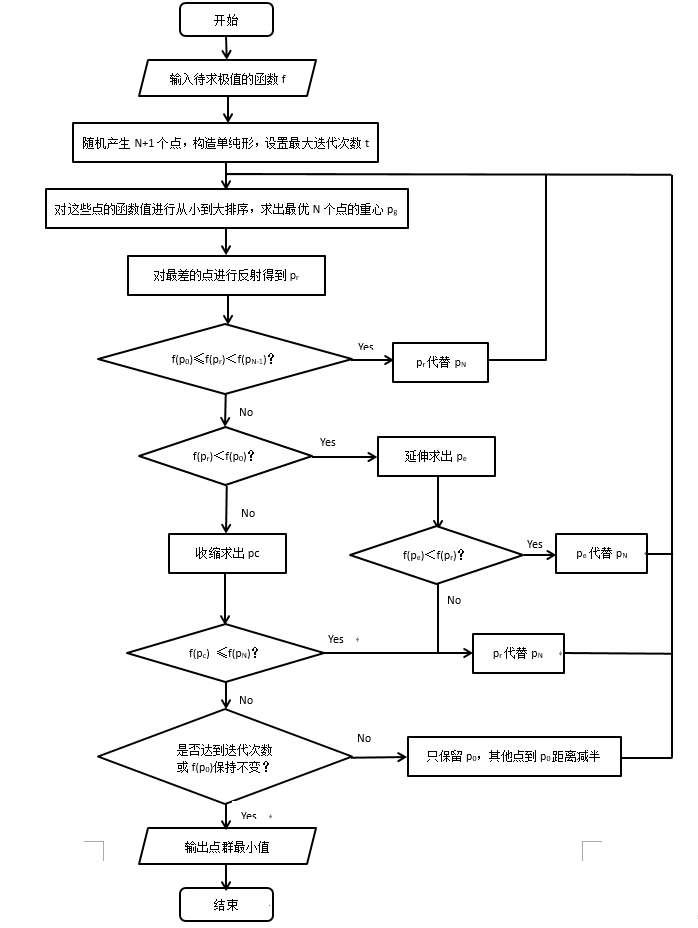
  1. 随机产生N+1个点，构造单纯形，N为所求极值的维度

  2. 对这些点的函数值进行从小到大排序，求出最优N个点的重心p_g
$$f(p_0) \leq f(p_1) \leq \ldots \leq f(p_N)$$
$$p_{g}=\displaystyle \sum_{i=0}^{N-1}\frac {p_{i}}{N}$$

  3. 对最差的点进行反射得到p_r
$$p_{r}=p_{g}+\rho \cdot (p_{g}-p_{N}) \ , \ 其中 \rho 为反射系数$$

  4. 如果f(p₀)≤f(p_r)<f(p_N-1)，p_r代替p_N，回到步骤2

  5. 如果f(p_r)<f(p₀)，说明p_r方向有利于函数值下降
$$p_{e}=p_{g}+ \chi \cdot (p_{r}-p_{g}) \ , \ 其中 \chi 为延伸系数$$

  6. 如果f(p_e)<f(p_r)，p_e代替p_N，否则p_r代替p_N，回到步骤2

  7. f(p_r)≥f(p_N-1)，说明要进行收缩操作
$$p_{c}= \begin{cases} p_{g}+ \gamma \cdot (p_{r}-p_{g}) & f(p_{r}) < f(p_{N}) \ p_{g}+ \gamma \cdot (p_{l}-p_{r}) & f(p_{r}) \ge f(p_{N}) \end{cases} \ , \ 其中 \gamma 为收缩系数$$

  8. 如果f(p_c)≤f(p_N)，p_c代替p_N，回到步骤2

  9. f(p_c)>f(p_r)，只保留p₀，其他点到p₀距离减半，收缩单纯形

  10.如果不满足某个终止条件，回到步骤2

算法流程

代码实战

代码中所用测试函数可以查看相关文档，测试函数(Test Function)

NelderMead_main.m

clear;clc;close all;
%自变量取值范围
range_x=[ones(1,1),-ones(1,1)]*500;
%维度
n=size(range_x,1);
%反射系数rho
rho=1;
%延伸系数
ka1=2;
%收缩系数
ka2=0.5;
%迭代次数
times=100;
%尝试解次数
num=50;
value=zeros(n,num);
tic;
for i=1:num
    %给x赋初值
    x=zeros(n,n+1);
    for k=1:n
        x(k,:)=(rand(1,n+1))*(range_x(k,2)-range_x(k,1))+range_x(k,1);
    end
    best_value=zeros(1,times);
    for j=1:times
        [~,index]=sort(f(x));
        %将小的值排在前面
        x=x(:,index);
        %求重心pg
        xg=sum(x(:,1:end-1),2)/n;
        %进行反射
        xr=xg+rho*(xg-x(:,n+1));
        %判断自变量是否在范围
        for k=1:n
            if xr(k)<range_x(k,1)
                xr(k)=range_x(k,1);
            end
            if xr(k)>range_x(k,2)
                xr(k)=range_x(k,2);
            end
        end
        %如果目标函数值在最好和最坏之间
        if f(xr)>=f(x(:,1))&&f(xr)<f(x(:,n))
            x(:,n+1)=xr;
        %如果新产生的点比最小的点还要小，说明这个方向有利于值的减小
        elseif f(xr)<f(x(:,1))
            %进一步向这个方向延伸
            xe=xg+ka1*(xr-xg);
            for k=1:n
                if xe(k)<range_x(k,1)
                    xe(k)=range_x(k,1);
                end
                if xe(k)>range_x(k,2)
                    xe(k)=range_x(k,2);
                end
            end
            %如果第二次延伸后的点比第一次延伸后产生的点小，则用第二次延伸后的点替换原来最大的点
            if f(xe)<f(xr)
                x(:,n+1)=xe;
            %否则用第一次延伸后的点替换原来最大的点
            else
                x(:,n+1)=xr;
            end
        %如果新产生的点比最小的点还要大
        else
            %如果新产生的点比最大的点小，说明要进行外收缩
            if f(xr)<f(x(:,n+1))
                xc=xg+ka2*(xr-xg);
            %如果新产生的点比最大的点大，说明要进行内收缩
            else
                xc=xg+ka2*(x(:,n+1)-xg);
            end
            %如果无论进行内收缩还是外收缩产生的值都比最大值要小，则替换最大值
            if f(xc)<=f(x(:,n+1))
                x(:,n+1)=xc;
            %%如果无论进行内收缩还是外收缩产生的值都比最大值要大，则缩小范围继续搜索
            else
                for k=2:n+1
                    x(:,k)=(x(:,1)+x(:,k))/2;
                end
            end
        end
        best_value(j)=x(find(f(x)==min(f(x)),1));
        if j>5&&abs(best_value(j)-best_value(j-5))<1e-5
            break;
        end
    end
    value(:,i)=x(:,find(f(x)==min(f(x)),1));
end
time=toc;
disp(['用时：',num2str(time),'秒'])
[mini,index]=min(f(value));
disp(['fmin=',num2str(mini)]);
for k=1:n
    disp(['x',num2str(k),'=',num2str(value(k,index))]);
end
if n==1
    hold on;
    plot(value(index),mini,'ro');
    plot_x=range_x(1):(range_x(2)-range_x(1))/1000:range_x(2);
    plot_y=f(plot_x);
    plot(plot_x,plot_y);
    text((range_x(1)+range_x(2))/2,max(plot_y)+0.1*(max(plot_y)-min(plot_y)),['用时：',num2str(time),'秒']);
    hold off;
end
if n==2
    func=@(x1,x2)x1.*sin(sqrt(abs(x1)))+x2.*sin(sqrt(abs(x2)));
    plot_x=range_x(1,1):(range_x(1,2)-range_x(1,1))/1000:range_x(1,2);
    plot_y=range_x(2,1):(range_x(2,2)-range_x(2,1))/1000:range_x(2,2);
    [plot_x,plot_y] =meshgrid(plot_x,plot_y);
    plot_z=func(plot_x,plot_y);
    surf(plot_x,plot_y,plot_z);
    xlabel('x1');
    ylabel('x2');
    zlabel('y');
    hold on;
    plot3(value(1,index),value(2,index),mini,'ko')
    text((range_x(1,1)+range_x(1,2))/2,(range_x(2,1)+range_x(2,2))/2,max(max(plot_z))+0.5*(max(max(plot_z))-min(min(plot_z))),['用时：',num2str(time),'秒']);
    hold off;
end

f.m

function res=f(x)
func=@(x)(x).*sin(sqrt(abs(x)));
res=zeros(1,size(x,2));
for i=1:size(x,1)
    res=res+func(x(i,:));
end

实验结果

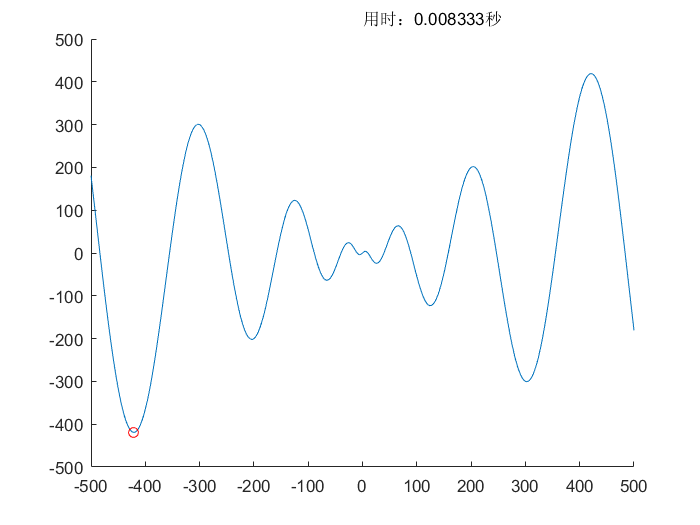
$$f(x)=x \cdot \sin(\sqrt{\lvert x \rvert}) \ , \ x \in [-500,500]$$

$$理论值：f(x)_{min}=f(-420.96874592006)=-418.982887272434$$

$$所求值：f(x)_{min}=f(-420.968746504328)=-418.982887272434$$

性能比较

• 优点：
  • 受到参数影响较小
  • 具有快速随机的搜索能力
  • 可用于求解复杂的非线性优化问题
  • 每次迭代都更接近最优解，精度最高
• 缺点：
  • 算法性能与初始值有关
  • 不适用于多维的最优值求解
  • 可能落入其他的局部最小值