全局搜索
梯度方法，牛顿法，共轭梯度法，拟牛顿法等，能够从初始点出发，产生一个迭代序列。但是很多时候，往往只能收敛到局部极小点。因此为了保证算法能够收敛到全局最小点，需要借助于全局搜索算法来实现。
算法分类
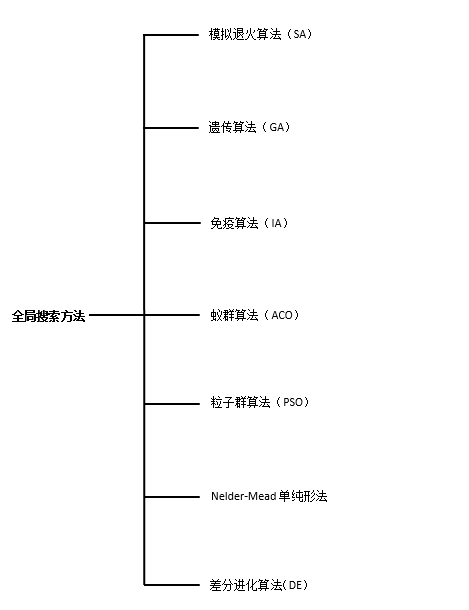
性能比较
所用测试函数可以查看相关文档，测试函数(Test Function)
模拟退火算法(SA)
- 优点：
- 计算过程简单
- 可用于求解复杂的非线性优化问题
- 相比梯度下降，增加了逃离局部最小的可能
- 缺点：
- 参数敏感
- 收敛速度慢
- 执行时间长
- 算法性能与初始值有关
- 可能落入其他的局部最小值
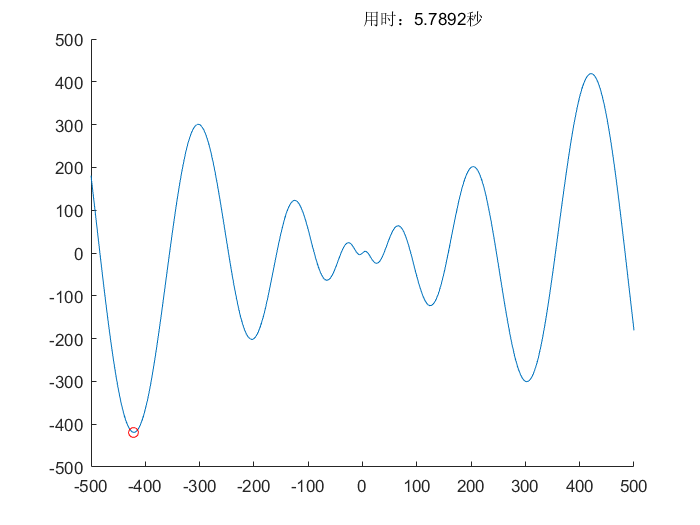
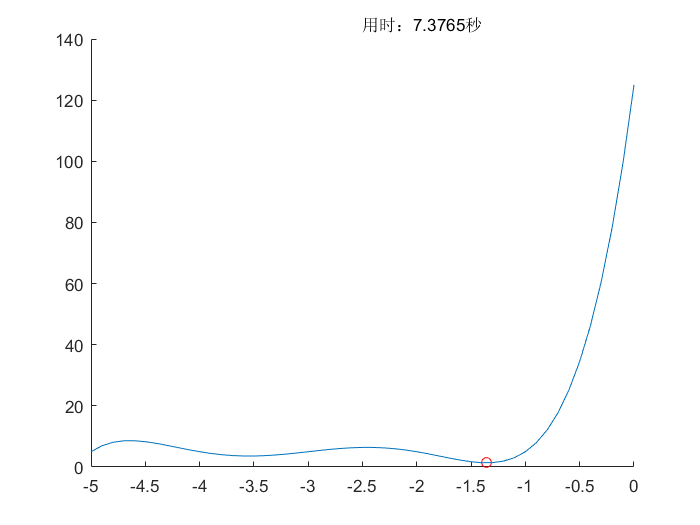
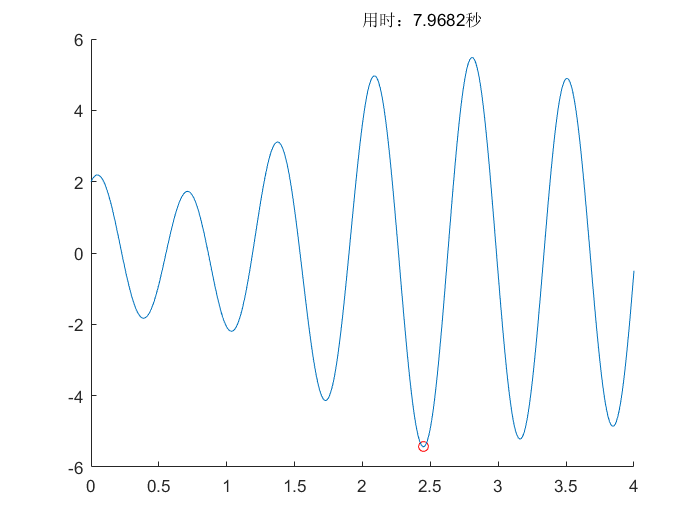
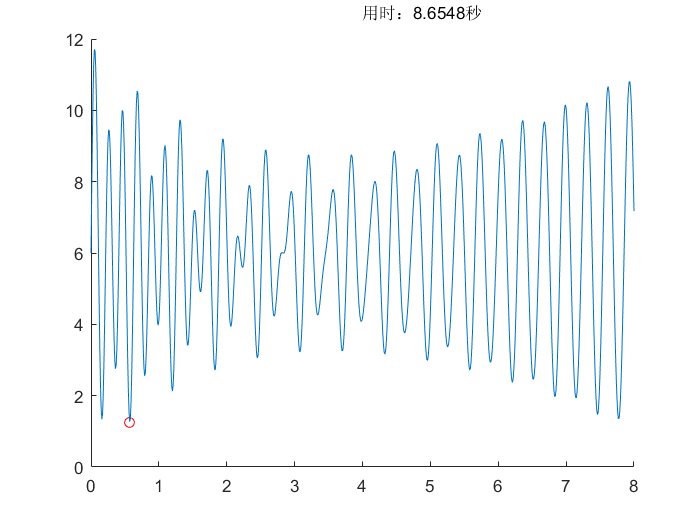
遗传算法(GA)
- 优点：
- 从群体出发，具有并行性
- 可用于求解复杂的非线性优化问题
- 使用概率机制进行迭代，具有随机性
- 具有可扩展性，容易与其他算法结合
- 缺点：
- 受到参数影响较大
- 可能产生早熟收敛问题
- 对问题编码表示较为困难
- 算法对初始种群的选择有一定的依赖性
- 搜索速度比较慢，要得到较精确的解需要较多的训练时间
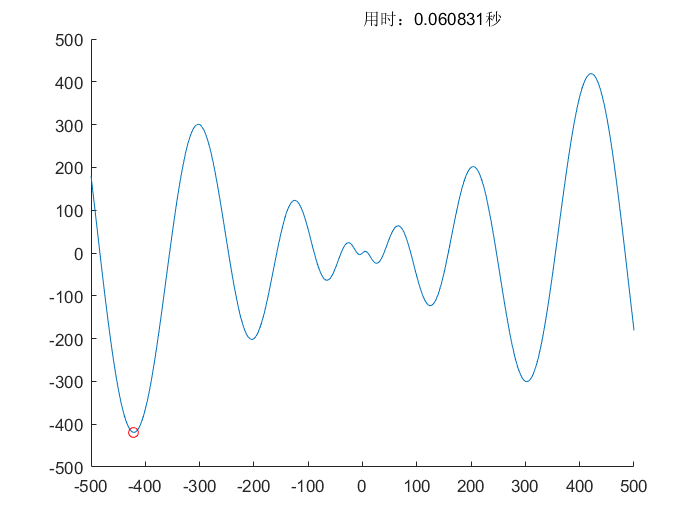
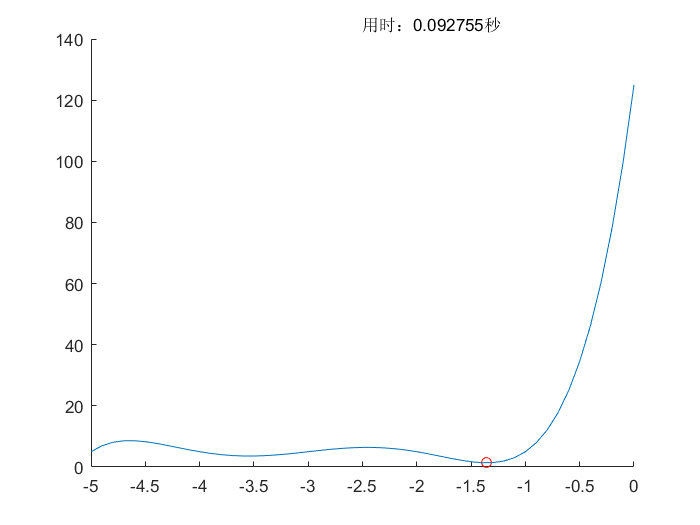
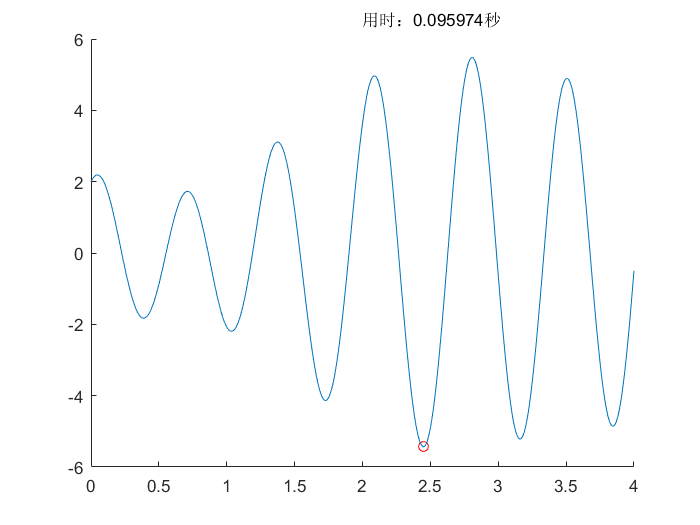
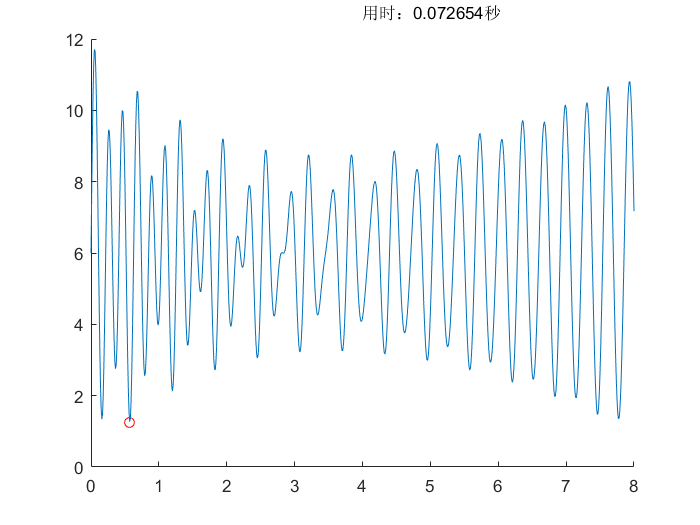
免疫算法(IA)
- 优点：
- 受到参数影响较小
- 解决早熟收敛问题
- 从群体出发，具有并行性
- 对抗体选择的依赖性降低
- 可用于求解复杂的非线性优化问题
- 使用概率机制进行迭代，具有随机性
- 缺点：
- 对问题编码表示较为困难
- 要进行多次免疫应答，因此速度慢于遗传算法
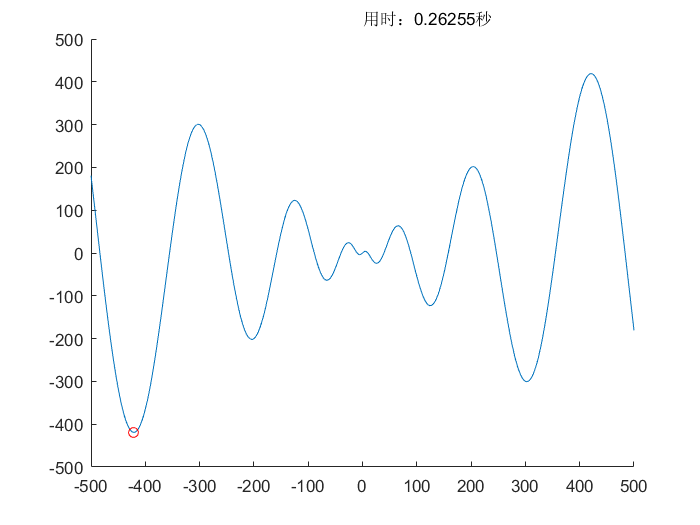
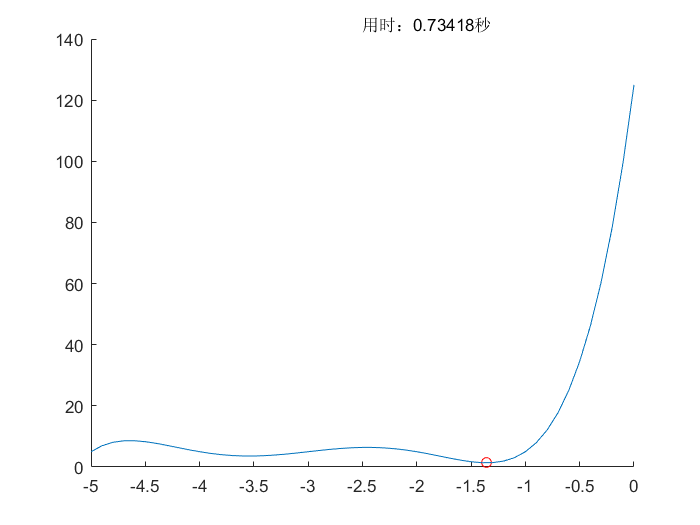
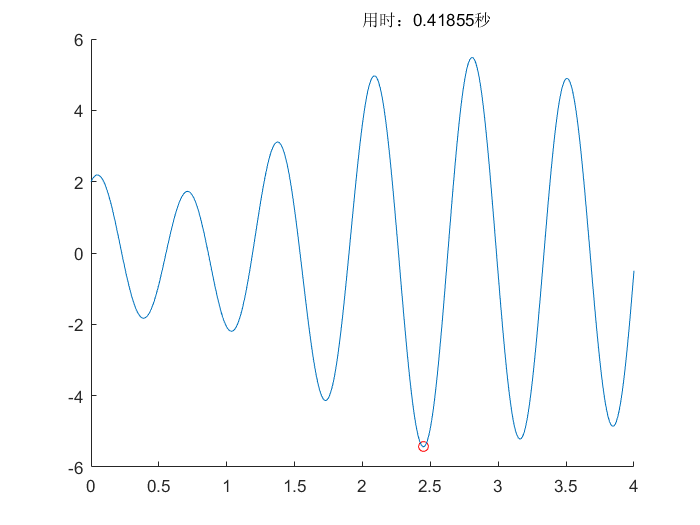
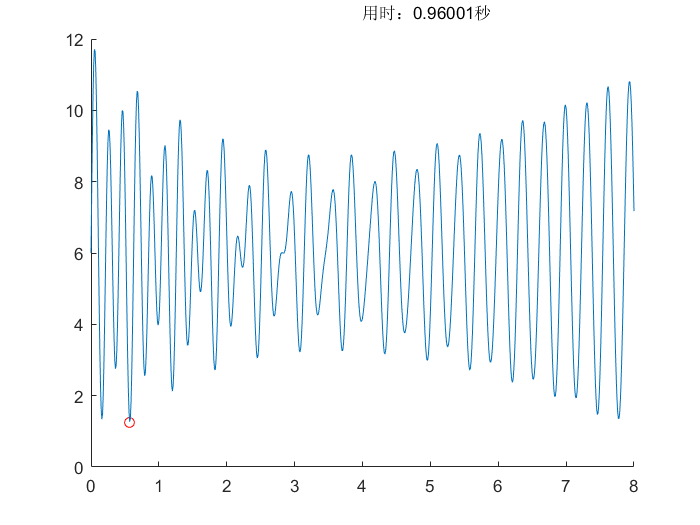
蚁群算法(ACO)
- 优点：
- 搜索速度较快
- 受到参数影响较小
- 从群体出发，具有并行性
- 可用于求解复杂的非线性优化问题
- 具有可扩展性，容易与其他算法结合
- 缺点：
- 对初始蚂蚁的数量有很高的要求
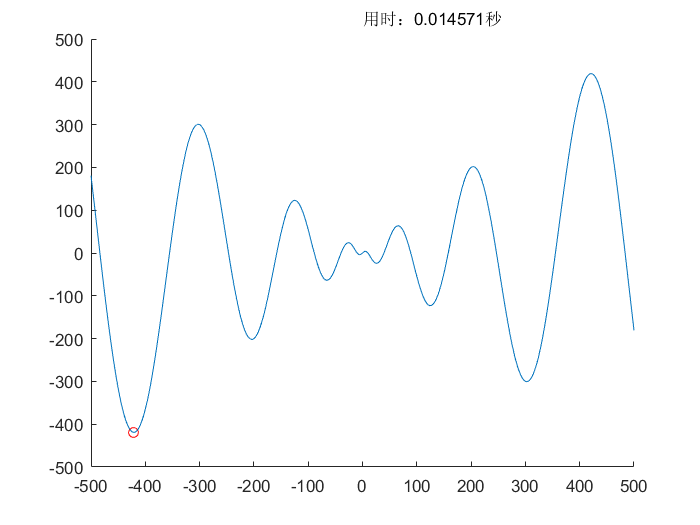
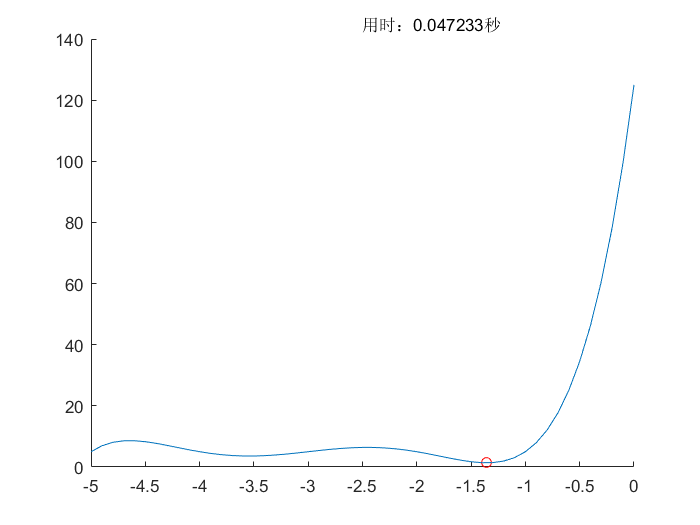
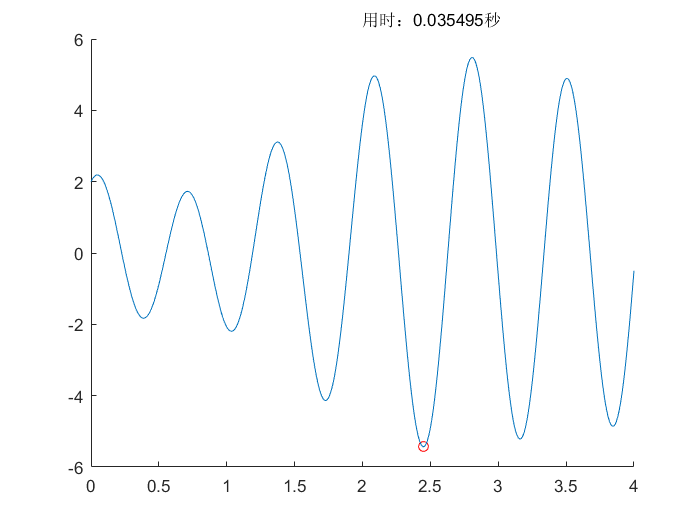
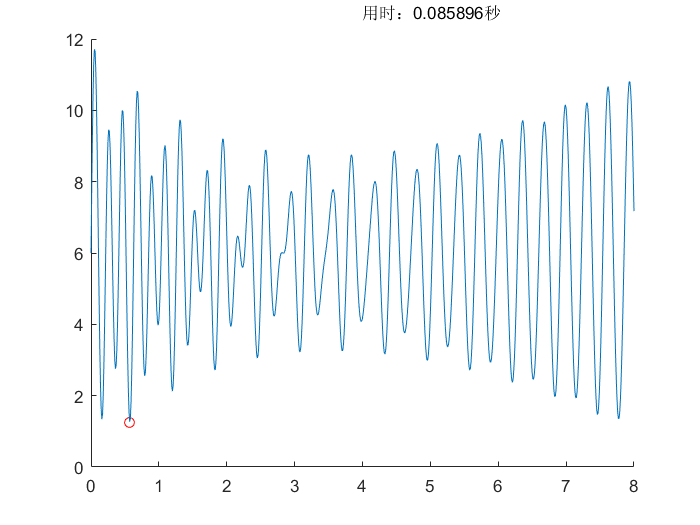
粒子群算法(PSO)
- 优点：
- 搜索能力最快
- 从群体出发，具有并行性
- 可用于求解复杂的非线性优化问题
- 缺点：
- 受到参数影响较大
- 存在早熟收敛问题
- 对初始粒子群的数量有很高的要求
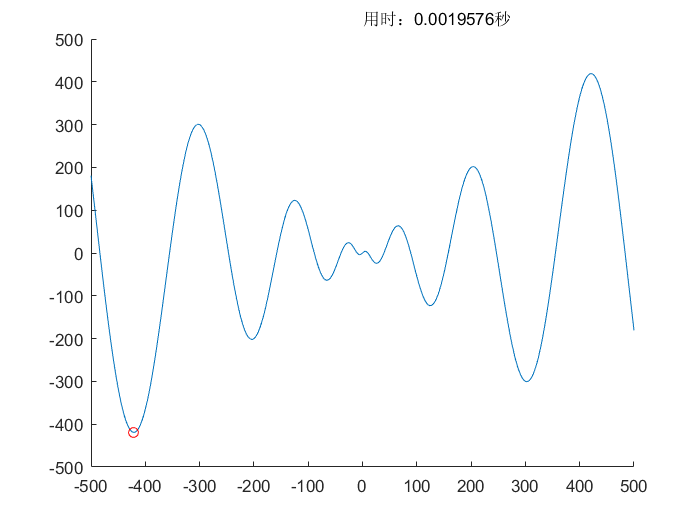
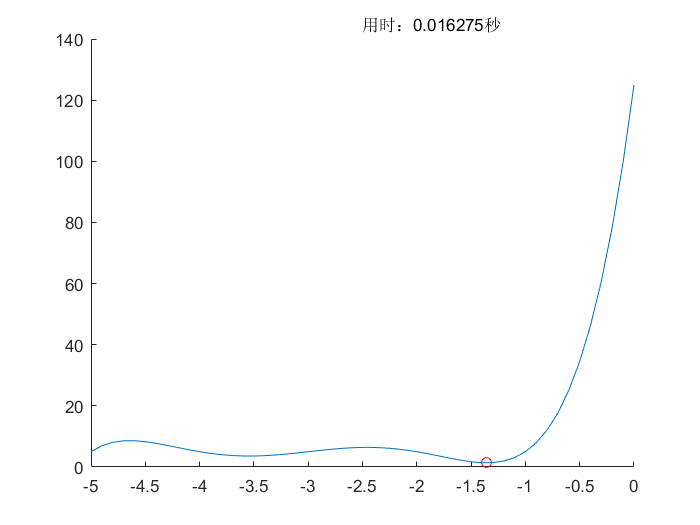
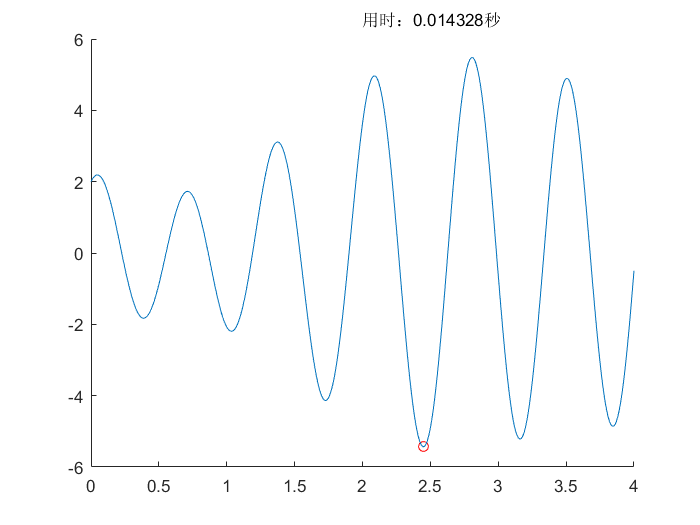
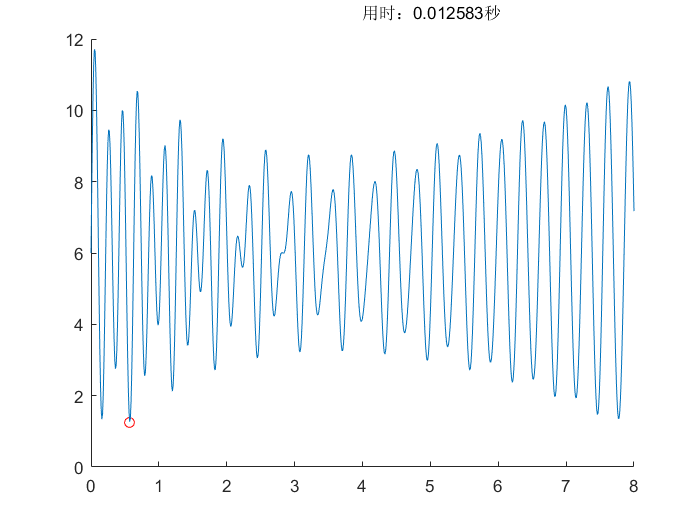
单纯形法(Nelder-Mead)
- 优点：
- 受到参数影响较小
- 具有快速随机的搜索能力
- 可用于求解复杂的非线性优化问题
- 每次迭代都更接近最优解，精度最高
- 缺点：
- 算法性能与初始值有关
- 不适用于多维的最优值求解
- 可能落入其他的局部最小值
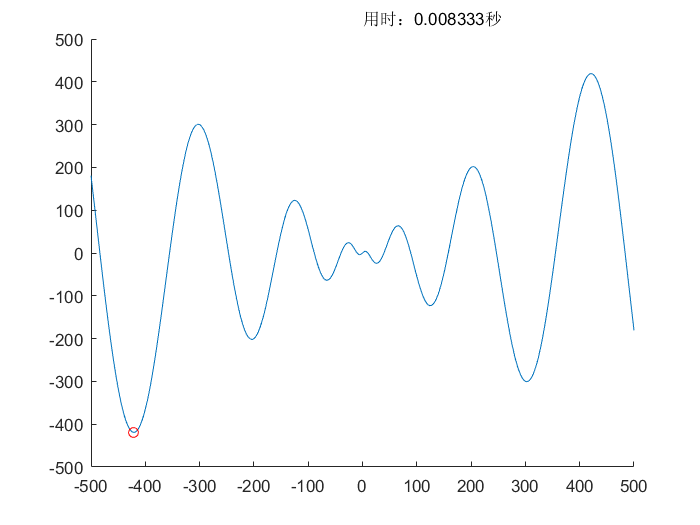
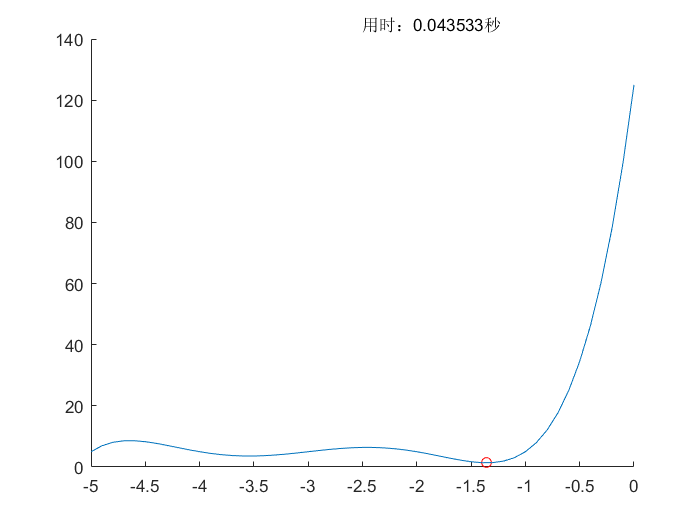
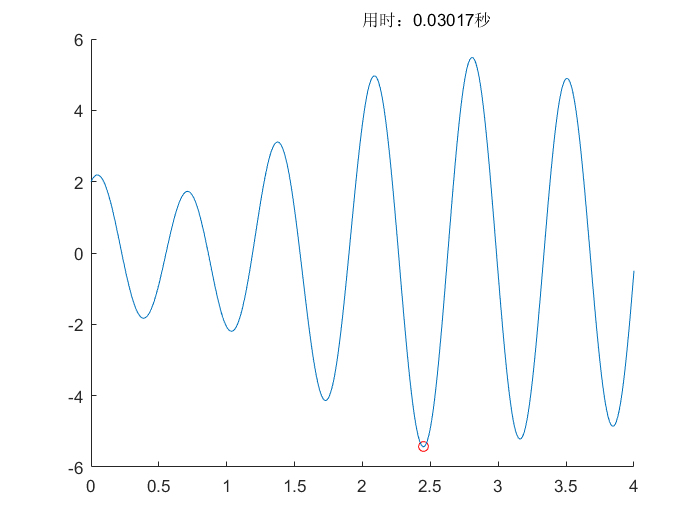
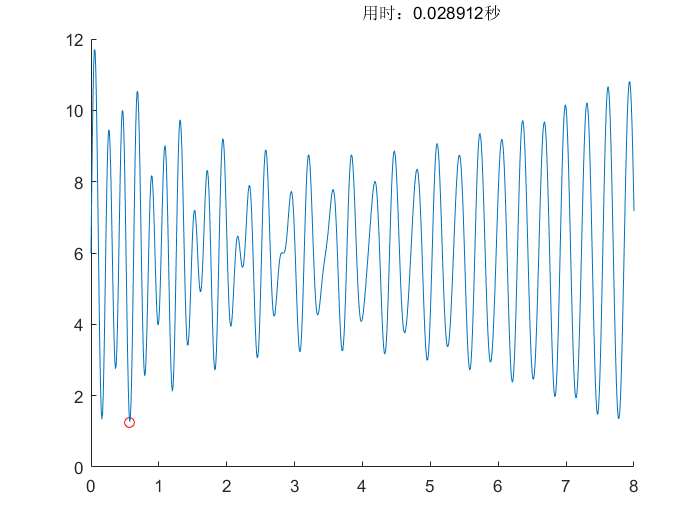
遗传差分算法(DE)
- 优点：
- 受到参数影响较小
- 不会产生早熟收敛问题
- 适用于多维的最优值求解
- 从群体出发，具有并行性
- 算法不依赖初始种群的选择
- 可用于求解复杂的非线性优化问题
- 使用概率机制进行迭代，具有随机性
- 具有可扩展性，容易与其他算法结合
- 缺点：
- 对问题编码表示较为困难
- 因为有大量的比较和选择，可能速度稍慢于遗传算法
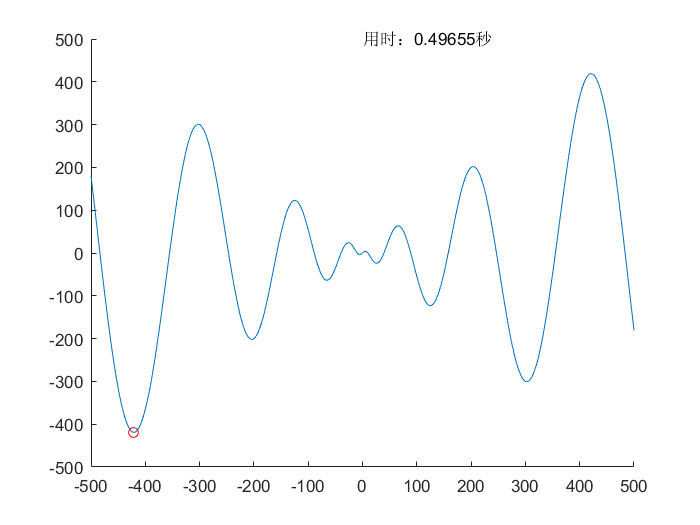
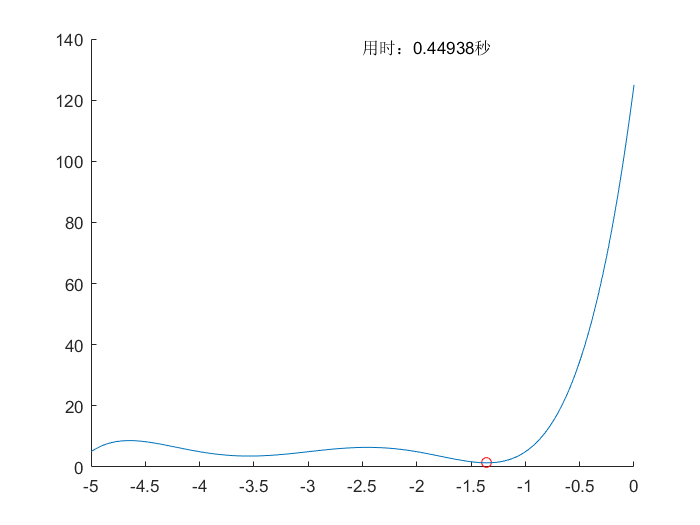
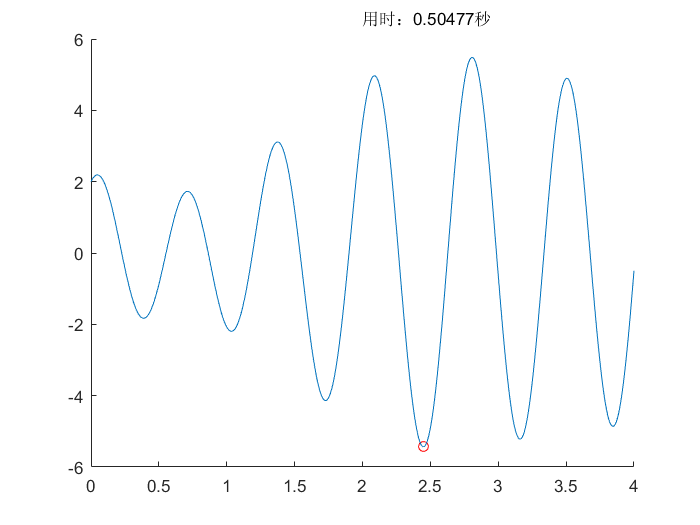
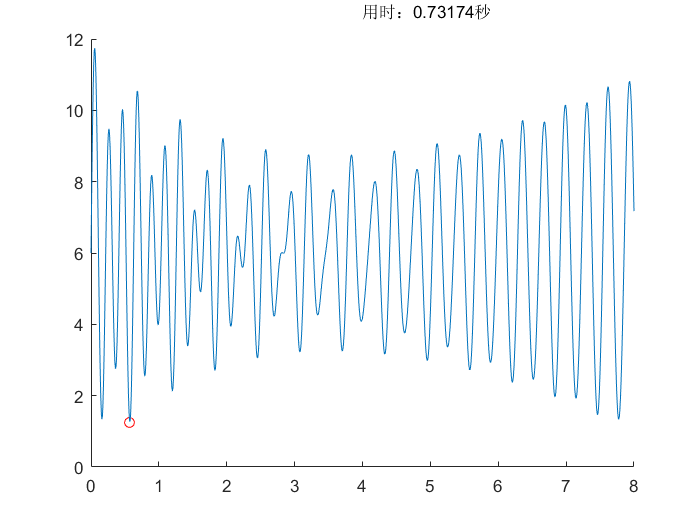
算法对比
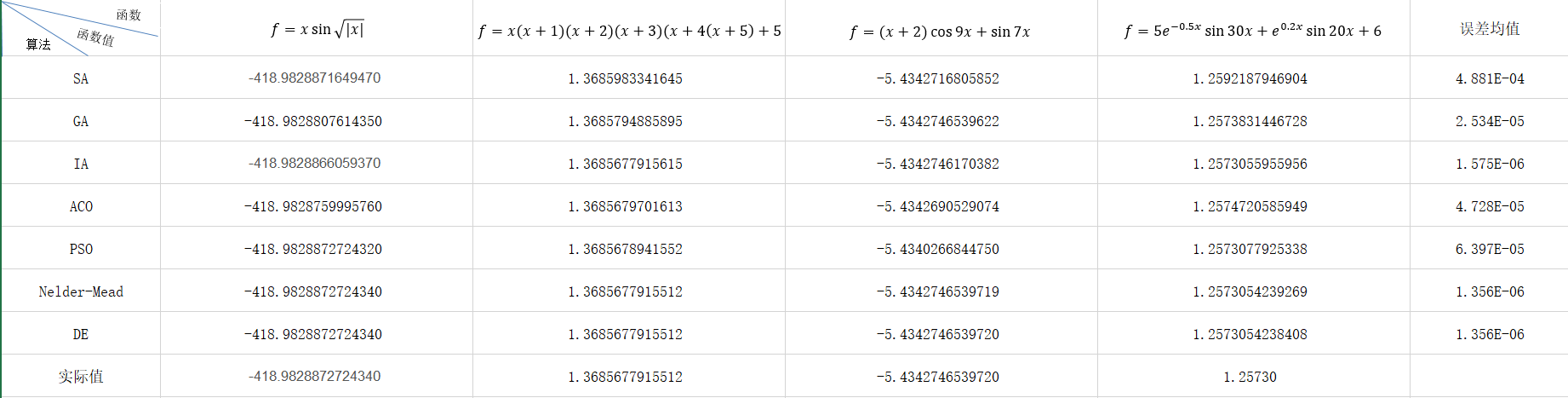搜索精度分析
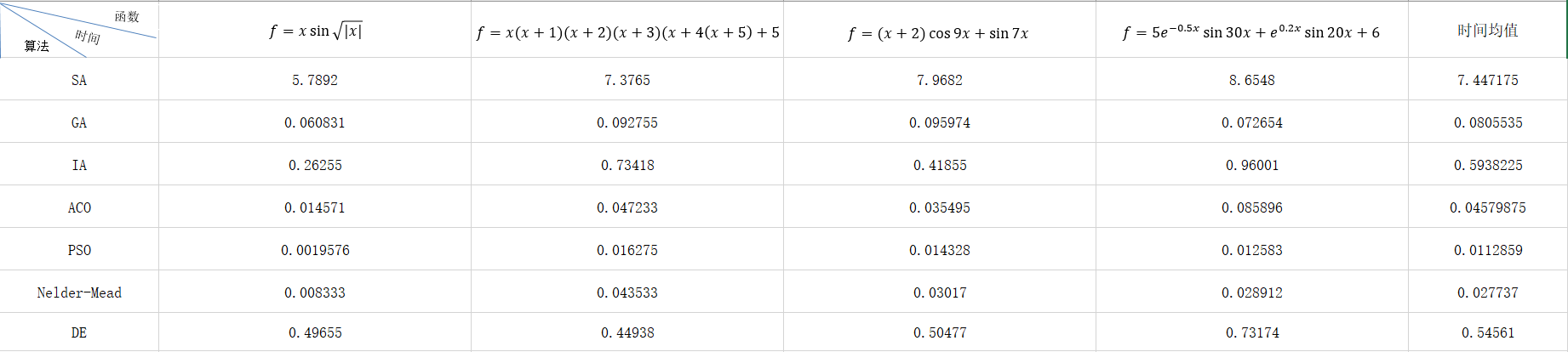所用时间分析特点小结
模拟退火算法(SA)
- 不同问题对温度要求不同，起始温度和温度变化率都会影响搜索精度和时间
- 每次都随机产生一个解，有时很难跳出较深较远的局部最优
- 可以重复运算多次，取多次的最小值，这样可以保证得到全局最优
遗传算法(GA)
- 不同的问题需要的种群个数不同，种群个数越多，搜索精度越高，用时越长
- 迭代次数越高，自然选择越强，保留的结果越好，搜索精度越高，用时越长
- 问题的表示影响遗传算法的效率，用二进制基因串表示还是用十进制表示需要考虑
- 自然选择的方式很重要，采用精英选择或轮盘赌会产生不同的效果
- 遗传算子对算法的影响很大，采用何种交叉方式和多大的变异率最合适
免疫算法(IA)
- 免疫算法包含遗传算法的所有特点
- 免疫过程从记忆细胞中取出部分，提高搜索效率
- 免疫过程随机产生另一部分抗体，给搜索到其他更优点创造了可能性
- 每次的免疫过程都相当于一次遗传算法，因此免疫次数越多，精度越高，时间越长
蚁群算法(ACO)
- 和自然界中蚁群一样，蚂蚁越多，搜索精度越高，但是计算量大，用时更长
- 迭代次数越高，信息素的作用时间越长，所求结果更好，精度更高，用时更长
粒子群算法(PSO)
- 和自然界中飞鸟一样，飞鸟越多越容易遇到全局最优解，搜索精度越高，用时更长
- 迭代次数越高，飞鸟之间的信息交换越多，所求结果更好，精度更高，用时更长
- 粒子群算法可以实现高度的并行计算，因此在搜索函数最值方面速度最快
单纯形法(Nelder-Mead)
- 单纯形法是一种收缩算法，如果初始点选择在局部极小值区域，会收缩到局部最小
- 和SA相同，可以重复运算多次，取多次的最小值，这样可以保证得到全局最优。
- 和其他算法不同，没有随机性，每次迭代都产生比上一次更优的解，搜索精度最高
差分进化算法(DE)
- 差分进化算法类似于改进版的遗传算法，更加适合于多维最优值求解
- 和遗传算法不同的是具有差分性质，能够更容易地跳出当前的局部解
- 淘汰机制也十分简单，将子代和父代对比，直接淘汰表现差的解，精英选择