差分进化算法

背景介绍

DE(Differential Evolution Algorithm):是一种高效的全局优化算法。它也是基于群体的启发式搜索算法，群中的每个个体对应一个解向量。差分进化算法的进化流程则与遗传算法非常类似，都包括变异、杂交和选择操作，但这些操作的具体定义与遗传算法有所不同。

核心思想

1. 随机产生一些初始种群

2. 根据适应度对种群采用某种方式进行自然选择

3. 对选择剩余的种群进行差分遗传，产生新的种群

4. 对父代和子代留一处理，回到步骤2，直到满足某个终止条件

5. 此时剩余的是适应度较好的种群，比较可得该算法的最优解

算法流程

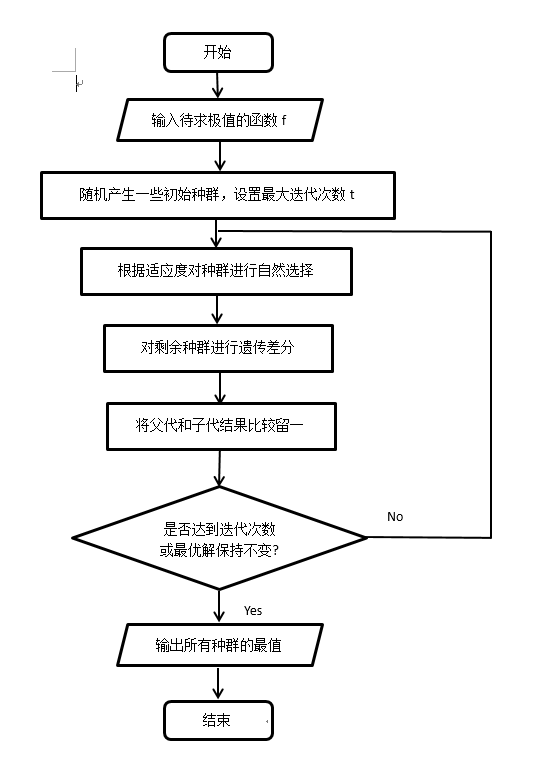
代码实战

代码中所用测试函数可以查看相关文档，测试函数(Test Function)

DE_main.m

clear;clc;close all;
%自变量取值范围
range_x=[ones(1,1),-ones(1,1)]*500;
%维度
n=size(range_x,1);
%种群数量
gn=100;
%迭代次数
times=1000;
%交叉概率
cr=0.5;
%随机产生一些种群
group=zeros(n,gn);
for k=1:n
    group(k,:)=(rand(1,gn))*(range_x(k,2)-range_x(k,1))+range_x(k,1);
end
%设置当前最优解
best_value=zeros(1,times);
tic;
for k=1:times
    for i=1:gn
        %基因重组的过程中可能发生染色体变异
        exchange=randperm(gn,3);
        h=group(:,exchange(1))+rand(1)*(group(:,exchange(2))-group(:,exchange(3)));
        h(h>500)=500;
        h(h<-500)=-500;
        v=group(:,i);
        %染色体交换,保留的物种产生后代时发生基因重组
        for j=1:n
            if cr>rand(1)
                v(j)=h(j);
            end
        end
        if f(v)<f(group(:,i))
            group(:,i)=v;
        end
    end
    best_value(k)=min(f(group));
    if k>100&&abs(best_value(k)-best_value(k-100))<1e-5
        break;
    end
end
time=toc;
disp(['用时：',num2str(time),'秒'])
[mini,index]=min(f(group));
disp(['fmin=',num2str(mini)]);
for k=1:n
    disp(['x',num2str(k),'=',num2str(group(k,index))]);
end
if n==1
    hold on;
    plot(group(index),mini,'ro');
    plot_x=range_x(1):(range_x(2)-range_x(1))/1000:range_x(2);
    plot_y=f(plot_x);
    plot(plot_x,plot_y);
    text((range_x(1)+range_x(2))/2,max(plot_y)+0.1*(max(plot_y)-min(plot_y)),['用时：',num2str(time),'秒']);
    hold off;
end
if n==2
    %所求最小值的函数
    func=@(x1,x2)x1.*sin(sqrt(abs(x1)))+x2.*sin(sqrt(abs(x2)));
    plot_x=range_x(1,1):(range_x(1,2)-range_x(1,1))/1000:range_x(1,2);
    plot_y=range_x(2,1):(range_x(2,2)-range_x(2,1))/1000:range_x(2,2);
    [plot_x,plot_y] =meshgrid(plot_x,plot_y);
    plot_z=func(plot_x,plot_y);
    surf(plot_x,plot_y,plot_z);
    xlabel('x1');
    ylabel('x2');
    zlabel('y');
    hold on;
    plot3(group(1,index),group(2,index),mini,'ko')
    text((range_x(1,1)+range_x(1,2))/2,(range_x(2,1)+range_x(2,2))/2,max(max(plot_z))+0.5*(max(max(plot_z))-min(min(plot_z))),['用时：',num2str(time),'秒']);
    hold off;
end

f.m

function res=f(x)
func=@(x)(x).*sin(sqrt(abs(x)));
res=zeros(1,size(x,2));
for i=1:size(x,1)
    res=res+func(x(i,:));
end

实验结果

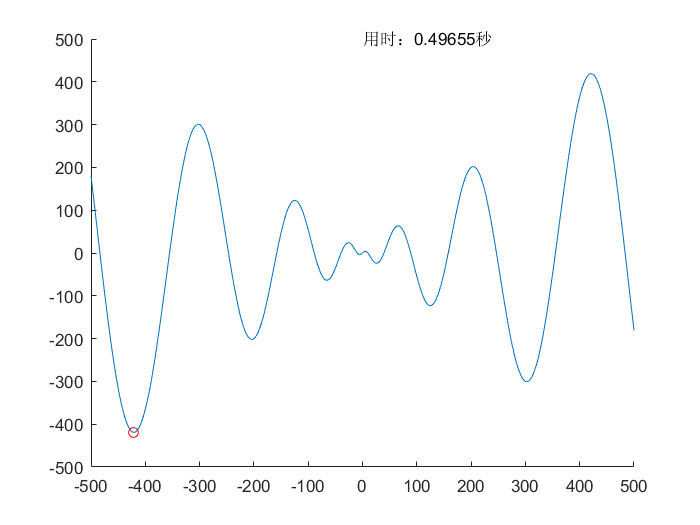
$$f(x)=x \cdot \sin(\sqrt{\lvert x \rvert}) \ , \ x \in [-500,500]$$

$$理论值：f(x)_{min}=f(-420.96874592006)=-418.982887272434$$

$$所求值：f(x)_{min}=f(-420.975929624477)=-418.982887272434$$

性能比较

优点：
- 受到参数影响较小
- 不会产生早熟收敛问题
- 适用于多维的最优值求解
- 从群体出发，具有并行性
- 算法不依赖初始种群的选择
- 可用于求解复杂的非线性优化问题
- 使用概率机制进行迭代，具有随机性
- 具有可扩展性，容易与其他算法结合

缺点：

对问题编码表示较为困难
因为有大量的比较和选择，可能速度稍慢于遗传算法