Fisher线性判别

原理解读

  Fisher线性判别:由Fisher于1936年提出，是一种经典的线性学习方法，其根据方差分析的思想建立起来的一种线性判别法，该判别方法对总体的分布不做任何要求。

核心思想

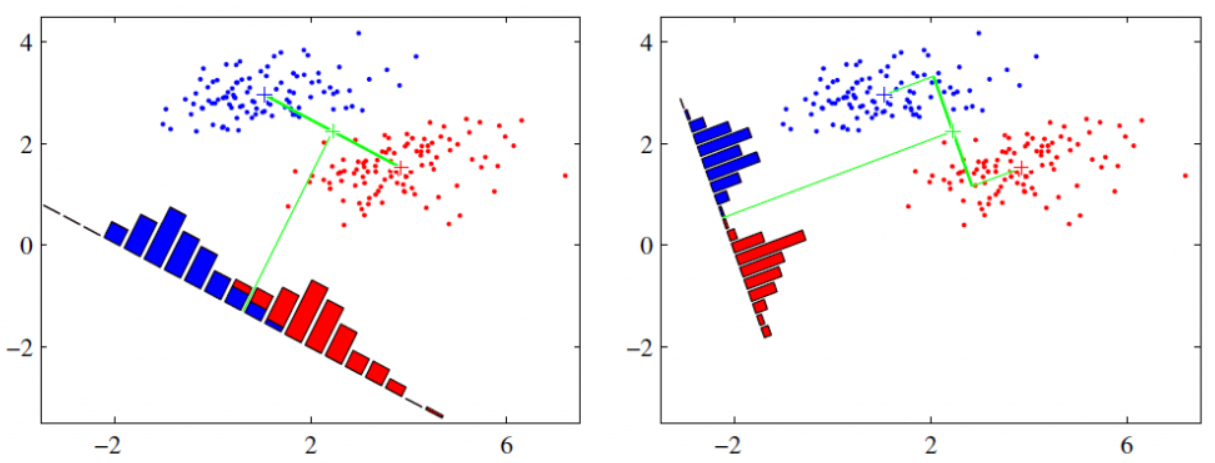
核心思想非常朴素，用周志华老师的话就是：给定训练样例集，设法将样例投影到一条直线上，使得同类样例的投影点尽可能接近，异类样例的投影点尽可能远离。在对新样本进行分类时，将其投影到同样的这条直线上，根据投影点的位置来确定新样本的类别。

设$\mu_i, \Sigma_i, i \in {0, 1}$分别表示第i类样本的均值向量和协方差矩阵。
设投影直线的表达式为$y = \omega x$，则将样本点投影到直线上，两类样本的投影中心分别为$\omega^T \mu_0, \omega^T \mu_0$，两类样本的协方差分别为$\omega^T \Sigma_0 \omega, \omega^T \Sigma_1 \omega$

为了寻找一个最优的投影直线，因此我们要尽量使得类内距离越小越好，类间距离越大越好。可以认为是一种高内聚，低耦合的思想。

要使同类样例投影点的协方差尽可能小，即$\omega^T \Sigma_0 \omega + \omega^T \Sigma_1 \omega$尽可能小，要使不同样例投影中心的距离尽可能大，即$||\omega^T \mu_0 - \omega^T \mu_1||_2^2$尽可能大。

因此得到了我们的目标函数
$$ \begin{align} J & = \frac{||\omega^T \mu_0 - \omega^T \mu_1||_2^2}{\omega^T \Sigma_0 \omega + \omega^T \Sigma_1 \omega} \ & = \frac{\omega^T (\mu_0 - \mu_1)(\mu_0 - \mu_1)^T \omega}{\omega^T (\Sigma_0 + \Sigma_1) \omega} \end{align}$$

我们定义类内散度矩阵
$$ S_{\omega} = \Sigma_0 + \Sigma_1 = \sum_{x \in X_0}(x - \mu_0)(x - \mu_0)^T + \sum_{x \in X_1}(x - \mu_1)(x - \mu_1)^T $$

我们定义类间散度矩阵
$$ S_b = (\mu_0 - \mu_1)(\mu_0 - \mu_1)^T $$

则目标函数可以重写为
$$ J = \frac{\omega^T S_b \omega}{\omega^T S_{\omega} \omega}$$

求解过程

因为分子和分母都是关于$\omega$的二次项，因此解与$\omega$的长度无关，仅仅与其方向有关，也就是说，若$\omega$是这个问题的一个解，那么对于任意常数$\alpha$，有$\alpha \omega$也是这个问题的解。因此令$\omega^T S_{\omega} \omega = 1$，则目标函数等价于
$$\underset{\omega}{argmin} \ -\omega^T S_b \omega, \ s.t. \ \omega^T S_{\omega} \omega = 1$$

使用拉格朗日乘子法可求得
$$S_b \omega = \lambda S_{\omega} \omega$$
因为$S_b \omega = (\mu_0 - \mu_1)(\mu_0 - \mu_1)^T \omega, \ (\mu_0 - \mu_1)^T \omega$是标量，因此可以设
$$S_b \omega = \lambda (\mu_0 - \mu_1)$$

综合上面两个式子可以得到
$$\omega = S_{\omega}^{-1}(\mu_0 - \mu_1)$$

代码实战

FISHER_train.m

clear;clc;close all;
% x为样本，行数代表特征数，列数代表样本数,以列向量的形式输出，label为样本所对应的类别
train_x=[0.5,0.5,0.8,0.2,0.1;...
    0.8,0.7,0.6,0.2,0.4];
% 1为第一类，0为第二类
train_y=[1,1,1,0,0];
%样本数
train_num=size(train_x,2);
%特征数
feat_num=size(train_x,1);
x1=mean(train_x(:,train_y==1),2);
x2=mean(train_x(:,train_y==0),2);
sw=(train_x(:,train_y==1)-repmat(x1,1,sum(train_y==1)))*(train_x(:,train_y==1)-repmat(x1,1,sum(train_y==1)))'...
    +(train_x(:,train_y==0)-repmat(x2,1,sum(train_y==0)))*(train_x(:,train_y==0)-repmat(x2,1,sum(train_y==0)))';
%求出权向量
w=(sw\(x1-x2))';
fprintf('权向量为:');
disp(w);
fprintf('\n\n');
disp('运行FISHER_test开始测试');

FISHER_test.m

close all;
%输入测试集
test_x=rand(2,10);
%测试集样本数
test_num=size(test_x,2);
b_test=w*test_x;
%找到分割平面
tem=w*train_x;
if min(tem(train_y==1))>max(tem(train_y==0))
    mid=(min(tem(train_y==1))+max(tem(train_y==0)))/2;
    test_y=b_test>mid;
else
    mid=(max(tem(train_y==1))+min(tem(train_y==0)))/2;
    test_y=b_test<mid;
end
%如果是二维特征，可以用平面坐标系绘图表示
if feat_num==2
    hold on;
    axis equal;
    k1=w(2)/w(1);
    if w(1)==0
        line1_x=[1,1];
        line1_y=[-1,1];
        x_mid=[-1,1];
        y_mid=[mid,mid];
    elseif w(2)==0
        line1_x=[-1,1];
        line1_y=[1,1];
        x_mid=[mid,mid];
        y_mid=[-1,1];
    else
        line1_x=[-1,1];
        line1_y=k1*line1_x+1;
        x_mid=[-1,1];
        y_mid=(mid-w(1)*x_mid)/w(2);
    end
    %画出投影到一维直线的形状
    plot(line1_x,line1_y,'k');
    plot(x_mid,y_mid,'k');
    
    b_train=w*train_x;
    point_train=zeros(2,train_num);
    %画出训练集投影直线
    for i=1:train_num
        if train_y(i)==1
            point_train(:,i)=[w(1),w(2);k1,-1]\[b_train(i);-1];
            plot([train_x(1,i),point_train(1,i)],[train_x(2,i),point_train(2,i)]','r');
            plot(train_x(1,i),train_x(2,i),'r*');
        else
            point_train(:,i)=[w(1),w(2);k1,-1]\[b_train(i);-1];
            plot([train_x(1,i),point_train(1,i)],[train_x(2,i),point_train(2,i)]','g');
            plot(train_x(1,i),train_x(2,i),'g*')
        end
    end
    point_test=zeros(2,test_num);
%     画出测试集投影直线
    for i=1:test_num
        if test_y(i)==1
            point_test(:,i)=[w(1),w(2);k1,-1]\[b_test(i);-1];
            plot([test_x(1,i),point_test(1,i)],[test_x(2,i),point_test(2,i)]','r');
            plot(test_x(1,i),test_x(2,i),'ro');
        else
            point_test(:,i)=[w(1),w(2);k1,-1]\[b_test(i);-1];
            plot([test_x(1,i),point_test(1,i)],[test_x(2,i),point_test(2,i)]','g');
            plot(test_x(1,i),test_x(2,i),'go')
        end
    end
else
    disp('The Feature Is Not Two-Dimensional');
end

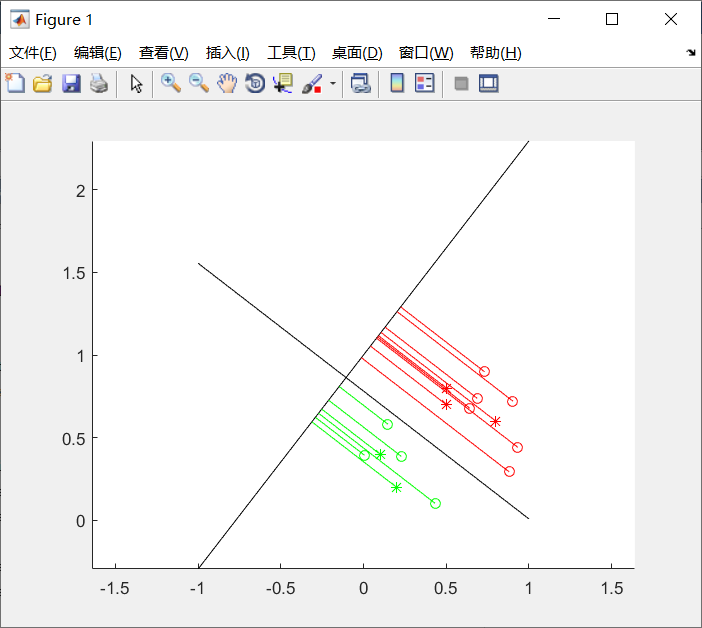
实验结果

Fisher优缺点

• 优点：
  • 无需参数估计，无需训练。
  • 算法简单，易于理解和实现。
  • 计算量小，能够达到实时的效率。
• 缺点：
  • 对于多分类问题，实现起来较为复杂。
  • 样本不平衡时，尤其是一类样本多，其他类样本少时会产生严重的问题。