bayes

原理解读

朴素贝叶斯:基于贝叶斯定理，采用了属性条件独立性假设，对已知类别，假设所有属性相互独立，也就是假设每个属性独立地对分类结果发生影响。发源于古典数学理论，而且所需估计的参数很少，算法也较为简单，但是正是因为其假设属性之间相互独立，因此在实际应用中往往是不成立的，所以给模型的正确性带来了一定的影响。

核心思想

贝叶斯定理

$$P(c|x) = \frac{P(c)P(x|c)}{P(x)}$$
介绍一些非常重要的概念，**$P(c)$称为先验概率，$P(x|c)$是样本x相对于类标记c的类条件概率，$P(x)$是用于归一化的因子，给定样本x，归一化因子$P(x)$与类标记无关。因此估计$P(c|x)$就转化为如何基于训练数据集来估计先验$P(c)$和类条件概率$P(x|c)$**。

极大似然估计

朴素贝叶斯模型的训练过程就是一个参数估计的过程，对于这个问题，机器学习分成了两派，频率派和贝叶斯派。
频率派认为：参数虽然未知，但是却存在着固定值，可以通过优化似然函数等准则确定参数值。
贝叶斯派认为：参数是未观察到的随机变量，其本身也有分布，因此可以假设参数服从一个先验分布，然后基于观测到的数据计算参数的后验分布。

极大似然估计(MLE, Maximum Likelihood Estimation)是根据数据采样来估计概率分布的经典方法。令$D_c$表示训练集D中第c类样本组成的集合，假设这些样本是独立同分布的，则参数$\theta_c$对于数据集$D_c$的似然是
$$P(D_c|\theta_c) = \prod_{x \in D_c} P(x|\theta_c)$$
对$\theta_c$进行极大似然估计，就是去寻找能最大化似然$P(D_c|\theta_c)$的参数值$\hat{\theta}_c$。通常为了计算方便，使用对数似然。
$$\begin{align} LL(\theta_c) & = log(P(D_c|\theta_c)) \ & = \sum_{x \in D_c} log(P(x|\theta_c)) \end{align}$$
此时参数$\theta_c$的极大似然估计$\hat{\theta}_c$为
$$\hat{\theta}_c = \underset{\theta_c}{argmax} \ LL(\theta_c)$$

在连续属性情形下，假设概率密度函数$p(x|c) ~ N(\mu_c, \sigma_c^2)$，则参数$\mu_c$和$\sigma_c^2$的极大似然估计为
$$\hat{\mu}c = \frac{1}{|D_c|}\sum{x \in D_c}x$$
$$\hat{\sigma}c^2 = \frac{1}{|D_c|}\sum{x \in D_c}(x - \hat{\mu}_c)(x - \hat{\mu}_c)^T$$

朴素贝叶斯分类器

基于条件独立性假设，因此贝叶斯定理可以重写为
$$\begin{align} P(c|x) & = \frac{P(c)P(x|c)}{P(x)} \ & = \frac{P(c)}{P(x)}\prod_{i = 1}^{d}P(x_i|c) \end{align}$$
因为对所有类别来说，$P(x)$相同，可以看出朴素贝叶斯分类器的训练过程就是基于训练集D来估计先验概率$P(c)$和类条件概率$P(x_i|c)$。

令$D_c$表示训练集D中第c类样本组成的集合，则先验概率为
$$P(c) = \frac{|D_c|}{D}$$
令$D_{c, x_i}$表示$D_c$中第i个属性取值为$x_i$的样本组成的集合，则离散属性类条件概率为
$$P(x_i|c) = \frac{|D_{c, x_i}|}{|D_c|}$$
对于连续属性的类条件概率求解时，假定$P(x_i|c) ~ N(\mu_{c, i}, \sigma_{c, i}^2)$，则连续属性类条件概率为
$$P(x_i|c) = \frac{1}{\sqrt{2 \pi}\sigma_{c, i}}exp(-\frac{(x - \mu_{c, i})^2}{2 \sigma_{c, i}^2})$$

计算好上面这两个参数后，直接代入公式
$$\hat{c} = \underset{c \in \gamma}{argmax} \ P(c) \prod_{i = 1}^{d}P(x_i|c)$$
其中$\gamma$为所有类别数，对每一个类别都进行计算，哪一个类别得到的值最大，则将样本分到哪一个类别中去即可。

代码实战

BAYES_train.m

clear;clc;
%x为样本，行数代表特征数，列数代表样本数,以列向量的形式输出
train_x=[0.8,0.9,0.1,0.2,0.1,0.2;...
    0.8,0.9,0.9,0.2,0.1,0.8];
%1为第一类，2为第二类，3为第三类
train_y=[1,1,3,2,2,3];
%特征数
feat_num=size(train_x,1);
%样本数
train_num=size(train_x,2);
tem=tabulate(train_y);
%p_y为先验概率
p_y=tem(:,3)/100;
u_sigma=zeros(feat_num,2,length(p_y));
for i=1:length(p_y)
   for j=1:feat_num
       %u_sigma(j,:,i)代表第i类，第j个特征的均值和方差
       u_sigma(j,:,i)=[mean(train_x(j,train_y==i)),std(train_x(j,train_y==i))];
   end
end

BAYES_test.m

close all;
%输入测试集
test_x=rand(2,100);
%测试集样本数
test_num=size(test_x,2);
%temp保存类条件概率
temp=zeros(feat_num,size(u_sigma,3));
test_y=zeros(1,test_num);
for i=1:test_num
    for j=1:feat_num
        for k=1:size(u_sigma,3)
            %第j行第k列代表第i个样本第k类第j个特征的概率，即类条件概率P(x_j|y=k)
            temp(j,k)=normpdf(test_x(j,i),u_sigma(j,1,k),u_sigma(j,2,k));
        end
    end
    %根据条件独立性假设，将类条件概率相乘得到后验概率
    p=prod(temp);
    %求出最大后验概率的类别
    [~,test_y(i)]=max(p);
end
if feat_num==2
    hold on;
    color_bar=rand(size(u_sigma,3),3);
    for i=1:train_num
        plot(train_x(1,i),train_x(2,i),'color',color_bar(train_y(i),:),'marker','*');
    end
    for i=1:test_num
        plot(test_x(1,i),test_x(2,i),'color',color_bar(test_y(i),:),'marker','o');
    end
    hold off;
    %如果不是两个特征不能用平面坐标系表示
else
    disp('The Feature Is Not Two-Dimensional');
end

实验结果

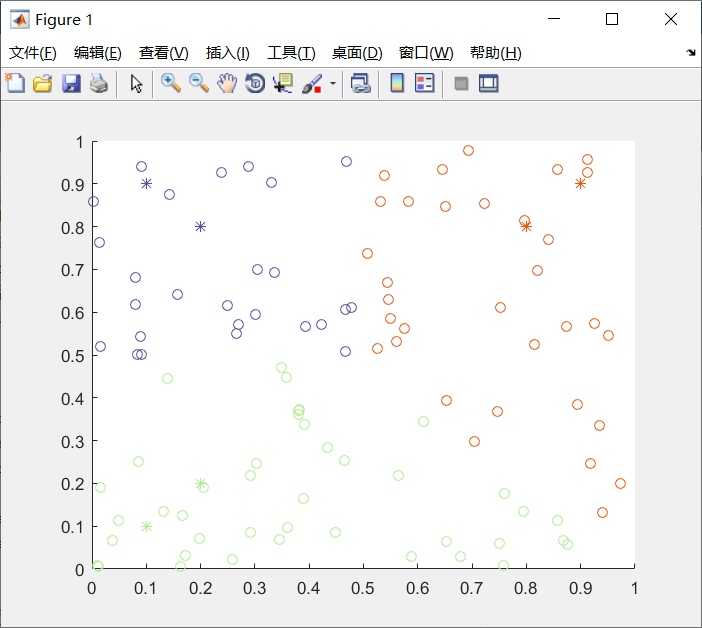
bayes

朴素贝叶斯优缺点

优点：
- 算法简单，易于理解和实现，且模型无需训练。
- 计算量小，能够达到实时的效率。
- 同样适合于对于多分类问题。

缺点：

因为假设各属性独立，因此实际生活中可能出现问题。
样本不平衡时，尤其是一类样本多，其他类样本少时会产生严重的问题。