动态规划(Dynamic Programming)

发表于 | 分类于 ， | | 本文总阅读数 次
| 字数统计: 2.5k | 阅读时长 ≈ 11
Dynamic Programming

动态规划

原理介绍

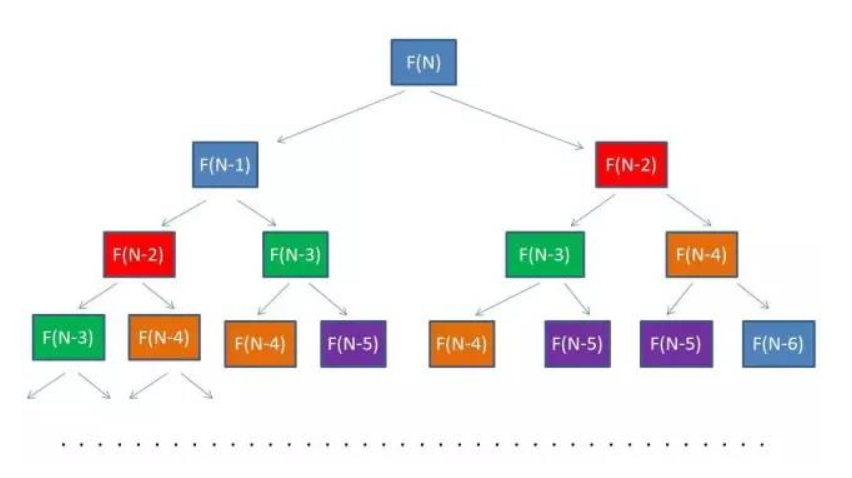
   Dynamic Programming(DP):动态规划，是运筹学的一个分支，是求解决策过程最优化的数学方法。于1957年被Richard Bellman(理查德·贝尔曼)提出。其中的Programming不是编程的意思，而是指一种表格处理法，把每一步得到的子问题的结果存储在表格里，每次遇到子问题时不需要再求解一遍。其本质也是一种分治算法，其不同点在于分治算法将原问题分解为若干子问题，自顶向下求解各子问题，再合并子问题的解。动态规划也是把原问题分解为若干子问题，然后自底向上，先求解最小的子问题，把结果存储起来，求解大问题时直接查询小问题的解，避免了大量的重复计算，提高了算法效率。其本质为：递归+记忆化

dynamic

问题条件

最优子结构

  最优子结构性质是指问题的最优解包含其子问题的最优解。最优子结构是使用动态规划的最基本条件，如果问题不具有最优子结构性质，就不可以使用动态规划解决。

子问题重叠

  子问题重叠是指再求解子问题的过程中，有大量的子问题是重复的，那么只需要求解依次，然后存储在表格中，以便使用时查询。这不是动态规划的必要条件，但是可以充分体现动态规划的优势。

算法步骤

  (1)分析最优解的结构特征
  (2)定义状态转移方程(递归式)
  (3)自底向上计算最优解并记录

经典例题(0-1背包)

问题描述

  假设山洞里有n个宝物，每种宝物有一定重量w和相应的价值v，背包的装载能力有限，只能运走重量为m的宝物，宝物不可以分割，如何使背包运走物品的价值最大？
  第一行先输入宝物的数量n，和背包的承载重量m，然后每一行输出一个宝物对应的重量w和价值v(用空格分开)

1
2
3
4
5
6
5 10 # 宝物数n和背包能装载的重量m
2 6 #每个宝物的重量w和价值v
5 3
4 5
2 4
3 6

算法分析

  和普通背包问题不同，如果盲目的装入当前单位重量价值最高的物品，可能导致背包剩余空间较大，达不到最优解。首先分析问题的结构特征，如果第i个宝物装入背包是问题的最优解，背包总重量$m-w_i$一定是问题$\lbrace a_1, a_2, \ldots, a_n \rbrace$的最优解。因此该问题具有最优子结构性质。
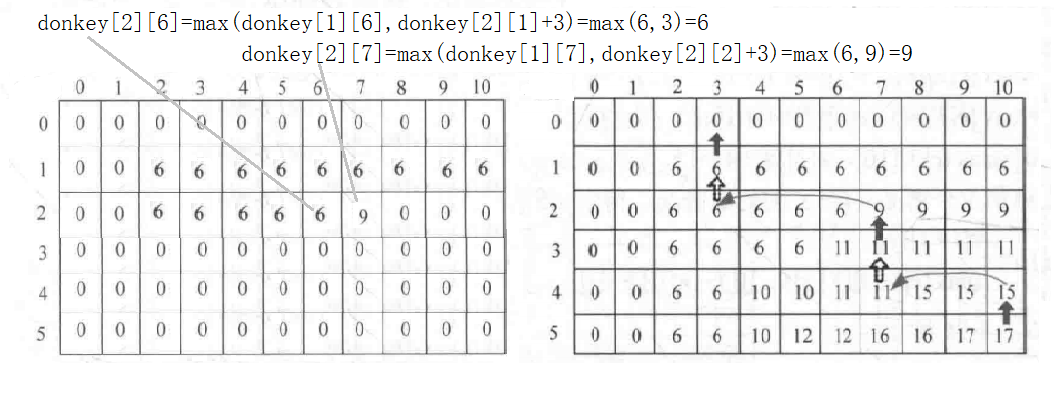
  根据分析可知，判断第i个宝物装入重量为j的背包时会转化为两种可能，装入或者不装入，不放入时，问题变为前i-1个宝物装入重量为j的背包的最大价值。放入时，问题变为前i-1个宝物装入重量为j-wi的背包的最大价值加上第i个宝物的价值vi。即比较两者的最大值，用donkey[i][j]表示第i个宝物装入容量为j的背包里的最大价值。
$donkey[i][j] = \begin{cases} donkey[i-1][j], & j<w_i \ \max{donkey[i-1][j], donkey[i-1][j-w[i]]+v[i]}, & j \ge w_i \end{cases}$

0-1背包图解

1

python代码实战

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import sys

print('请输入宝物数量和驴子承载重量:')
for line in sys.stdin:
    count, weight = line.strip().split()
    count, weight, treasure, donkey, i, j, plan = int(count), int(weight), [], [[0 for i in range(int(weight) + 1)] for j in range(int(count) + 1)], 0, 0, []
    print('请输入每个宝物的重量和价值')
    for i in range(count):
        treasure.append([int(x) for x in sys.stdin.readline().strip().split()])
    for i in range(1, count + 1):
        for j in range(1, weight + 1):
                donkey[i][j] = max(donkey[i - 1][j - treasure[i - 1][0]] + treasure[i - 1][1], donkey[i - 1][j]) if j >= treasure[i - 1][0] else donkey[i - 1][j]
    while donkey[i][j] != 0:
        plan, i, j = [['放入第' + str(i) + '个宝物'] + ['\n'] + plan, i - 1, j - treasure[i - 1][0]] if donkey[i][j] != donkey[i - 1][j] else [plan, i - 1, j]
    print('无法放入任何一个宝物') if donkey[-1][-1] == 0 else print(''.join(plan) + '装入宝物的最大价值为:', donkey[-1][-1])

代码运行结果

6

经典例题(最长公共序列)

问题描述

  给定两个序列，如何找出最长公共子序列
  第一行输入字符串s1，第二行输入字符串s2

1
2
ABCADAB # 字符串s1
BACDBA # 字符串s2

算法分析

  首先分析问题是否具有最优子结构的性质，假设$Z_k={z_1,z_2,z_3,\ldots,z_k}$是$X_m={x_1,x_2,x_3,\ldots,x_m}$和$Y_n={y_1,y_2,y_3,\ldots,y_n}$的最长公共组序列，可以有三种情况讨论：
  (1)当$z_k=x_m=y_n$时，则$Z_k={z_1,z_2,z_3,\ldots,z_{k-1}}$是$X_m={x_1,x_2,x_3,\ldots,x_{m-1}}$和$Y_n={y_1,y_2,y_3,\ldots,y_{n-1}}$的最长公共组序列。
  (2)当$z_k \neq x_m,x_m \neq y_n$时，则$Z_k={z_1,z_2,z_3,\ldots,z_k}$是$X_m={x_1,x_2,x_3,\ldots,x_{m-1}}$和$Y_n={y_1,y_2,y_3,\ldots,y_n}$的最长公共组序列。
  (3)当$z_k \neq y_n,x_m \neq y_n$时，则$Z_k={z_1,z_2,z_3,\ldots,z_k}$是$X_m={x_1,x_2,x_3,\ldots,x_m}$和$Y_n={y_1,y_2,y_3,\ldots,y_{n-1}}$的最长公共组序列。
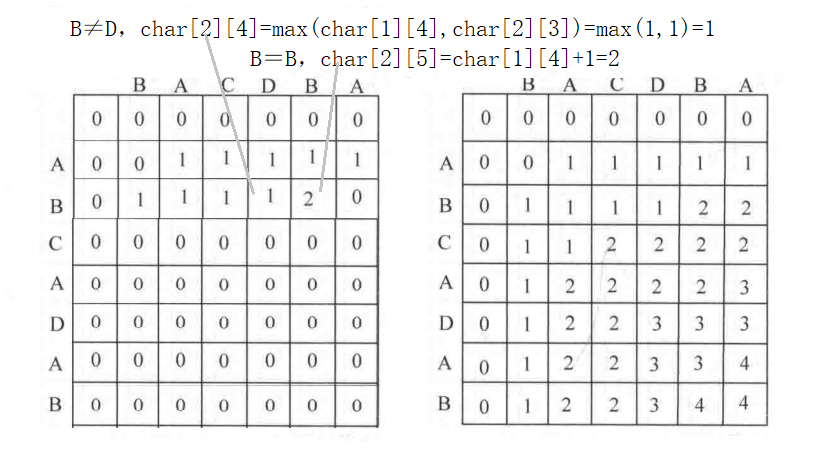
  因此问题满足最优子结构性质，用char[i][j]表示Xi和Yj的最长公共子序列长度。
$char[i][j] = \begin{cases} char[i-1][j-1]+1, & x_i=y_j \ \max{char[i][j-1], char[i-1][j]}, & x_i \neq y_j \end{cases}$

公共子序列图解

2

python代码实战

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import sys

print('输入字符串s1:')
for line in sys.stdin:
    s1 = line.strip()
    print('输入字符串s2:')
    s2 = sys.stdin.readline().strip()
    s1_length, s2_length, i, j, route = len(s1), len(s2), 0, 0, ''
    compare_array, route_array = [[0 for m in range(s2_length + 1)] for n in range(s1_length + 1)], [[0 for m in range(s2_length + 1)] for n in range(s1_length + 1)]
    for i in range(1, s1_length + 1):
        for j in range(1, s2_length + 1):
            compare_array[i][j], route_array[i][j] = [compare_array[i - 1][j - 1] + 1, 1] if s1[i - 1] == s2[j - 1] else([compare_array[i][j - 1], 2] if compare_array[i][j - 1] >= compare_array[i - 1][j] else [compare_array[i - 1][j], 3])
    while i > 0 and j > 0:
        route, i, j = [route + s1[i - 1], i - 1, j - 1] if route_array[i][j] == 1 else ([route, i, j - 1] if route_array[i][j] == 2 else [route , i - 1, j])
    print(s1 + '和' + s2 + '无公共序列') if len(route) == 0 else print(s1 + '和' + s2 + '的最长公共序列的长度为:', len(route), '\n' + s1 + '和' + s2 +'的最长公共序列是:' + route[::-1])

代码运行结果

4

经典例题(字符串编辑距离)

问题描述

  给定两个序列，如何使用最少的增加字符，删除字符，替换字符操作，使两个序列相同？
  第一行输入字符串str1，第二行输入字符串str2

1
2
family # 字符串str1
frame # 字符串str2

算法分析

  分析此题是否具有最优子结构性质，假设char[i][j]是$X_i={x_1,x_2,x_3,\ldots,x_i}$和$Y_j={y_1,y_2,y_3,\ldots,y_j}$的编辑距离的最优解，可以有两种情况讨论：
  (1)当两个字符串满足$x_i=y_j$时，则char[i-1][j-1]是$X_m={x_1,x_2,x_3,\ldots,x_i}$和$Y_n={y_1,y_2,y_3,\ldots,y_j}$的编辑距离的最优解。
  (2)当两个字符串满足$x_i \neq y_j$时，则可以删除字符xi或删除字符yj或将字符xi替换为字符yj，即满足下列条件$\max(char[i-1][j],char[i][j-1],char[i-1][j-1])+1$是$X_m={x_1,x_2,x_3,\ldots,x_i}$和$Y_n={y_1,y_2,y_3,\ldots,y_j}$的编辑距离的最优解。
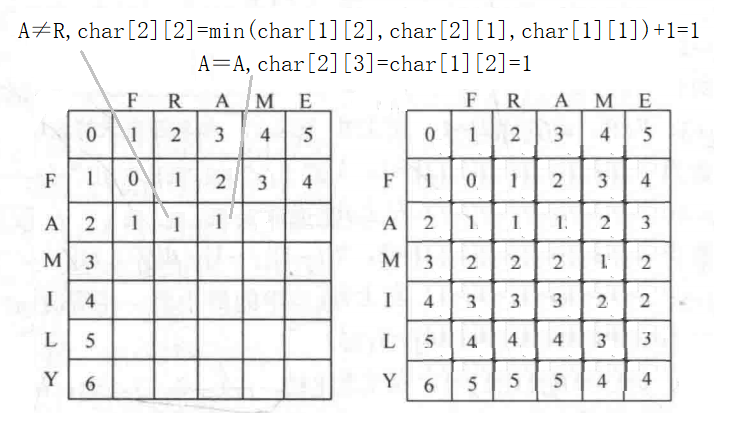
  因此问题满足最优子结构性质，写出其状态转移方程。
$char[i][j] = \begin{cases} char[i-1][j-1], & x_i=y_j \ \max{char[i][j-1], char[i-1][j],char[i-1][j-1]}+1, & x_i \neq y_j \end{cases}$

字符串距离图解

3

python代码实战

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import sys

print('输入字符串str1:')
for line in sys.stdin:
    str1 = line.strip()
    print('输入字符串str2:')
    str2 = sys.stdin.readline().strip()
    str1_length, str2_length, i, j, route = len(str1), len(str2), 0 ,0, []
    compare_array = [list(range(str2_length + 1))] + [[x] + [0] * str2_length for x in range(1,str1_length + 1)]
    for i in range(1, str1_length + 1):
        for j in range(1, str2_length + 1):
            compare_array[i][j] = compare_array[i - 1][j - 1] if str1[i - 1] == str2[j - 1] else min(compare_array[i - 1][j - 1], compare_array[i][j - 1], compare_array[i - 1][j]) + 1
    while i > 0 and j > 0:
        route, i, j = [route, i - 1, j - 1] if str1[i - 1] == str2[j - 1] else ([['将' + str1 + '中' + str(i) + '处的' + str1[i - 1] + '替换为' + str2[j - 1]] + ['\n'] + route, i - 1, j - 1] if compare_array[i - 1][j - 1] + 1 == compare_array[i][j] else([['将' + str1 + '中' + str(i) + '处插入' + str2[j - 1]] + ['\n'] + route, i, j - 1] if compare_array[i][j - 1] + 1 == compare_array[i][j] else [['将' + str1 + '中' + str(i) + '处的' + str1[i - 1] + '删除'] + ['\n'] + route, i - 1, j]))
    print(str1 + '和' + str2 + '的编辑距离是:', compare_array[-1][-1], '\n' + '将' + str1 + '转换为' + str2 + '的操作为:' + '\n' + ''.join(route[:-1]))

代码运行结果

5

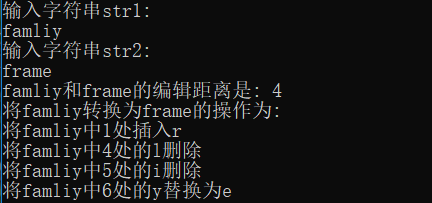
算法总结

  由于动态规划不局限于眼前的最优状态，而是记录了以前的所有状态，因此动态规划具有很强的大局观，可以较为容易地得到全局最优解，因此在实际的生产生活中使用较广。动态规划的关键是分析问题是否具有最优子结构，如果问题具有该性质，说明可以使用动态规划来解决问题。然后是找到其状态转移方程，这也是最难考虑的一个问题。得到了状态转移方程，此问题迎刃而解。

-------------本文结束感谢您的阅读-------------
0%