原理介绍
Depth-First-Search(DFS):深度优先搜索,属于图算法的一种,是一种盲目搜寻法,从初始状态出发,当搜索到某一步时,发现原先选择并不是最优或达不到目标,就退回一步重新选择。根据产生子节点的条件约束,搜索问题的最优解。因此又名回溯法,是一种能进则进,进不了则换,换不了则退的搜索方法。
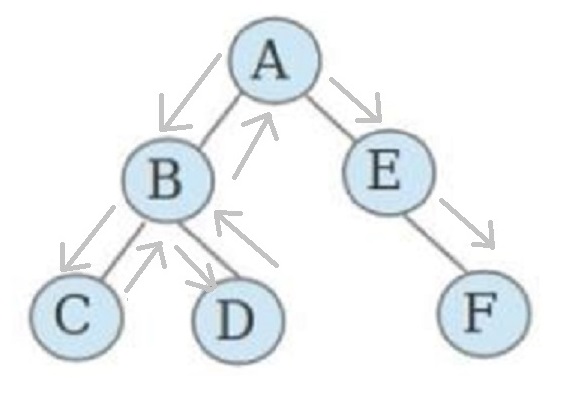
算法条件
解空间
解的组织形式可以规范为一个n元组${x_1,x_2,\ldots,x_n}$,并且对解有取值范围的限定,一般为有穷个,解的个数代表一个结点的分支个数。解空间越小,搜索效率越高,解空间大犹如大海捞针,搜索效率很低。
剪枝函数
剪枝函数又称为隐约束,对能否得到问题的可行解的约束称为约束函数,对能否得到问题的最优解的约束称为限界函数。有了剪枝函数,我们就可以剪掉得不到可行解或最优解的分支,避免了无效搜索,提高搜索的效率。因此剪枝函数的设计是十分重要的。
算法步骤
(1)分析题意,了解题目要求
(2)根据问题分析解空间的形式
(3)根据解空间设计合适的剪枝函数
经典例题(0-1背包)
问题描述
假设山洞里有n个宝物,每种宝物有一定重量w和相应的价值v,背包的装载能力有限,只能运走重量为m的宝物,宝物不可以分割,如何使背包运走物品的价值最大?
第一行先输入宝物的数量n,和背包的承载重量m,然后每一行输出一个宝物对应的重量w和价值v(用空格分开)
1 | 5 10 # 宝物数n和背包能装载的重量m |
算法分析
0-1背包问题和普通背包问题不同的是其解空间为{0,1},即每一个物品都有两种状态,装入或者不装入,因此满足解空间的条件。
分析剪枝函数,如果剩余的价值加上当前的价值都没有已经搜索到的最大价值高,则没有必要继续搜索。
python代码实战
1 | import sys |
代码运行结果
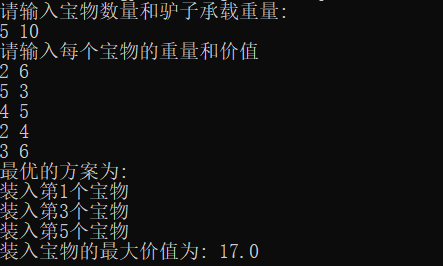
经典例题(n皇后问题)
问题描述
在n×n的国际棋盘上放置彼此不受攻击的n个皇后,按照规则,皇后可以攻击与之在同一行、同一列、统一斜线上的棋子。现在已知又n个皇后,问有多少种不同的放法?
输入皇后的个数n
1 | 4 # 皇后的个数 |
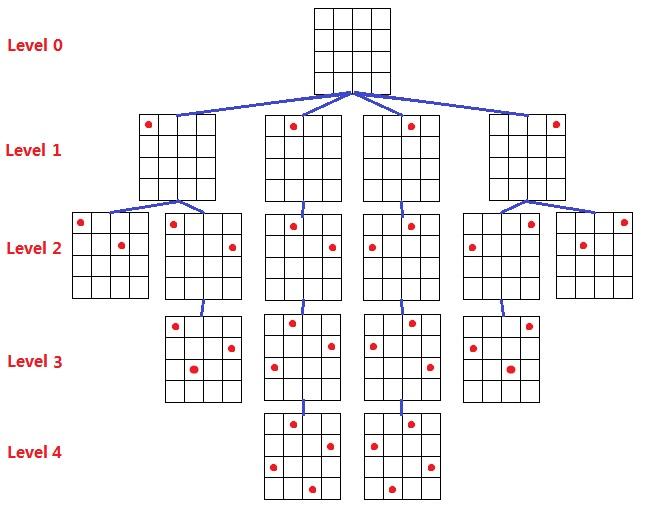
算法分析
n皇后问题不同于0-1背包问题,n皇后的解空间为n,每一个皇后都有n种放法,因此当n很大时,解法的搜索非常缓慢。
分析剪枝函数,已经放置了k个皇后之后,就没有n种不同的放法了,可以通过判断和以前的皇后放法是否冲突来缩小解空间的搜索。
python代码实战
1 | import sys |
代码运行结果
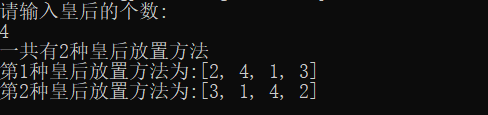
经典例题(旅行商问题TSP)
问题描述
现有n个景点,从第一个景点出发,两个景点之间有数字代表可以直接到达,问如何找到一个路径能够不重复的走遍所有景点回到出发点,而且所经过的路径长度是最短的。
第一行输入景点的个数,第二行输入两地之间可以直接到达的数量,然后每行输入两地和之间的距离
1 | 5 # 景点个数 |
算法分析
旅行商问题(TSP)是一个典型的问题,此问题的解空间为n,每一个景点都可以到与之相连的所有点,因此当景点数很多时,最优解的搜索是十分缓慢的。
分析剪枝函数,剪枝函数容易看出,由于不是任何两个景点都是相连的,而且走过的景点不能再走一次,所以这也大大减少了解空间的个数。
python代码实战
1 | import sys |
代码运行结果
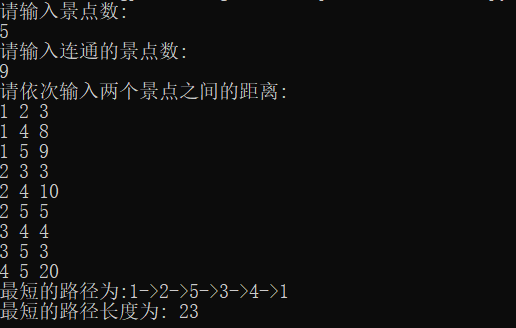
算法总结
深度优先搜索是一个基本搜索方法,对于很多问题来说都可以用深度优先搜索来解决。但不一定是最优的解法,因为深度优先搜索是指数级的时间复杂度,但是对于有些问题不得不使用深度优先进行遍历,因此寻找合适的约束条件可以大大减少时间的开销。