并查集

原理介绍

Union Find:并查集，是一种树型的数据结构，用于处理一些不相交集合的合并及查询问题。在一些有N个元素的集合应用问题中，我们通常是在开始时让每个元素构成一个单元素的集合，然后按一定顺序将属于同一组的元素所在的集合合并。

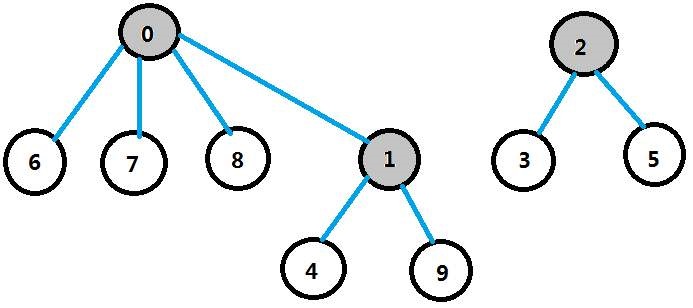
算法步骤

初始化

把每个点所在集合初始化为其自身，通常来说，这个步骤在每次使用该数据结构时只需要执行一次。

查找根结点

查找元素所在的集合，即根节点。为了以后的查找方便，可以在查询时将该结点以及该结点的所有父节点都直接指向根结点，再次查询时即可直接查找到根结点。

合并

将两个元素所在的集合合并为一个集合，合并之前，应先判断两个元素是否属于同一集合，这可用上面的“查找根结点”操作实现，判断两个根结点是否相同来判断是否属于同一集合。

经典例题(岛屿数量)

问题描述

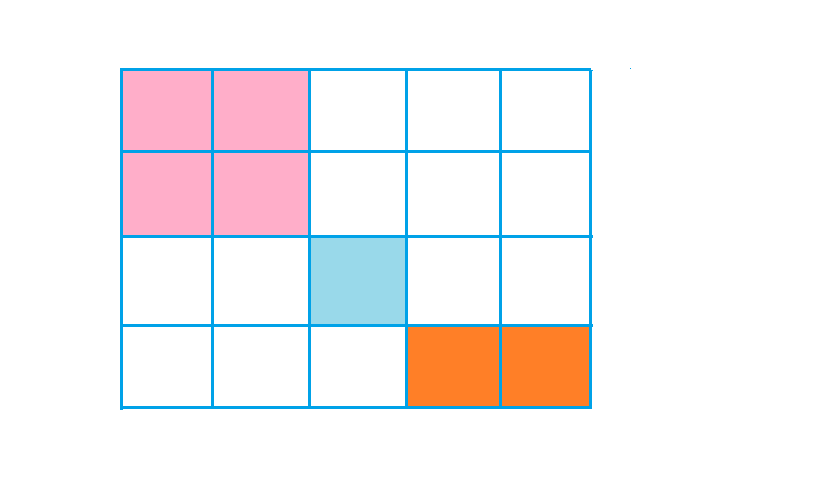
有一个二维的网格地图，其中1代表陆地0代表水，并且该网格的四周全部由水包围。我们对岛屿的定义是四面环水，由相邻的陆地水平或垂直连接形成，现在需要统计岛屿的数量。
输入一行数据，使用空格分隔二维地图的每一行，使用逗号分隔一行中的每一项。

1	1,1,0,0,0 1,1,0,0,0 0,0,1,0,0 0,0,0,1,1 # 输入4×5的地图

算法分析

初始时将每个值为1的点都指向自己(即单独一个点作为一个岛)，count等于值为1的点的个数。然后遍历整个地图，如果该点上下左右有值为1的点则查找两个点的根结点，如果根结点相同说明已经在同一个岛上，否则合并两个岛，count值减1。
将所有点都遍历以后，此时相邻的点都具有同样的根结点，此时的count个数即为岛屿的数量。

python代码实战

import sys

class Union_find:
    def __init__(self, grid):
        row_num, col_num = len(grid), len(grid[0])
        self.count = 0
        self.parent = [-1] * (row_num * col_num)
        for i in range(row_num):
            for j in range(col_num):
                if grid[i][j] == '1':
                    self.parent[i * col_num + j] = i * col_num + j
                    self.count += 1

    def find(self, i):
        root = i
        while self.parent[root] != root: 
            root = self.parent[root]
        while self.parent[i] != root:
            i, self.parent[i] = self.parent[i], root
        return root

    def connection(self, p, q):
        return self.find(p) == self.find(q)

    def union(self, p, q):
        proot = self.find(p)         
        qroot = self.find(q)
        if qroot != proot:
            self.parent[proot] = qroot
            self.count -= 1

print('请输入要查询的地图:')
for line in sys.stdin:
    line = line.strip().split()
    row_num, col_num, grid, direction = len(line), (len(line[0]) + 1) // 2, [], [[1, 0], [0, 1]]
    for tmp in line:
        grid.append(tmp.split(','))
    uf = Union_find(grid)
    for i in range(row_num):
        for j in range(col_num):
            if grid[i][j] == '1':
                for x, y in direction:
                    new_i, new_j = i + x, j + y
                    if new_i < row_num and new_j < col_num and grid[new_i][new_j] == '1':
                        uf.union(i * col_num + j, new_i * col_num + new_j)
    print('该地图中岛屿的数量为:', uf.count)

代码运行结果

算法总结

并查集是一个较为复杂且不太常用的算法，但是可以解决一些特定问题，尤其是解决一些集合关系的问题。该算法可以使具有某些特定关系的点作为一个群体，然后统计整体的群体个数即为整体的类别个数，某个群体中个体的数量即为整体中某一类别的数量。