线性规划

原理介绍

Linear Programming:线性规划，是运筹学中的一个重要分支，研究线性约束条件下线性目标函数的极值问题的数学理论和方法，能从各种限制条件的组合中，选择出最为合理的计算方法，建立线性规划模型，从而求得最佳结果。广泛应用于军事作战、经济分析、经营管理和工程技术等方面。为合理地利用有限的人力、物力、财力等资源作出的最优决策，提供科学的依据。

算法基础

线性规划标准型

对于复杂的线性规划问题，很难采用初中数学的画图法解决，一般要把问题转化为线性规划标准型。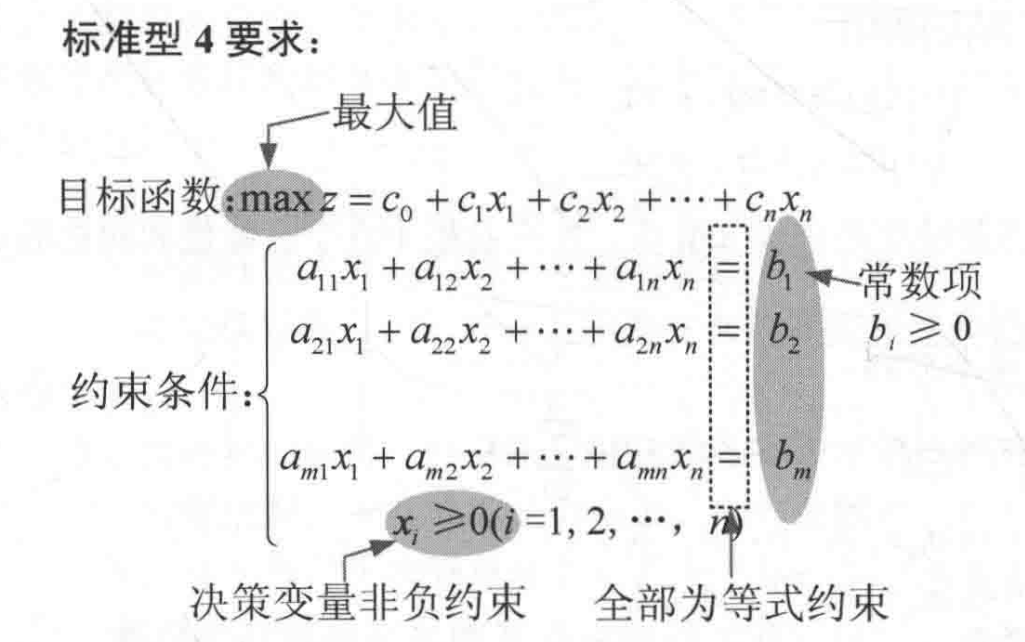

线性规划标准型转化方法

(1)一般线性规划形式中目标函数如果求最小值，即$\min z = \sum_{i=1}^n c_ix_i$，那么令$z’ = -z$，则求解$\max z’ = \sum_{i=1}^n c_ix_i$，得到最优解后加负号即可。
(2)右端常数项小于零时，则不等式两边同时乘-1，将其变为大于零，并改变不等式方向，保证恒等变形。
(3)约束条件大于等于约束时，则在不等式左边减去一个新的非负变量，将不等式约束改为等式约束。
(4)约束条件小于等于约束时，则在不等式左边加上一个新的非负变量，将不等式约束改为等式约束。
(5)无约束的决策变量x，则引入两个新的非负变量x’，x’’，令$x=x’-x’’, \ x’ \ge 0, \ x’’ \ge 0$，将x’，x’’带入模型
(6)决策变量x小于等于0时，令x’=-x，将x’带入模型

$$\min z = x_2 - 3 \ x_3 + 2 \ x_4$$
$$\begin{cases} x_1 + 3 \ x_2 - x_3 + 2 \ x_4 =7 \ -2 \ x_2 + 4 \ x_3 \le 12 \ -4 \ x_2 + 3 \ x_3 + 8 \ x_4 \le 10 \ x_i \ge 0 \ (i = 1, \ 2, \ 3, \ 4) \end{cases}$$
将其转化为线性规划标准型:z’=-z
$$\min z’ = -x_2 + 3 \ x_3 - 2 \ x_4$$
$$\begin{cases} x_1 + 3 \ x_2 - x_3 + 2 \ x_4 =7 \ -2 \ x_2 + 4 \ x_3 + x_5 = 12 \ -4 \ x_2 + 3 \ x_3 + 8 \ x_4 + x_6 = 10 \ x_i \ge 0 \ (i = 1, \ 2, \ 3, \ 4, \ 5, \ 6) \end{cases}$$

单纯行算法

基本变量：每个约束条件中的系数为正且只出现在一个约束条件中的变量
非基本变量：除基本变量外的变量全部为非基本变量
基本可行解：满足标准形式约束条件的可行解称为基本可行解
检验数：目标函数中非基本变量的系数

最优解的判别

(1)若目标函数中关于非基本变量的所有系数小于等于0，则当前基本可行解就是最优解。
(2)若目标函数中关于非基本变量的所有系数小于等于0，同时存在某个非基本变量的检验数等于0，则线性规划问题有无穷多个最优解。
(3)如果某个非基本变量的系数大于0，而该变量对应的列向量的各个分量都小于等于0，则该线性规划问题有无界解。

算法步骤

建立初始单纯形表

(1)从构建出的线性规划标准型中找出基本变量和非基本变量，且让目标函数由非基本变量表示。
(2)基本变量的系数要缩放到1，基本变量做列，非基本变量做行。
(2)检验数放第一行，常数项放第一列，约束条件中的非基本变量的系数作为值，构造初始单纯形表。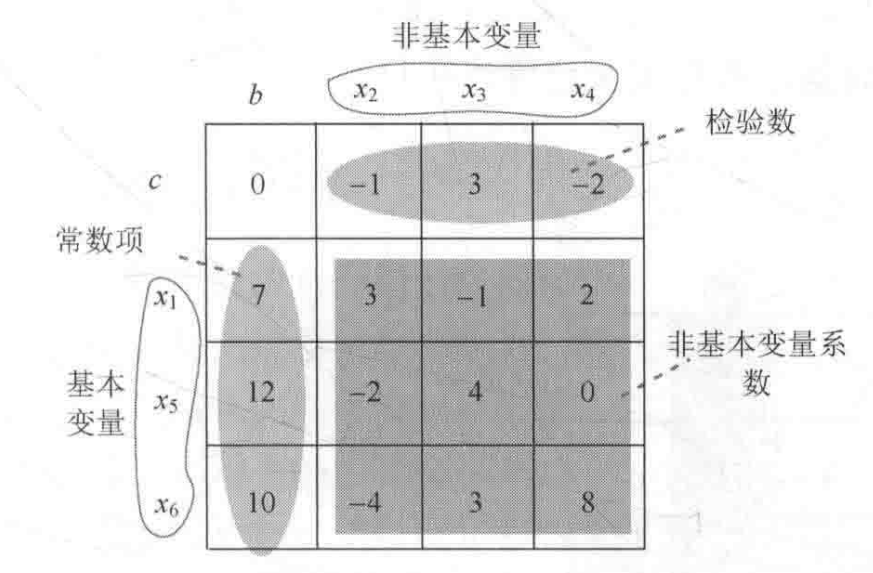

根据单纯形表判断是否得到最优解

(1)如果所有的检验数都小于等于0，则已获得最优解，算法结束，取出左上角的值即为最优解。
(2)如果所有的检验数有些为正数，但其中某一正的检验数对应的列向量的所有分量均小于等于0，则线性规划问题无解，算法结束。
(3)如果所有的检验数有些为正数，但其中某一正的检验数对应的列向量中有正的分量，则继续下一步。

选择入基变量

选取检验数中最大的一个，其对应的非基本变量称为入基变量，该列称为入基列

选择离基变量

选取常数列元素与入基列元素的比值中，正数的最小者所对应的基本变量为离基变量。

换基变换

将单纯形表上的入基变量和离基变量互换位置。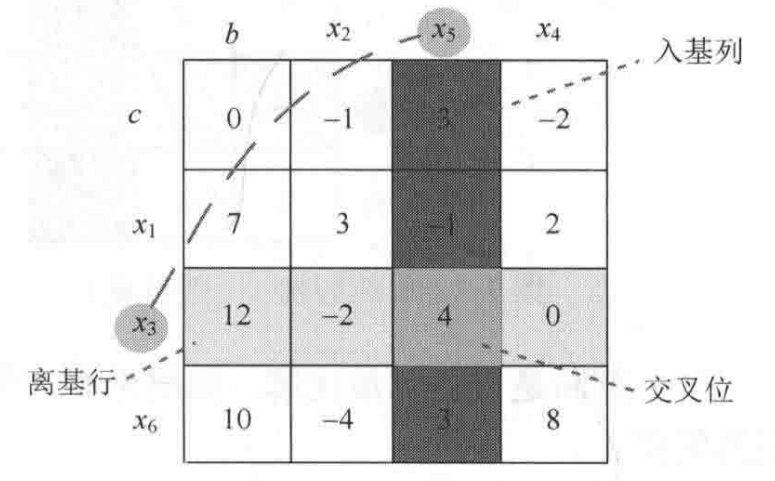

计算新的单纯形表

入基列=-原值/交叉位值。
离基行=原值/交叉位值。
交叉位=原值去倒数。
左上角值=原值+同行入基列元素值*同列离基行元素值/交叉位值。

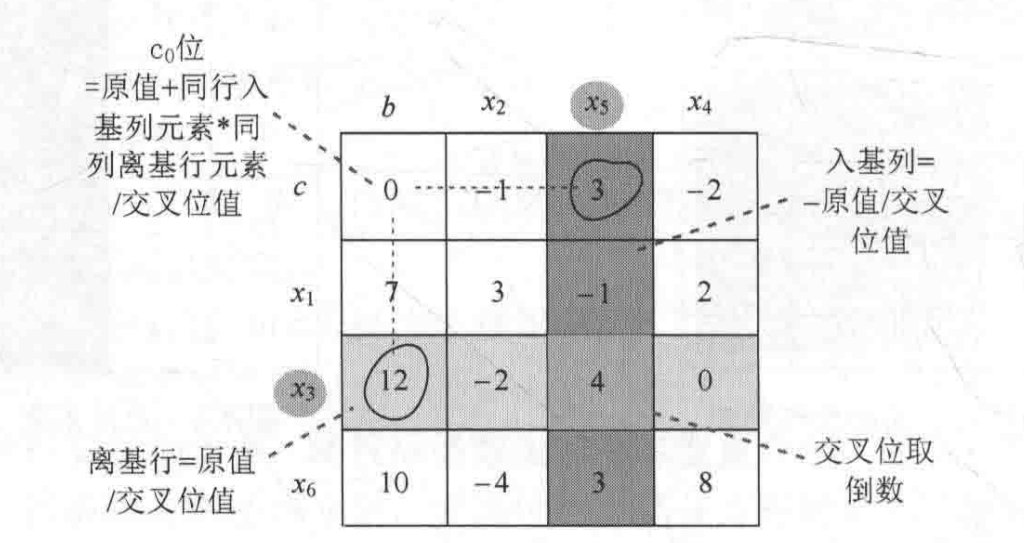
其余值=原值-同行入基列元素值*同列离基行元素值/交叉位值。

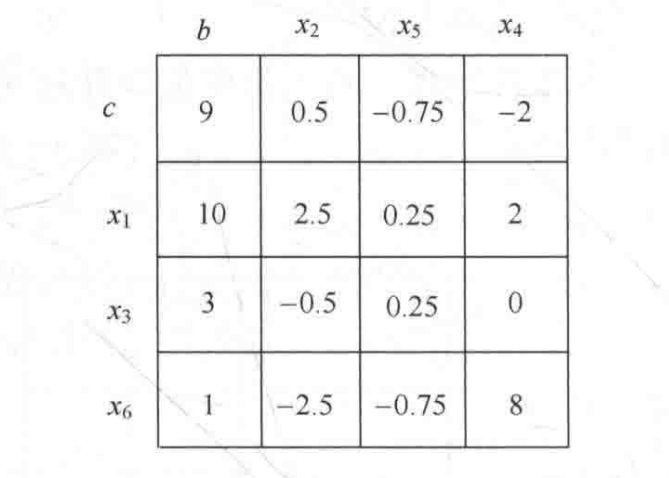
得到新的单纯形表再返回第二步重新判断。直到满足终止条件。
本题的最终的单纯形表如下，可知最优解为z’=11，由于此题要求最小值，即z=-z=-11。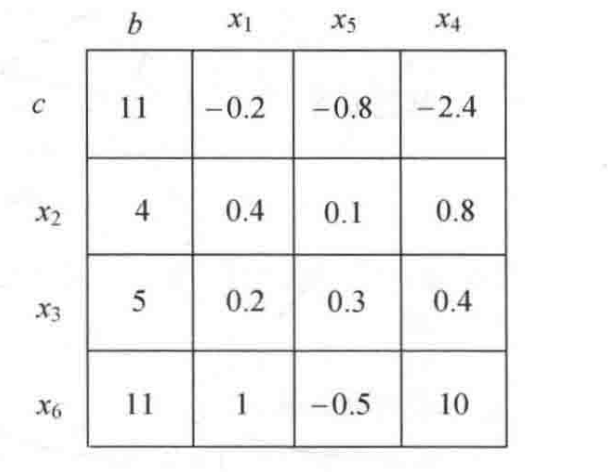

其最优解为基本变量对应的常数项组成，非基本变量全部置为0，即解为
$$\begin{pmatrix} x_1 \ x_2 \ x_3 \ x_4 \ x_5 \ x_6 \end{pmatrix} = \begin{pmatrix} 0 \ 4 \ 5 \ 0 \ 0 \ 11 \end{pmatrix}$$

经典例题(最大利润)

问题描述

某工厂有3个车间，第一个车间用1个单位的原料N可以加工5个单位的产品A和2个单位的产品B。
如果产品A直接售出，售价为10元，如果在第二个车间继续加工，则需要加工费5元，加工后售价为19元。
如果产品B直接售出，售价为16元，如果在第三个车间继续加工，则需要加工费4元，加工后售价为24元。
原材料N的单位购入价为5元，每工时的工资是15元，第一个车间加工一个单位的N需要0.05个工时，第二个车间加工一个单位需要0.1个工时，第三个车间加工一个单位需要0.08个工时。
每个月最多能得到12000单位的原材料N，工时最多为1000工时，问如何安排生产才能得到最高的收益？

问题分析

假设A直接卖出的数量为x₁，收获的利润为$10 \ x_1$
假设A在第二车间加工后的出售量为x₂，收获的利润为$(19-5-0.1 \times 15) \ x_2 = 12.5 \ x_2$
假设B直接卖出的数量为x₃，收获的利润为$16 \ x_3$
假设B在第三车间加工后的出售量为x₄，收获的利润为$(24-4-0.08 \times 15) \ x_4 = 18.8 \ x_4$
假设所用的原材料数量为x₅，所用的成本为$(5+0.05 \times 15) \ x_5 = 5.75 \ x_5$
根据分析可得目标函数和约束条件如下:
$$\max z = 10 \ x_1 + 12.5 \ x_2 + 16 \ x_4 +18.8 \ x_4 - 5.75 \ x_5$$
$$\begin{cases} x_1 + x_2 - 5 \ x_5 =0 \ x_3 + x_4 - 2 \ x_5 = 0 \ x_5 \le 12000 \ 0.1 \ x_1 + 0.08 \ x_4 +0.05 \ x_5 \le 1000 \ x_i \ge 0 \ (i = 1, \ 2, \ 3, \ 4, \ 5) \end{cases}$$

将其转换为标准型可知:
$$\max z = 10 \ x_1 + 12.5 \ x_2 + 16 \ x_4 +18.8 \ x_4 - 5.75 \ x_5$$
$$\begin{cases} x_1 + x_2 - 5 \ x_5 =0 \ x_3 + x_4 - 2 \ x_5 = 0 \ x_5 + x_6 = 12000 \ 0.1 \ x_1 + 0.08 \ x_4 +0.05 \ x_5 + x_7 = 1000 \ x_i \ge 0 \ (i = 1, \ 2, \ 3, \ 4, \ 5, \ 6, \ 7) \end{cases}$$

找出基本变量$x_1, \ x_3, \ x_6, \ x_7$和非基本变量$x_2, \ x_4, \ x_5$
将目标函数由非基本变量表示，即用$x_1 = 5 \ x_5 - x_2, \ x_3 = 2 \ x_5 - x_4$替换，目标函数转化为:
$$\begin{align} z & =10(5 \ x_5 - x_2) + 12.5 \ x_2 + 16(2 \ x_5 - x_4) + 18.8 \ x_4 - 5.75 \ x_5 \ & = 2.5 \ x_2 + 2.8 \ x_4 + 76.25 \ x_5 \ \end{align}$$

构造初始单纯形表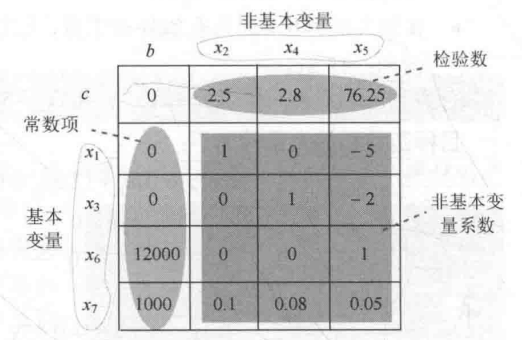

第一行输入基本变量的下标，第二行输入非基本变量的下标，然后输入初始单纯形表。

1 3 6 7 # 基本变量下标
2 4 5 # 非基本变量下标
0 2.5 2.8 76.25 # 初始单纯形表
0 1 0 -5
0 0 1 -2
12000 0 0 1
1000 0.1 0.08 0.05

python代码实战

import sys

def display_simplex_table(simplex_table):
    print('-----单纯形表如下-----')
    print(' '.join([' '] + nonbase_subscript))
    for i in range(base_num):
        print(' '.join([base_subscript[i]] + [str(x) for x in simplex_table[i]]))

def judge_simplex_table(simplex_table):
    global solve
    display_simplex_table(simplex_table)
    all_negative_j_flag = True
    for j in range(1, nonbase_num):
        if simplex_table[0][j] > 0:
            all_negative_j_flag = False
            all_negative_i_flag = True
            for i in range(1, base_num):
                if simplex_table[i][j] > 0:
                    all_negative_i_flag = False
            if all_negative_i_flag:
                print('该线性规划问题无界，无法求得最优解')
                return
    if all_negative_j_flag:
        for i in range(1, base_num):
            solve.append(base_subscript[i] + '=' + str(simplex_table[i][0]))
        for j in range(1, nonbase_num):
            solve.append(nonbase_subscript[j] + '=' + str(simplex_table[0][j]))
        print('该问题的最优解为:', simplex_table[0][0])
        print('该问题的解向量为:', ', '.join(solve))
        return
    else:
        update_simplex_table(simplex_table)
        return

def update_simplex_table(simplex_table):
    global base_subscript, nonbase_subscript
    in_base_var = simplex_table[0][1:].index(max(simplex_table[0][1:])) + 1
    ratio = []
    for i in range(1, base_num):
        ratio = ratio + [0]  if simplex_table[i][in_base_var] == 0 else ratio + [simplex_table[i][0]/simplex_table[i][in_base_var]]
    out_base_value = max(ratio) + 1
    out_base_var = 0
    for i in range(len(ratio)):
        out_base_value, out_base_var = [ratio[i], i] if 0 < ratio[i] < out_base_value else [out_base_value, out_base_var]
    out_base_var += 1
    tmp_table = [[0 for i in range(nonbase_num)] for j in range(base_num)]
    for i in range(base_num):
        for j in range(nonbase_num):
            if i == 0 and j == 0:
                tmp_table[i][j] = simplex_table[i][j] + simplex_table[out_base_var][j] * simplex_table[i][in_base_var] / simplex_table[out_base_var][in_base_var]
                continue
            if i != out_base_var and j != in_base_var:
                tmp_table[i][j] = simplex_table[i][j] - simplex_table[out_base_var][j] * simplex_table[i][in_base_var] / simplex_table[out_base_var][in_base_var]
                continue
            if i != out_base_var and j == in_base_var:
                tmp_table[i][j] = -1 * simplex_table[i][j] / simplex_table[out_base_var][in_base_var]
                continue
            if i == out_base_var and j != in_base_var:
                tmp_table[i][j] = simplex_table[i][j] / simplex_table[out_base_var][in_base_var]
                continue
            if i == out_base_var and j == in_base_var:
                tmp_table[i][j] = 1 / simplex_table[i][j]
                continue
    simplex_table = [x[:] for x in tmp_table]
    base_subscript[out_base_var], nonbase_subscript[in_base_var] = nonbase_subscript[in_base_var], base_subscript[out_base_var]
    judge_simplex_table(simplex_table)

print('输入基本变量下标:')
for line in sys.stdin:
    base_subscript = ['c'] + ['x' + x for x in line.strip().split()]
    print('输入非基本变量下标:')
    nonbase_subscript = ['b'] + ['x' + x for x in sys.stdin.readline().strip().split()]
    base_num, nonbase_num = len(base_subscript), len(nonbase_subscript)
    simplex_table, solve = [], []
    print('请输入初始单纯形表:')
    for i in range(base_num):
        simplex_table.append([float(x) for x in sys.stdin.readline().strip().split()])
    judge_simplex_table(simplex_table)

代码运行结果

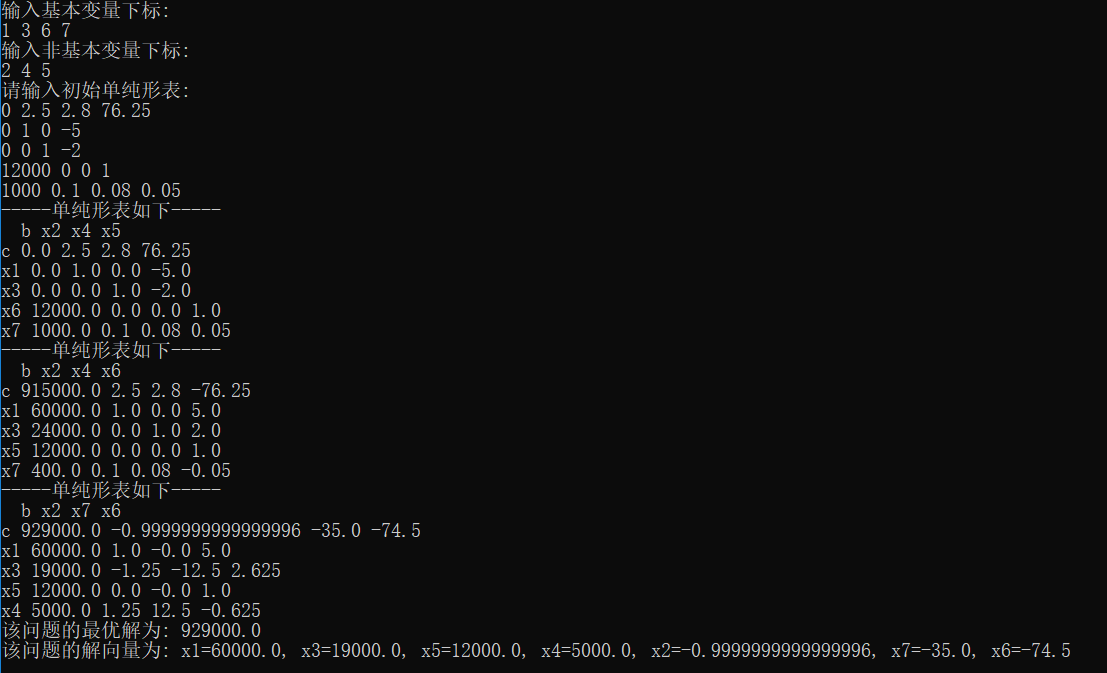
算法总结

线性规划问题的难点不在于算法的设计，而是在于如何从文字描述中寻找到合适的模型，如何建立线性规划方程组。线性规划在实际的生产生活中有着重要的应用，虽然该算法理解起来较为复杂，但是记住其求解形式，遇到此类问题直接仿照使用即可。