网络流(Network Flows)

发表于 | 分类于 ， | | 本文总阅读数 次
| 字数统计: 2.9k | 阅读时长 ≈ 12
Network Flows

网络流

原理介绍

   Network Flows:网络流，是运筹学中的最优化问题，也是图论中的一种理论方法。类比水流的解决问题，与线性规划密切相关，常常用来解决实际的生活问题。

1

算法基础

图的基本术语

  (1)无向图：G中的每条边都是没有方向的，顶点v1和v2之间的边记为(v1,v2)或(v2,v1)。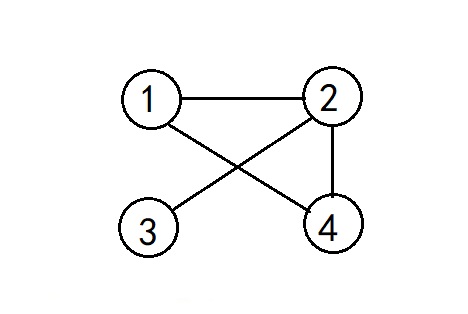
2
  (2)有向图：G中的每条边都是有方向的，顶点v1和v2之间的边记为<v1,v2>，不能写成<v2,v1>。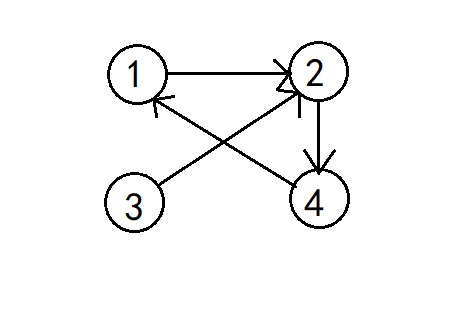
3
  (3)网：在边上标注距离，时间，花费等等数值，称为边的权值，带有权值的图称为网。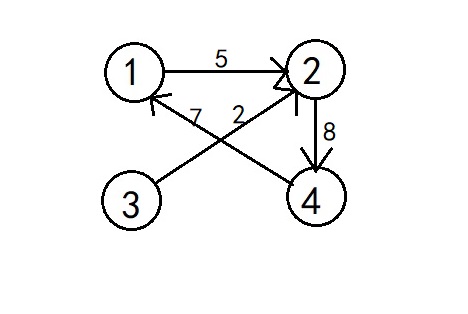
4
  (4)二分图：如果顶点集V可分割为两个互不相交的子集V1,V2，并且图中的每条边所对应的两个顶点分别属于这两个不同的顶点集，称G为二分图。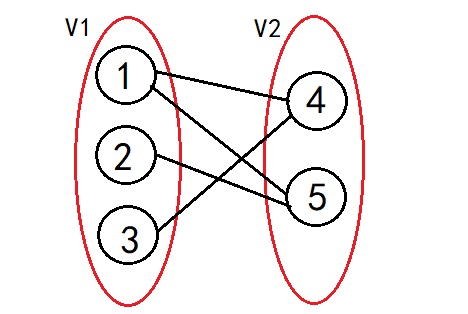
5

网络的基本术语

  (1)网络：在有向网中，有两个特殊的点，源点s和汇点t，图中各边的方向表示允许的流向，边上的权值表示可允许的最大流量，且两个结点之间最多只有一条边，称这样的图为网络。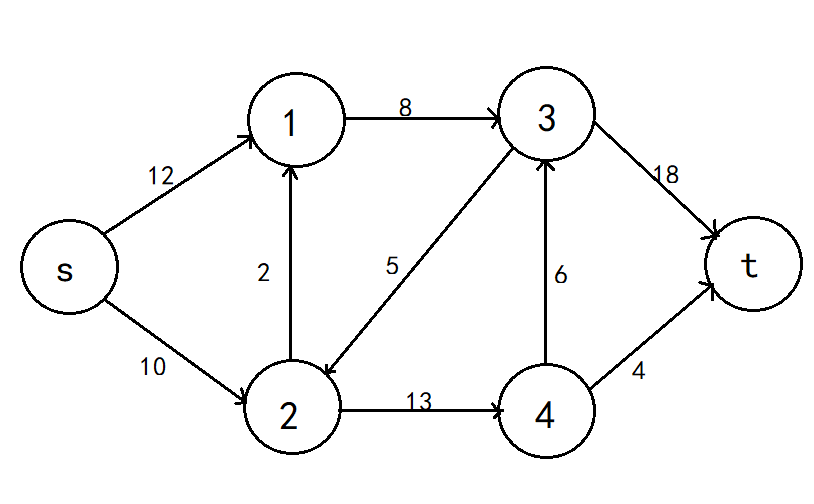
6
  (2)网络流：网络上的流，即定义在边集E上的非负函数flow称为网络流。
  (3)可行流：满足容量约束（每个边的实际流量不大于最大容量）和流量守恒（除了源点s和汇点t外，所有内部结点流入量等于流出量）两个性质的网络流称为可行流。
  (4)最大流：在满足可行流的条件下，在网络中找到一个净输出最大的网络流称为最大流。

经典例题(最大网络流，最短增广路算法)

问题描述

  一家公司要把一批货物从工厂运到北京，中间经过若干个城市，已知城市数，连接数和城市之间的最大运输量，求如何运输使运输量最大。
  第一行输入结点个数和边数，然后每行输入连通的两个城市以及最大运输量，使用空格分隔。

1
2
3
4
5
6
7
8
9
10
6 9 # 结点个数n和边数m
1 2 12 # 说明1号城市和2号城市之间的最大运输量为12
1 3 10
2 4 8
3 2 2
3 5 13
4 3 5
4 6 18
5 4 6
5 6 4

算法分析

  如果一条边的容量为n，已经流出了m则该点最多可以正向流出(n-m)或者反向流入m，因此引入一个残余网络，正向代表可增量，即还可以流出的容量，反向代表流量，即已经流出的容量，等于可以流入的流量。
12
  利用深度优先或者广度优先从源点s对该图进行遍历，如果从i点到达j点的值大于0，说明可以流通，则继续。当搜索到t点时，说明该路径是一条可行流，找到该路径上边的最小值，最大流加上该值，然后修改网络，将路径上的边正向减去该值，反向加上该值。重新搜索，直到无法到达t点算法结束。

python代码实战

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
import sys
import pandas as pd

def sap(connect_map, n):
    real_map = [[0 for i in range(n + 1)] for j in range(n + 1)]
    residue_map = [[x for x in row] for row in connect_map]
    max_flow, find_flag = 0, True
    while find_flag:
        queue, find_flag = [[1, [1]]], False
        while queue:
            i, route = queue.pop(0)
            for j in range(1, n + 1):
                if residue_map[i][j] > 0 and j not in route:
                    if j == n:
                        flow, route, queue, find_flag = [], route + [j], [], True
                        for k in range(len(route) - 1):
                            flow.append(residue_map[route[k]][route[k + 1]])
                        min_flow = min(flow)
                        max_flow += min_flow
                        for p in range(len(route) - 1):
                            real_map[route[p]][route[p + 1]] += min_flow
                            residue_map[route[p]][route[p + 1]] -= min_flow
                            residue_map[route[p + 1]][route[p]] += min_flow
                        break
                    else:
                        queue.append([j, route + [j]])
    return real_map, max_flow

print('请输入结点个数n和边数m:')
for line in sys.stdin:
    n, m = [int(x) for x in line.strip().split()]
    connect_map, label, direction = [[0 for i in range(n + 1)] for j in range(n + 1)], ['v' + str(i) for i in range(1, n + 1)], []
    print('请输入结点个数u,v及边u-v的容量w:')
    for i in range(m):
        u, v, w = [int(x) for x in sys.stdin.readline().strip().split()]
        connect_map[u][v] = w
        direction.append([u, v])
    real_map, max_flow = sap(connect_map, n)
    for k in direction:
        real_map[k[0]][k[1]] -= real_map[k[1]][k[0]]
        real_map[k[1]][k[0]] = 0
    net_work = pd.DataFrame([[x for x in row[1:]] for row in real_map[1:]], index=label, columns=label)
    print('网络的最大流值为:', max_flow, '\n---------实流网络如下:---------\n', net_work)

代码运行结果

14

经典例题(最大网络流，重贴标签算法)

问题描述

  一家公司要把一批货物从工厂运到北京，中间经过若干个城市，已知城市数，连接数和城市之间的最大运输量，求如何运输使运输量最大。
  第一行输入结点个数和边数，然后每行输入连通的两个城市以及最大运输量，使用空格分隔。

1
2
3
4
5
6
7
8
9
10
6 9 # 结点个数n和边数m
1 2 12 # 说明1号城市和2号城市之间的最大运输量为12
1 3 10
2 4 8
3 2 2
3 5 13
4 3 5
4 6 18
5 4 6
5 6 4

算法分析

  在上例算法中，浪费了许多时间，因为要从源点重复进行深度优先遍历或者广度优先遍历，因此有重复的大量计算。
  引入混合网络，将残余网络进行优化，同向边为一个元组(cap, flow)记录容量和当前流量，反向边也是一个元组(0, -flow)记录容量个当前流量，可以通过该网络直接看出方向和流量。
13
  (1)从汇点开始，利用广度优先算法对结点添加标签，从0开始，第一次直接访问到的点标记为1，第二次间接访问到的点标记为2，依次贴标签。
  (2)如果源点高度大于等于结点数，说明已经找到了最大流，算法结束，否则从源点开始，搜索源点高度-1的点，观察是否可以前进，如果可以，当结点为汇点时，进行增流减流操作(同向边增流，反向边减流)，如果不可以则需要重贴标签。
  (3)重贴标签：如果拥有当前结点高度的结点只有一个，则算法结束，否则寻找是否有可行邻接边(容量大于流量)，如果有则令当前结点高度等于邻接点高度的最小值+1，否则令当前结点的高度等于结点数。重新回到(2)

python代码实战

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
import sys
import pandas as pd

def isap(mix_net, height_table, n):
    max_flow, real_map = 0, [[0 for i in range(n + 1)] for j in range(n + 1)]
    while height_table[1] < n:
        current_node, stack = 1, []
        while current_node != n:
            next_height, flag, index = height_table[current_node] - 1, False, 0
            for i in range(1, n + 1):
                if height_table[i] == next_height and mix_net[current_node][i][0] > mix_net[current_node][i][1]:
                    flag, index = True, i
                    break
            if flag:
                stack.append(current_node)
                current_node = index
                if current_node == n:
                    stack.append(current_node)
                    flow = []
                    for k in range(len(stack) - 1):
                        flow.append(mix_net[stack[k]][stack[k + 1]][0] - mix_net[stack[k]][stack[k + 1]][1])
                    min_flow = min(flow)
                    max_flow += min_flow
                    for p in range(len(stack) - 1):
                        real_map[stack[p]][stack[p + 1]] += min_flow
                        mix_net[stack[p]][stack[p + 1]][1] += min_flow
                        mix_net[stack[p + 1]][stack[p]][1] -= min_flow
            else:
                if height_table.count(height_table[current_node]) == 1:
                    return real_map, max_flow
                min_neibor, no_neibor = n, True
                for i in range(1, n + 1):
                    if mix_net[current_node][i][0] > mix_net[current_node][i][1]:
                        no_neibor, min_neibor = False, min(min_neibor, height_table[i])
                height_table[current_node] = n if no_neibor else min_neibor + 1
                if stack:
                    current_node = stack[-1]
                    stack.pop()
                else:
                    current_node = 1
    return real_map, max_flow


def init_height(queue):
    global height_table
    while queue:
        j, height = queue.pop(0)
        for i in range(1, n + 1):
            if mix_net[i][j][0] > 0 and height_table[i] == -1:
                height_table[i] = height + 1
                queue.append([i, height + 1])


print('请输入结点个数n和边数m:')
for line in sys.stdin:
    n, m = [int(x) for x in line.strip().split()]
    mix_net, label, height_table, direction = [[[0, 0] for i in range(n + 1)] for j in range(n + 1)], ['v' + str(i) for i in range(1, n + 1)], [-1] * n + [0], []
    print('请输入结点个数u,v及边u-v的容量w:')
    for i in range(m):
        u, v, w = [int(x) for x in sys.stdin.readline().strip().split()]
        mix_net[u][v], mix_net[v][u] = [w, 0], [0, 0]
        direction.append([u, v])
    init_height([[n, 0]])
    real_map, max_flow = isap(mix_net, height_table, n)
    for k in direction:
        real_map[k[0]][k[1]] -= real_map[k[1]][k[0]]
        real_map[k[1]][k[0]] = 0
    net_work = pd.DataFrame([[x for x in row[1:]] for row in real_map[1:]], index=label, columns=label)
    print('网络的最大流值为:', max_flow, '\n---------实流网络如下:---------\n', net_work)

代码运行结果

15

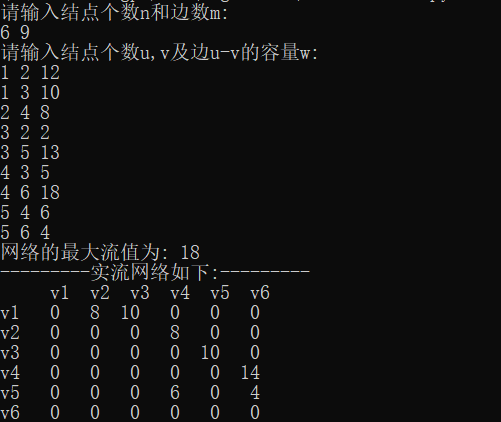
经典例题(最小费用最大流)

问题描述

  一家公司要把一批货物从工厂运到北京，中间经过若干个城市，已知城市数，连接数和城市之间的最大运输量，以及单位货物的运送费用，如何找到一种流量最大费用尽可能小的方法。
  第一行输入结点个数和边数，然后每行输入连通的两个城市以及最大运输量，和单位货物运输费用，使用空格分隔。

1
2
3
4
5
6
7
8
9
10
11
6 10 # 结点个数n和边数m
1 2 3 1 # 说明1号城市和2号城市之间的最大运输量为3，单位运输量费用为1
1 3 4 7
2 3 1 1
2 4 6 4
2 5 4 5
3 4 5 3
3 5 3 6
4 6 7 6
5 4 3 3
5 6 3 2

算法分析

  (1)最短增广路算法类似，先建立混合网络。
  (2)从源点开始搜索，找到一条最短费用路，如果无法搜索到汇点，则算法结束，已经找到最小费用最大流，否则总花费加上该路径边上的最小值乘路径上的所有花费之和作为目前的总花费。
  (3)然后更新混合网络，正向增流，反向减流。回到步骤(2)

python代码实战

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
import sys
import pandas as pd

def spfa(mix_net, n):
    real_map = [[0 for i in range(n + 1)] for j in range(n + 1)]
    max_flow, total_cost, find_flag, min_cost, min_route = 0, 0, True, 65535, [1]
    while min_route:
        queue, find_flag, min_cost, min_route = [[1, [1], 0]], False, 65535, []
        while queue:
            i, route, cost = queue.pop(0)
            if i == n and min_cost > cost:
                min_cost, min_route = cost, route
            for j in range(1, n + 1):
                if mix_net[i][j][0] > mix_net[i][j][1] and j not in route:
                    queue.append([j, route + [j], cost + mix_net[i][j][2]])
        if min_route:
            flow = []
            for k in range(len(min_route) - 1):
                flow.append(mix_net[min_route[k]][min_route[k + 1]][0] - mix_net[min_route[k]][min_route[k + 1]][1])
            min_flow = min(flow)
            max_flow += min_flow
            total_cost += min_cost * min_flow
            for p in range(len(min_route) - 1):
                real_map[min_route[p]][min_route[p + 1]] += min_flow
                mix_net[min_route[p]][min_route[p + 1]][1] += min_flow
                mix_net[min_route[p + 1]][min_route[p]][1] -= min_flow
    return real_map, max_flow, total_cost


print('请输入结点个数n和边数m:')
for line in sys.stdin:
    n, m = [int(x) for x in line.strip().split()]
    mix_net, label, direction = [[[0, 0, 0] for i in range(n + 1)] for j in range(n + 1)], ['v' + str(i) for i in range(1, n + 1)], []
    print('请输入结点个数u，v及边u-v的容量w，单位容量费用c:')
    for i in range(m):
        u, v, w, c = [int(x) for x in sys.stdin.readline().strip().split()]
        mix_net[u][v], mix_net[v][u] = [w, 0, c], [0, 0, -c]
        direction.append([u, v])
    real_map, max_flow, total_cost = spfa(mix_net, n)
    for k in direction:
        real_map[k[0]][k[1]] -= real_map[k[1]][k[0]]
        real_map[k[1]][k[0]] = 0
    net_work = pd.DataFrame([[x for x in row[1:]] for row in real_map[1:]], index=label, columns=label)
    print('网络的最大流值为:', max_flow, '\n网络的最小费用为:', total_cost, '\n---------实流网络如下:---------\n', net_work)

代码运行结果

16

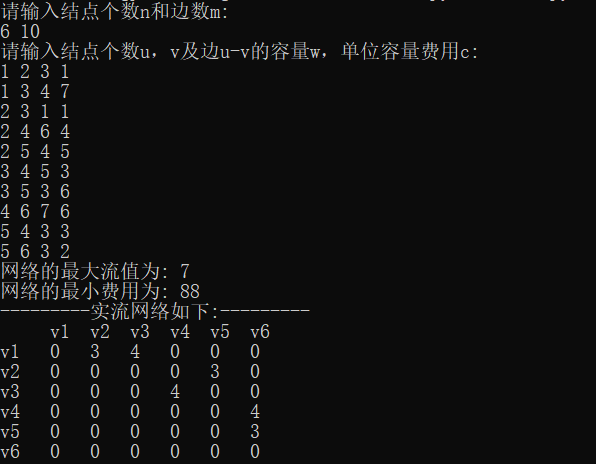
算法总结

  网络流是一种较为复杂的算法，通常用来解决实际的问题，其模板固定，难点在于如何将问题转化为一个网络流表示的形式，因此需要多加练习，做到熟练掌握。

-------------本文结束感谢您的阅读-------------
0%