二叉树介绍
二叉树(Binary tree):是一种常见的数据结构,也是学习计算机必须要掌握的一种模型,与之相关的概念有很多,完全二叉树,二叉搜索树,二叉排序树,红黑树等等,相关的算法也有很多,深度优先搜索,广度优先搜索等等,今天的主要内容不在于此。有个朋友问我,二叉树有3种遍历方式,给出两种如何计算第三种,今天给小伙伴们理一理。
先序遍历(preorder traversal)
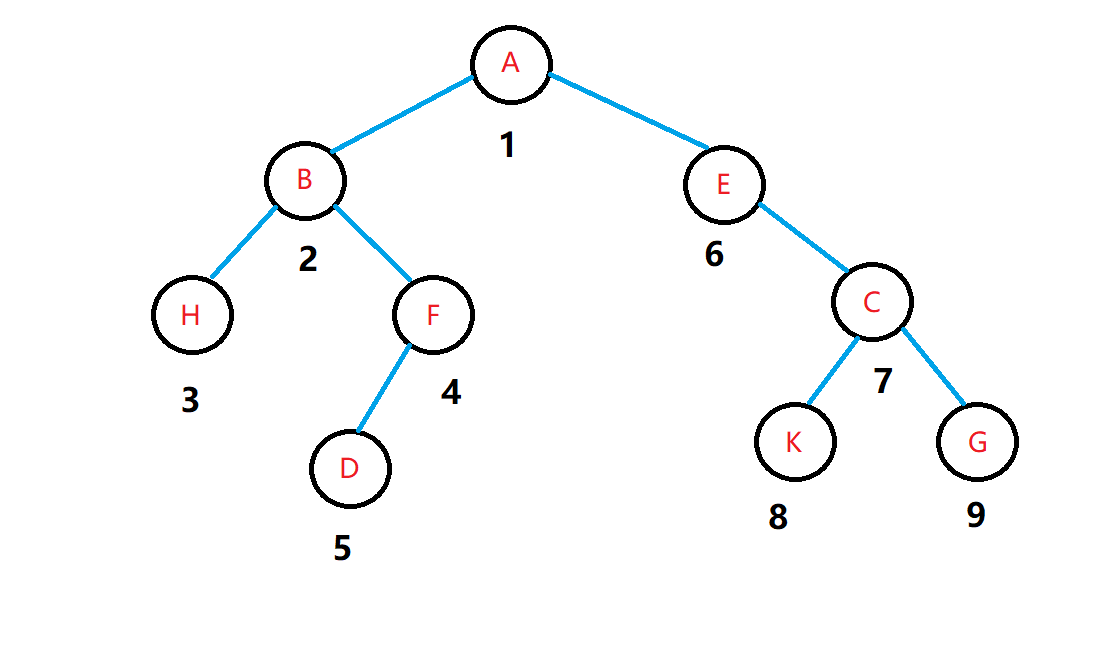
(1)访问根节点
(2)遍历左子树(在遍历左子树的时候也按照先序遍历)
(3)遍历右子树(在遍历右子树的时候也按照先序遍历)
中序遍历(inorder traversal)
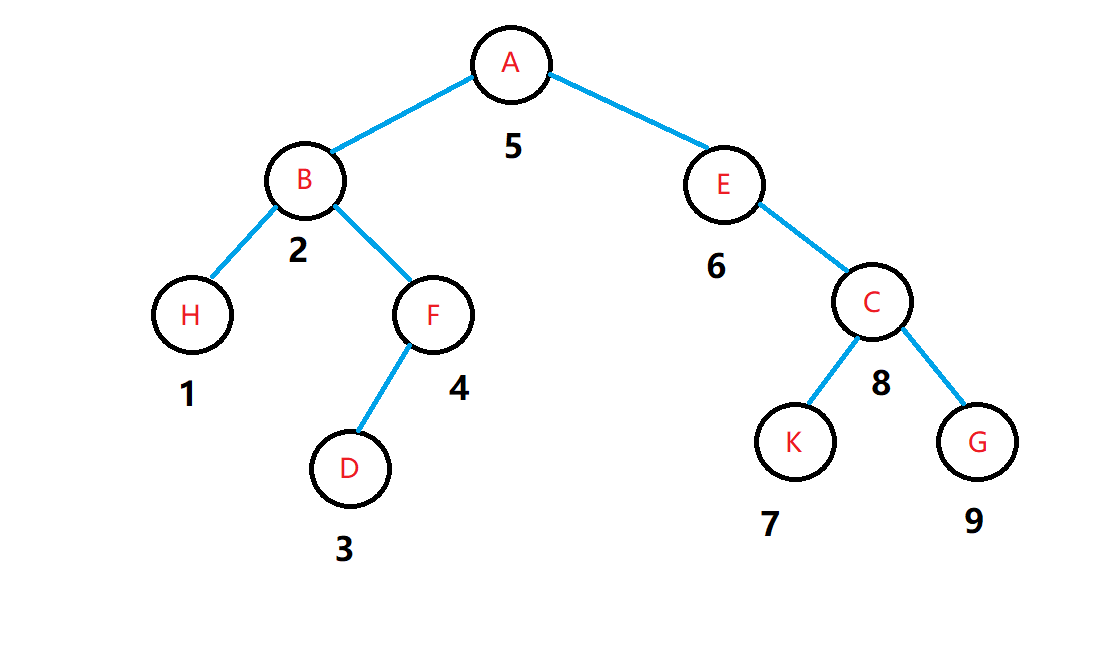
(1)遍历左子树(在遍历左子树的时候也按照中序遍历)
(2)访问根节点
(3)遍历右子树(在遍历右子树的时候也按照中序遍历)
后序遍历(postorder traversal)
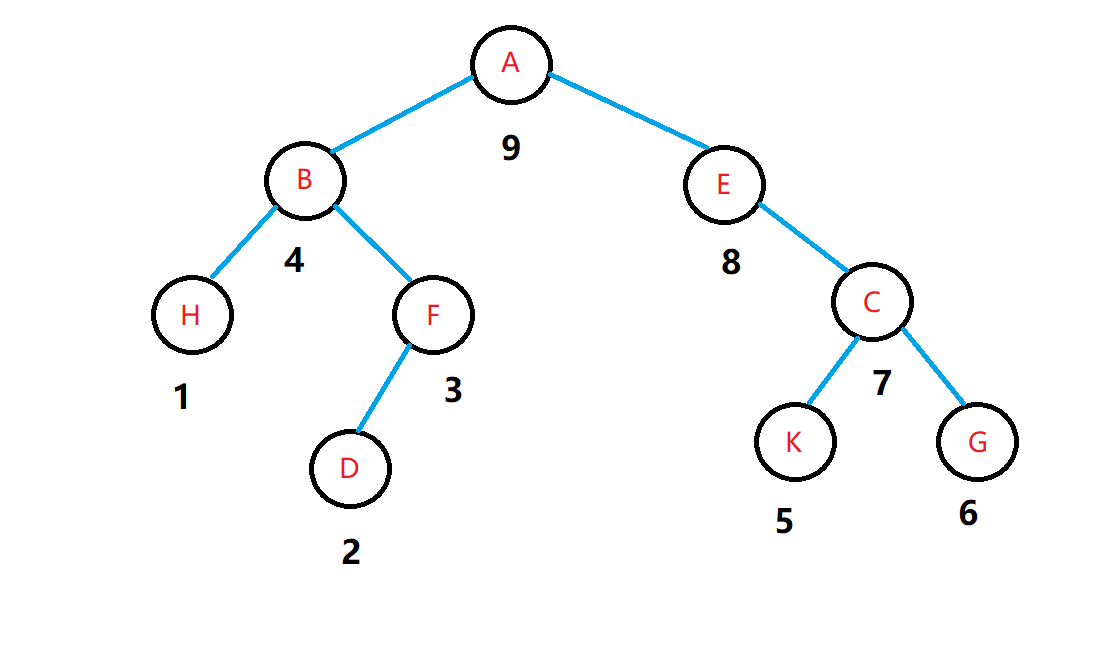
(1)遍历左子树(在遍历左子树的时候也按照后序遍历)
(2)遍历右子树(在遍历右子树的时候也按照后序遍历)
(3)访问根节点
给定先序和中序,求解后序遍历
先序遍历,因为先访问根节点,因此可以得出第一个节点就是根节点。
中序遍历,先访问左子树,然后访问根节点,因此根节点之前的都是根节点的左子树,根节点之后的都是根节点的右子树。
从根节点的左子树中进行迭代,重复上述过程。
就以上面这个情况为例,先序遍历的结果是ABHFDECKG,中序遍历的结果是HBDFAEKCG,我们进行分析。
- 先序可以知道根节点A,在中序遍历中A之前为HBDF是A的左子树,A之后为EKCG为A的右子树。
- 从HBDF中寻找根节点,在先序遍历中,B是HBDF中第一个出现的节点,因此B是根节点,在中序遍历中B之前为H是B的左子树,B之后为DF是B的右子树。
- 从DF中寻找根节点,在先序遍历中,F是DF中第一个出现的节点,因此F是根节点,在中序遍历中F之前为D是F的左子树。F没有右子树。此时A的左子树全部遍历完毕。
- 从EKCG中寻找根节点,在先序遍历中,E是EKCG中第一个出现的节点,因此E是根节点,在中序遍历中E之前没有节点,E没有左子树,E之后为KCG是E的右子树。
- 从KCG中寻找根节点,在先序遍历中,C是KCG中第一个出现的节点,因此C是根节点,在中序遍历中C之前为K是左子树,C之后为G是右子树。此时遍历结束。
- 通过之前的遍历,可以重建出这个树的全貌,因此再通过后序遍历读出节点顺序即可。结果为HDFBKGCEA,小伙伴们可以进行尝试能否推导出来。
给定中序和后序,求解先序遍历
后序遍历,因为最后访问根节点,因此可以得出最后一个节点就是根节点。
中序遍历,先访问左子树,然后访问根节点,因此根节点之前的都是根节点的左子树,根节点之后的都是根节点的右子树。
从根节点的左子树中进行迭代,重复上述过程。
就以上面这个情况为例,中序遍历的结果是HBDFAEKCG,后序遍历的结果是HDFBKGCEA,我们进行分析。
- 后序可以知道根节点A,在中序遍历中A之前为HBDF是A的左子树,A之后为EKCG为A的右子树。
- 从HBDF中寻找根节点,在后序遍历中,B是HBDF中最后一个出现的节点,因此B是根节点,在中序遍历中B之前为H是B的左子树,B之后为DF是B的右子树。
- 从DF中寻找根节点,在后序遍历中,F是DF中最后一个出现的节点,因此F是根节点,在中序遍历中F之前为D是F的左子树。F没有右子树。此时A的左子树全部遍历完毕。
- 从EKCG中寻找根节点,在后序遍历中,E是EKCG中第一个出现的节点,因此E是根节点,在中序遍历中E之前没有节点,E没有左子树,E之后为KCG是E的右子树。
- 从KCG中寻找根节点,在后序遍历中,C是KCG中第一个出现的节点,因此C是根节点,在中序遍历中C之前为K是左子树,C之后为G是右子树。此时遍历结束。
- 通过之前的遍历,可以重建出这个树的全貌,因此再通过先序遍历读出节点顺序即可。结果为ABHFDECKG,小伙伴们也可以进行尝试能否推导出来。
给定先序和后序,求解中序遍历
这个是无法求解的,因为已知先序和后序,出现了过多的信息冗余,导致有效信息不足,以上题来说,先序的第一个节点一定是A,那么后序的最后一个节点也一定是A,这就是无效信息,下图展示了一个极端的例子。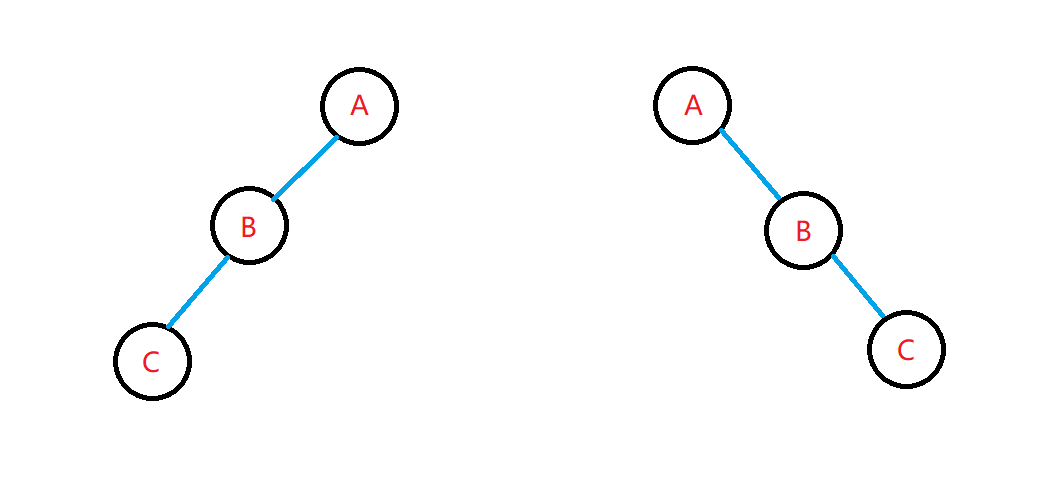
在这个图中,小伙伴们可以写一下它们的先序遍历和后序遍历,就会发现它们的先序遍历和后序遍历都是一样的,因为它们只有左子树或者只有右子树,可以将左子树和右子树看成一个整体,因此两个遍历的结果是相同的,所以不能够通过先序和后序得出树得全貌。
小结
树的遍历是经典的笔试考题,掌握小伙伴的基本功力,因此小伙伴们一定要学习如何通过两种遍历得到另一种遍历的过程。