题目分析

这道题目简单来说就是一个字符串匹配问题，看起来很简单，但是想要降低时间复杂度较为困难。可以通过暴力法或者KMP方法求解。

暴力法

暴力法很好理解，长度已经给定，穷举所有可能的子串，并且与模板字符串比较，如果相等则输出出现的位置，否则输出-1即可，时间复杂度为O((N-L)L)，空间复杂度为O(1)，其中N为原始字符串长度，L为模板字符串长度。

class Solution:
    def strStr(self, haystack, needle):
        """
        :haystack: str
        :needle: str
        :rtype: int
        """
        lens = len(needle)
        for i in range(len(haystack) - lens + 1):
            if haystack[i:i + lens] == needle:
                return i
        return -1

KMP

KMP算法是一种专门解决字符串匹配的算法，因为暴力法浪费了太多的比较次数，尤其是前面的字符都匹配正确后，最后一个字符匹配失败，又要从头开始匹配，效率太低，而KMP算法可以完成O(N)的时间复杂度和O(L)的空间复杂度。

我们借用一下leetcode题解中宫水三叶(叶神)的图举例。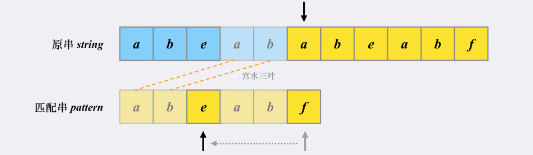

class Solution:
    def strStr(self, haystack, needle):
        """
        :haystack: str
        :needle: str
        :rtype: int
        """

        def getNext(pattern):
            next = [-1] * len(pattern)
            i, j = 0, -1
            while i < len(pattern) - 1:
                if j == -1 or pattern[i] == pattern[j]:
                    i += 1
                    j += 1
                    next[i] = j
                else:
                    j = next[j]
            return next

        next = getNext(needle)
        i, j = 0, 0
        while i < len(haystack) and j < len(needle):
            if j == -1 or haystack[i] == needle[j]:
                i += 1
                j += 1
            else:
                j = next[j]
        if j >= len(needle):
            return i - len(needle)
        else:
            return -1

class Solution {
    private int tl;

    private int pl;

    public int strStr(String t, String p) {
        tl = t.length();
        pl = p.length();
        int[] next = getNext(p);
        int i = 0;
        int j = 0;
        while (i < tl && j < pl) {
            if (j == -1 || t.charAt(i) == p.charAt(j)) {
                i++;
                j++;
            } else {
                j = next[j];
            }
        }
        return j == pl ? i - pl : -1;
    }

    private int[] getNext(String p) {
        int[] next = new int[pl];
        Arrays.fill(next, -1);
        int i = 0;
        int j = -1;
        while (i < pl - 1) {
            if (j == -1 || p.charAt(i) == p.charAt(j)) {
                next[++i] = ++j;
            } else {
                j = next[j];
            }
        }
        return next;
    }
}

字符串哈希

这个题目事隔两年多，2022年11月又来打卡了，这次再提供一个新颖的解法——字符串哈希。

不妨设长度为k的字符串s = [c0, c1, c2, c3… ck-1]，哈希值为

$$ hashcode(s_k) = c_0 \times b^{k - 1} + c_1 \times b^{k - 2} + c_2 \times b^{k - 3} + … + c_{k - 1} $$

记pattern的哈希是hashcode，长度为pl，而template的哈希需要动态去计算，因为pattern可能是template的一部分，即从m开始，则长度为pl的字符串的哈希值为

$$ hashcode(p_{m-(m + pl - 1)}) = c_m \times b^{pl - 1} + c_{m+1} \times b^{pl - 2} + c_{m + 2} \times b^{pl - 3} + c_{m + pl - 1} $$

两个字符串的哈希值如果相等，可以认为两个字符串相等(后面会进行解释)。如果对每一个位置都计算，则时间复杂度和暴力是一样的。

所以引入前缀和的思想，从索引0开始到m + pl的字符串哈希值为
$$ hashcode(p_{m + pl - 1}) = c_0 \times b^{m + pl - 1} + c_1 \times b^{m + pl - 2} + … + c_{m - 1} \times b^{pl} + c_m \times b^{pl - 1} + … + c_{m + pl - 1} $$

$$ hashcode(p_{m - 1}) = c_0 \times b^{m - 1} + c_1 \times b^{m - 2} + … + c_{m - 1} $$

根据上述两式可得
$$ hashcode(p_{m + pl - 1}) - hashcode(p_{m - 1}) \times b^{pl} = hashcode(p_{m-(m + pl - 1)}) $$

则从i开始长度为pl的hashcode可以表示为hashcode[i + pl] - hashcode[i] x b^pl，并比较这个值和pattern的哈希值是否相等即可。

这里有个问题，哈希值相等，结果就一定相等吗？
答案是不一定的，哈希会存在冲突，要计算b^pl次方，如果b是偶数，那么次方用int表示可能会导致结果为0。因为超过int表示，就会MOD 2^31。

因此b的选择一般为偶数，且为了防止哈希冲突，b会选择超过字符集的大小

超过字符集的目的是，尽量保证高位不相等时，结果不相等。
比如za和ab这两个字符串，如果选择b = 25，那么za = 25 + 0 x 25 = 25，ab = 0 + 1 x 25 = 25，那么就会冲突，导致错误结果。

本题是小写字母，字符集大小为26，因为26是偶数，那么选择27就是可以的。

这里还要注意一点：并不是选择27一定是可以的，因为curSum不是完全单调递增的，超过int32的最大值，就会变成负数，因此还是有极低的概率存在哈希冲突。此时如果没有通过，可以尝试更换b即可。

算法的时间复杂度为O(n)，空间复杂度为O(n)。

class Solution {
    public int strStr(String t, String p) {
        int tl = t.length();
        int pl = p.length();
        int[] curSum = new int[tl + 1];
        int base = 1;
        int factor = 27;
        for (int i = 1; i <= tl; i++) {
            curSum[i] = curSum[i - 1] * factor + t.charAt(i - 1) - 'a';
        }
        int hashcode = 0;
        for (int i = 0; i < pl; i++) {
            base *= factor;
            hashcode = hashcode * factor + p.charAt(i) - 'a';
        }
        for (int i = 0; i <= tl - pl; i++) {
            int j = i + pl;
            int curHashcode = curSum[j] - curSum[i] * base;
            if (curHashcode == hashcode) {
                return i;
            }
        }
        return -1;
    }
}

刷题总结

字符串匹配问题是一个经典的问题，大多数学校或者数据结构算法课中都作为例子进行讲解，但是很难讲的非常透彻，因为这个问题太抽象，在这里我只能用文字进行描述，所以描述的可能更不清晰，小伙伴们以要理解我举得例子，尤其是j = Next[j]这一步，可以说是KMP问题的精髓，看懂了这一步基本上就可以明白算法具体在做什么了。这次又补充了字符串哈希的方法，后面也会讲解一些字符串哈希的题目，可以在本站点直接搜索字符串哈希，会检索到所有字符串哈希的题目。