Activation黑科技

Activation

背景介绍

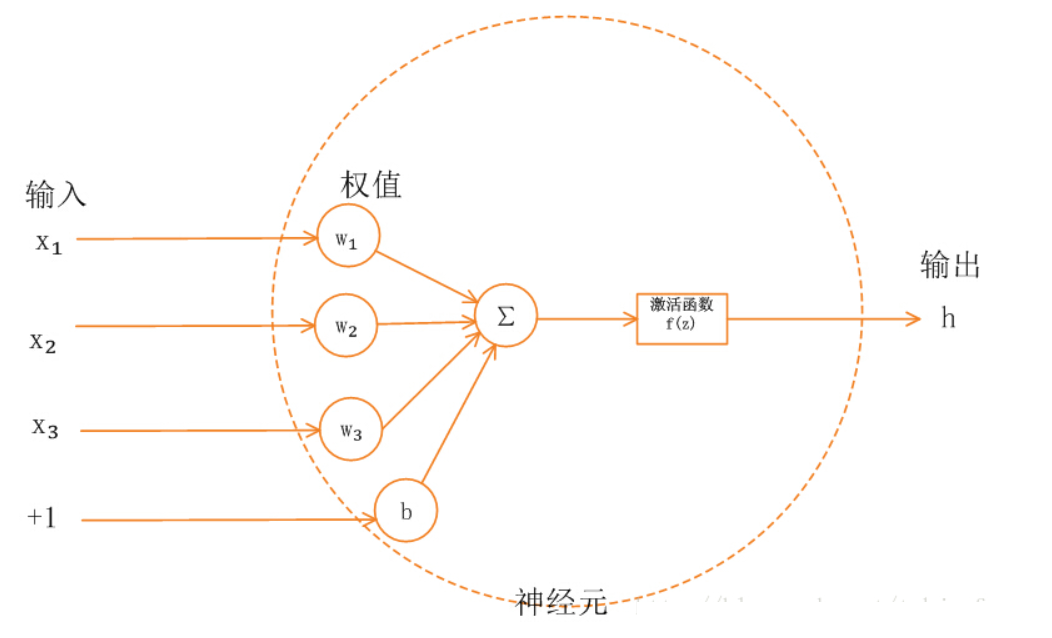
  Activation(激活函数):在多层神经网络中，上层节点的输出和下层节点的输入之间具有一个函数关系，这个函数称为激活函数。如果不用激活函数每一层节点的输入都是上层输出的线性函数，很容易验证，无论你神经网络有多少层，输出都是输入的线性组合，与没有隐藏层效果相当，这样会导致网络的逼近能力大大降低，所以需要引入非线性函数作为激活函数，这样可以提高神经网络的表达能力，可以逼近任意函数，不再是输入的线性组合。

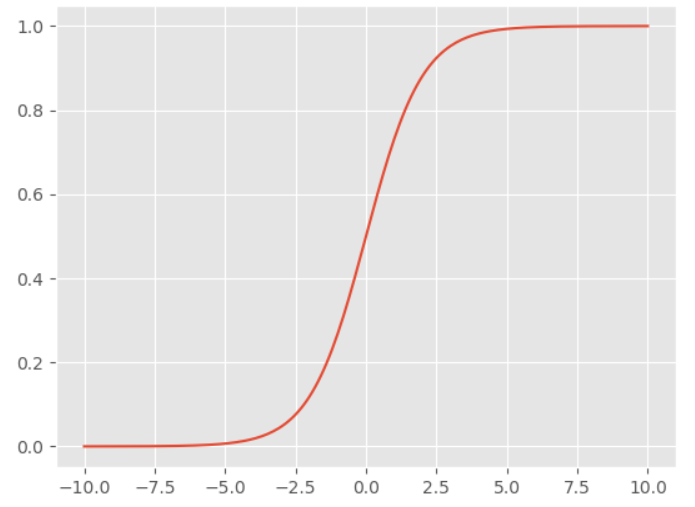
Sigmoid激活函数

$$f(z) = \frac{1}{1+e^{-z}}$$
在TensorFlow2.0中的实现

import tensorflow.keras as keras
import numpy as np
import matplotlib.pyplot as plt


def plot(x, y):
    plt.plot(x, y)
    plt.show()

plt.style.use('ggplot')
x = np.linspace(-10, 10, 201)
y = keras.activations.sigmoid(x)
plot(x, y)

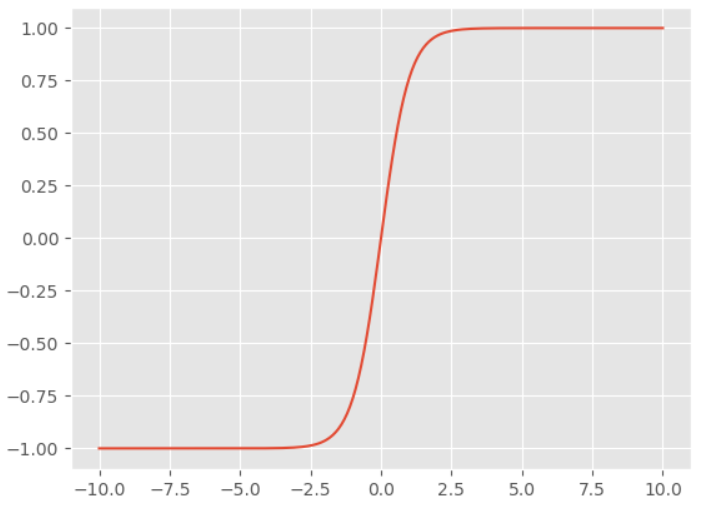
tanh激活函数

$$f(x) = \frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}$$
在TensorFlow2.0中的实现

import tensorflow.keras as keras
import numpy as np
import matplotlib.pyplot as plt


def plot(x, y):
    plt.plot(x, y)
    plt.show()

plt.style.use('ggplot')
x = np.linspace(-10, 10, 201)
y = keras.activations.tanh(x)
plot(x, y)

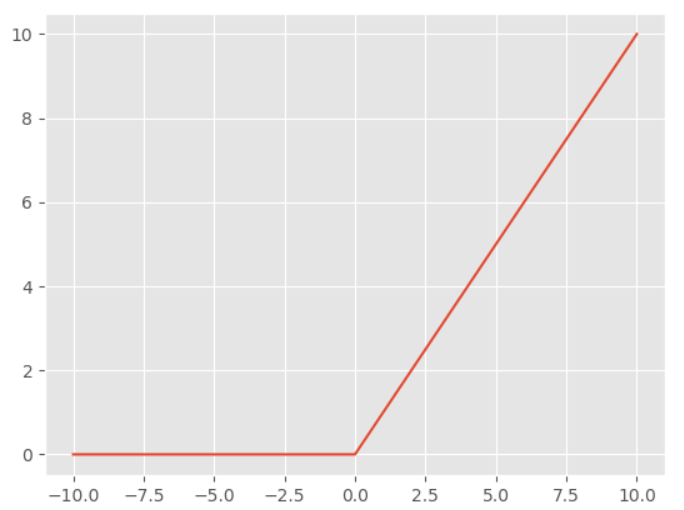
ReLU激活函数

$$f(x) = \max(0, x)$$
在TensorFlow2.0中的实现

import tensorflow.keras as keras
import numpy as np
import matplotlib.pyplot as plt


def plot(x, y):
    plt.plot(x, y)
    plt.show()

plt.style.use('ggplot')
x = np.linspace(-10, 10, 201)
y = keras.activations.relu(x)
plot(x, y)

Leaky-ReLU激活函数

$$f(x) = \max(\alpha x, x), \alpha=0.01$$
在TensorFlow2.0中的实现

import tensorflow.keras as keras
import numpy as np
import matplotlib.pyplot as plt


def plot(x, y):
    plt.plot(x, y)
    plt.show()

plt.style.use('ggplot')
x = np.linspace(-10, 10, 201)
y = keras.activations.relu(x, alpha=0.01)
plot(x, y)

PReLU激活函数

$$f(x) = \max(\alpha x, x)$$
PReLU和Leaky-ReLU的表达式是相同的，区别在于Leaky-ReLU中的 $$\alpha$$ 是预先设定的，而PReLU中的参数是根据数据，通过网络自身学习的。TensorFlow2.0中直接提供了PReLU层

import tensorflow.keras as keras


keras.layers.layers.PReLU()

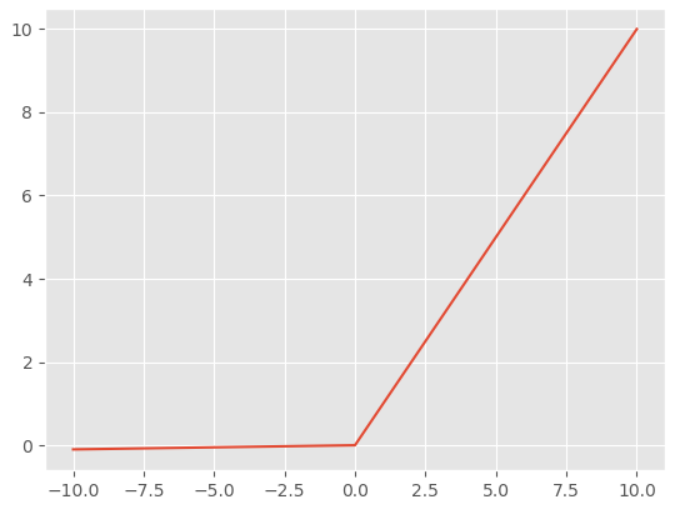
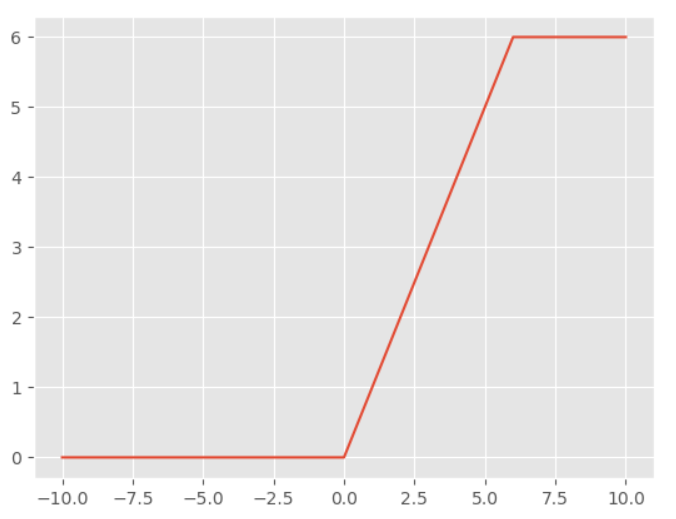
ReLU6激活函数

$$f(x) = \min(6, \max(0, x))$$
在TensorFlow2.0中的实现

import tensorflow.keras as keras
import numpy as np
import matplotlib.pyplot as plt


def plot(x, y):
    plt.plot(x, y)
    plt.show()

plt.style.use('ggplot')
x = np.linspace(-10, 10, 201)
y = keras.activations.relu(x, max_value=6)
plot(x, y)

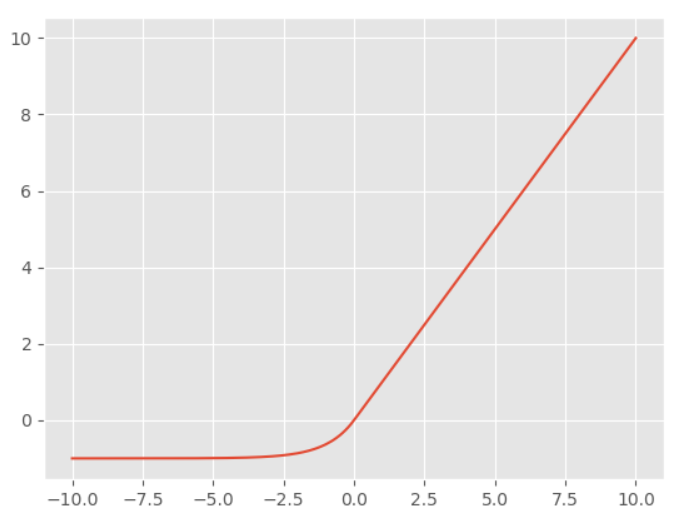
ELU激活函数

$$f(x) = \begin{cases} x & x > 0 \\ \alpha(e^{x} - 1) & x \le 0 \end{cases}, \alpha=1$$
在TensorFlow2.0中的实现

import tensorflow.keras as keras
import numpy as np
import matplotlib.pyplot as plt


def plot(x, y):
    plt.plot(x, y)
    plt.show()

plt.style.use('ggplot')
x = np.linspace(-10, 10, 201)
y = keras.activations.elu(x, alpha=1)
plot(x, y)

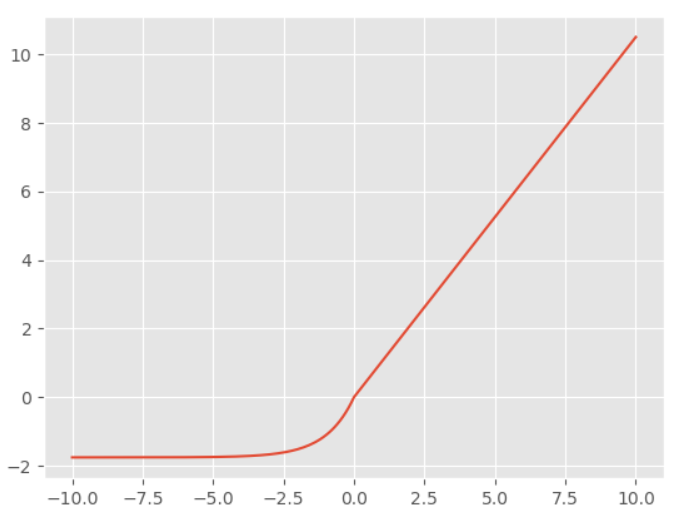
SELU激活函数

$$f(x) = \lambda \begin{cases} x & x > 0 \\ \alpha(e^{x} - 1) & x \le 0 \end{cases}$$
$$\begin{cases} \lambda=1.0507009873554804934193349852946 \\ \alpha=1.6732632423543772848170429916717 \end{cases}$$
在TensorFlow2.0中的实现，在SELU函数中，经过大量论证后，两个参数都为定值，因此不需要设置参数。

import tensorflow.keras as keras
import numpy as np
import matplotlib.pyplot as plt


def plot(x, y):
    plt.plot(x, y)
    plt.show()

plt.style.use('ggplot')
x = np.linspace(-10, 10, 201)
y = keras.activations.selu(x)
plot(x, y)

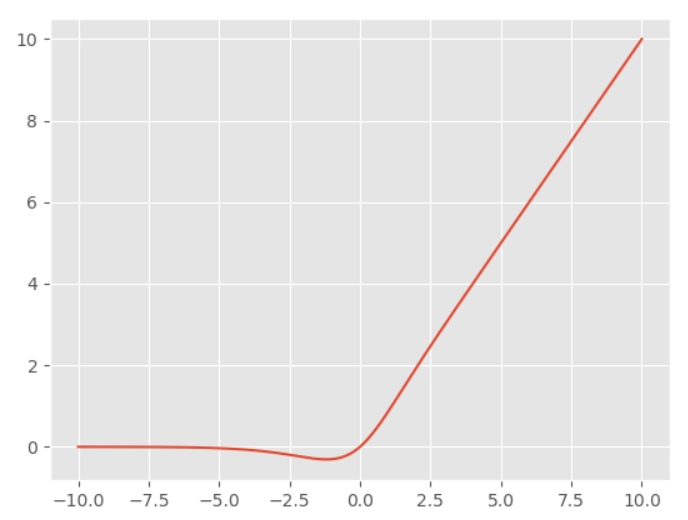
Mish激活函数

$$f(x) = x * tanh(\ln{(1+e^x)})$$
综合了tanh和Softplus的优点，类似于ReLU函数，但是对负值有轻微的梯度，其平滑的特点可能允许更好的信息深入神经网络，几乎在所有的问题上都有很好的表现，在TensorFlow2.0中的实现。

import tensorflow.keras as keras
import numpy as np
import matplotlib.pyplot as plt


def plot(x, y):
    plt.plot(x, y)
    plt.show()

plt.style.use('ggplot')
x = np.linspace(-10, 10, 201)
y = x * keras.activations.tanh(keras.activations.softplus(x))
plot(x, y)

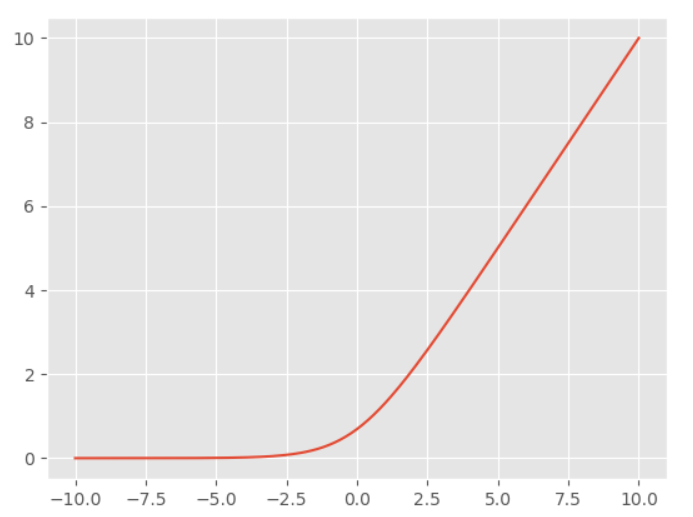
Softplus激活函数

$$f(x) = \ln{(1+e^x)}$$
在TensorFlow2.0中的实现

import tensorflow.keras as keras
import numpy as np
import matplotlib.pyplot as plt


def plot(x, y):
    plt.plot(x, y)
    plt.show()

plt.style.use('ggplot')
x = np.linspace(-10, 10, 201)
y = keras.activations.softplus(x)
plot(x, y)

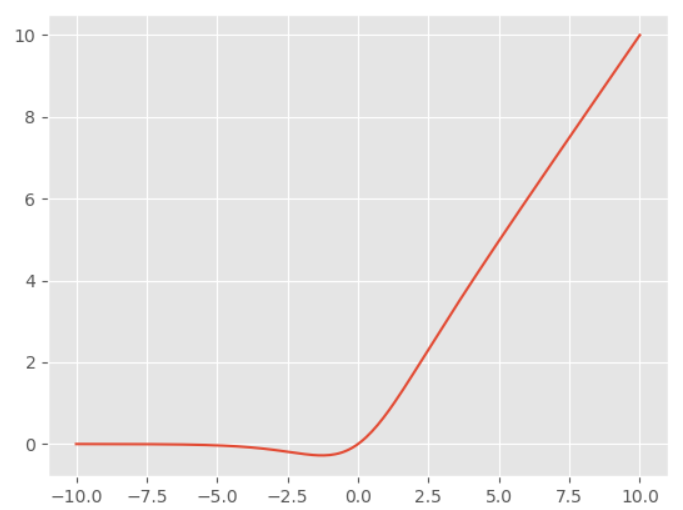
Swish激活函数

$$f(x) = x * sigmoid(x)$$
在TensorFlow2.0中的实现

import tensorflow.keras as keras
import numpy as np
import matplotlib.pyplot as plt


def plot(x, y):
    plt.plot(x, y)
    plt.show()

plt.style.use('ggplot')
x = np.linspace(-10, 10, 201)
y = x * keras.activations.sigmoid(x)
plot(x, y)

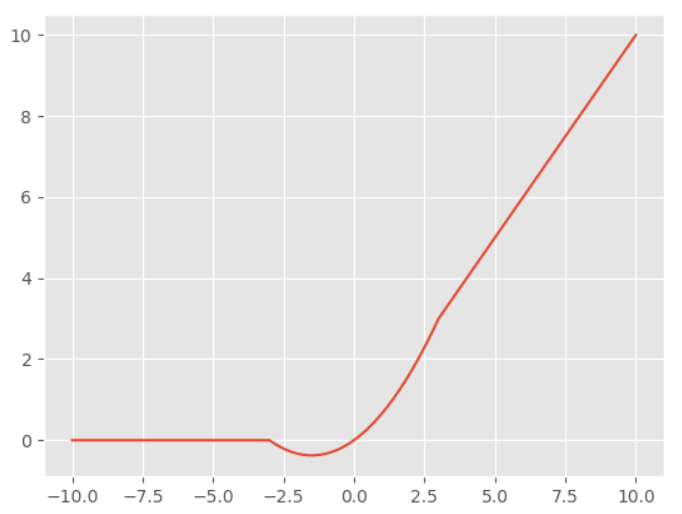
H-Swish激活函数

$$f(x) = x * \frac{ReLU6(x + 3)}{6}$$
在TensorFlow2.0中的实现

import tensorflow.keras as keras
import numpy as np
import matplotlib.pyplot as plt


def plot(x, y):
    plt.plot(x, y)
    plt.show()

plt.style.use('ggplot')
x = np.linspace(-10, 10, 201)
y = x * keras.activations.relu(x + 3, max_value=6) / 6
plot(x, y)

Softmax激活函数

$$\sigma_{i}(z) = \frac{e^{z_i}}{\sum_{j=1}^{m}{e^{z_j}}}$$
在TensorFlow2.0中的实现，和其他的激活函数不同，Softmax激活函数需要指定一个维度，而且使用时也必须先转化为大于一维的tensor形式，numpy格式的数据无法直接使用。

import tensorflow as tf
import tensorflow.keras as keras


x = tf.constant([[10, 1, 1, 1]], tf.float32)
y = keras.activations.softmax(x)

优缺点比较

Sigmoid函数优点：Sigmoid函数处处连续，处处可导。且能够控制数值的幅度，不会产生很大的变化，可以作为二分类任务的输出，而ReLU类型的激活函数对大于0的值几乎没有约束。
Sigmoid函数缺点：饱和区的神经元会产生梯度消失现象，使得学习速度大大下降，并且指数函数计算耗时。
tanh函数优点：tanh函数和Sigmoid类似，但是可以发现tanh的导数的值域为(0, 1]，而Sigmoid的导数的值域为(0, 0.25]，因此相当于延迟了饱和周期。
tanh函数缺点：tanh函数和Sigmoid类似，也具有梯度消失问题，和指数计算耗时问题。
ReLU类函数优点：ReLU类型函数(ReLU6，Leaky_ReLU，PReLU，SELU，ELU，Mish，Softplus)会使一部分神经元为0或者非常小，使得网络具有稀疏性，减少了参数的相互依赖关系，缓解了过拟合，而且ReLU函数及其导数的计算非常简单。
ReLU类函数缺点：可能存在神经元坏死现象，在x<0的时候，梯度为0，可能会使这个神经元很难再被激活，且ReLU函数不能控制参数的幅度，可能会产生梯度爆炸现象。
Swish类函数优点：Swish函数是介于ReLU函数和Sigmoid函数之间的一种平滑函数，具有两者的优点，不会像Sigmoid函数一样产生饱和区，也不会像ReLU函数一样存在坏死神经元。
Swish类函数缺点：Swish函数也具有两者的缺点，类似于Sigmoid函数计算耗时，类似于ReLU函数难以控制参数幅度，但整体表现较好。
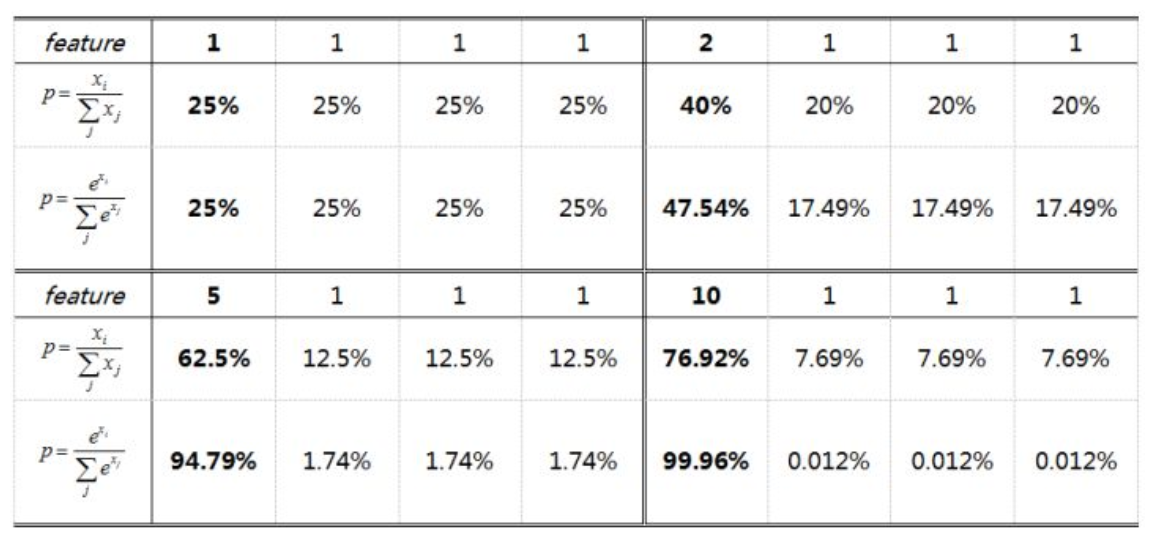
Softmax函数特点：Softmax函数和其他的激活函数不同，Softmax主要用于多分类任务中，如图像分割，目标检测，需要判断某一个像素或者某一个预测框属于哪一个类别。Softmax将输入归一化到[0, 1]之间，并且保证和为1，使人能够联想到概率的条件，也是属于[0, 1]，并且和为1。加上指数的作用是增加样本之间的差距，如果输入为90个1和1个10，则直接归一化的结果为90个0.01和1个0.1，如果10是对应的类别，即使已经分类的较好，仍然会使得误差较大。加上指数运算后，归一化的结果为90个0.000122，1个0.989，这样误差就会较小，更加接近于真实的情况。

激活函数的选择

1. 首先判断任务类型，是分类任务，回归任务，还是作为隐藏层非线性单元，如果是多分类任务则考虑Softmax激活函数，如果是二分类任务则考虑Sigmoid，tanh激活函数，如果是回归任务则可以考虑不加激活函数，因为激活函数可能会对回归的数据产生限制，如果是隐藏层非线性单元则考虑Sigmoid，tanh，ReLU，Swish等等。
2. 如果是隐藏层非线性单元，首先尝试ReLU激活函数，如果ReLU效果欠佳则考虑ReLU变种激活函数，ReLU6，Leaky_ReLU，SELU，ELU，Mish，Softplus等等
3. 如果效果不好，再考虑Swish类函数和Sigmoid，tanh函数，但是如果发现梯度消失问题，则避免使用Sigmoid和tanh函数。
4. 如果都不好用，则考虑是否网络结构，超参数，损失函数设计出现问题。

小结

  深度学习工程问题是一类非常复杂的问题，往往需要网络结构，超参数，损失函数，激活函数相互配合工作，可能某个结构或者某个参数适合某个激活函数，而另外的结构适合其他激活函数。因此需要小伙伴们在实际的工程任务中慢慢摸索，多多尝试。