背景介绍
Loss(损失函数):在深度学习任务中,一个最重要的概念就是损失函数,这里不区分损失函数,代价函数和目标函数,这里指的就是神经网络中最终需要优化的函数。损失函数决定者参数更新的方向,神经网络的输出y_pred要和真实值y_true进行比较,使两者的距离越小越好,这个距离的度量就是损失函数。打一个简单的比方,损失函数对于神经网络来说就有如灯塔之于船只,可以指明前进的方向。神经网络的参数更新是根据损失函数来确定的,如果损失函数设置错误,则会产生巨大偏差,甚至南辕北辙的效果,在这篇博客中,我向大家介绍一些常用的损失函数。
MSE(Mean Squared Error,均方误差)
$$ MSE = \frac{1}{N} \sum_{i=1}^{N}{(y^{(i)} - f(x^{(i)}))^2} $$
MSE:指参数估计值与参数真值之差平方的期望值,其中**平方误差是估计值和实际值之差的平方,也称为(L2 Loss)**,MSE可以评价数据的变化程度,MSE的值越小,说明预测模型描述实验数据具有更好的精确度。在TensorFlow2.0中已经给我们提供了计算MSE的损失函数。
1 | import tensorflow as tf |
MAE(Mean Absolute Error,平均绝对误差)
$$ MAE = \frac{1}{N} \sum_{i=1}^{N}{|y^{(i)} - f(x^{(i)})|} $$
MAE:指参数估计值与参数真值绝对误差的平均值,其中**绝对误差是估计值和实际值之间的距离,也称为(L1 Loss)**,MAE能更好地反映预测值误差的实际情况。在TensorFlow2.0中已经给我们提供了计算MAE的损失函数。
1 | import tensorflow as tf |
Smooth L1 Loss(平滑L1损失)
$$ smooth_{L_1} = \begin{cases} 0.5x^2 & |x| < 1 \ |x| - 0.5 & |x| \ge 1 \end{cases} $$
MAE的优点:鲁棒性更好,如果误差大于1,MSE会将误差放大,因此对异常数据更加敏感,为了调整异常值会牺牲很多样本。
MSE的优点:稳定性更好,如果误差小于1,MSE会将误差缩小,产生一个较小的波动,可以更加细化模型,MAE可能会跳过这个微小区域,到达另一个误差更大的地方。
Smooth L1 Loss可以完美的结合MAE和MSE的优点,在误差大于1的情况下,不会放大误差牺牲样本,在误差小于1的情况下,还能够细化模型,因此是一种较好的损失函数,在目标检测算法中常常使用。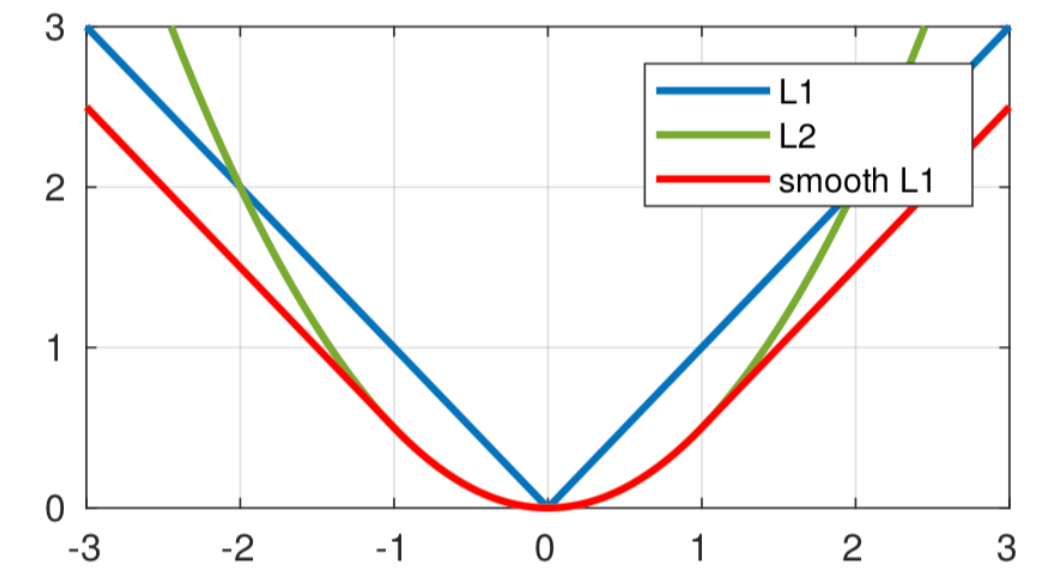
Binary Cross Entropy(二分类交叉熵损失函数)
$$ Binary \ Cross \ Entropy = -\frac{1}{N} \sum_{i=1}^{N}{(y^{(i)} \cdot \ln{(f(x^{(i)})}) + (1 - y^{(i)}) \cdot \ln{(1 - f(x^{(i)})})} $$
Binary Cross Entropy:用来评估当前训练得到的概率分布与真实分布的差异情况,它刻画的是实际概率与期望概率的距离,也就是交叉熵的值越小,两个概率分布就越接近,减少交叉熵损失就是在提高模型的预测准确率。在二分类中,每个数据独立计算交叉熵,和同一维度其他数据无关,允许多个1同时出现,经常配合sigmoid激活函数使用。在TensorFlow2.0中已经给我们提供了计算Binary Cross Entropy的损失函数。
1 | import tensorflow as tf |
Categorical Cross Entropy(多分类交叉熵损失函数)
$$ Categorical \ Cross \ Entropy = -\frac{1}{N} \sum_{i=1}^{N}{(y^{(i)} \cdot \ln{(f(x^{(i)})))}} $$
Categorical Cross Entropy:用来评估当前训练得到的概率分布与真实分布的差异情况,它刻画的是实际概率与期望概率的距离,也就是交叉熵的值越小,两个概率分布就越接近,减少交叉熵损失就是在提高模型的预测准确率。在多分类中,在某个维度上计算交叉熵,在该维度上其他数据一般只有一个1出现,其他全为0,经常配合Softmax激活函数使用。在TensorFlow2.0中已经给我们提供了计算Categorical Cross Entropy的损失函数。
1 | import tensorflow as tf |
Focal Loss(聚焦损失)
$$ Focal \ Loss = \begin{cases} - \alpha \cdot (1 - f(x^{(i)}))^{\gamma} \cdot \ln{(f(x^{(i)}))} & y^{(i)} = 1 \ - (1 - \alpha) \cdot (f(x^{(i)}))^{\gamma} \cdot \ln{(1 - f(x^{(i)}))} & y^{(i)} = 0 \end{cases} $$
Focal Loss(聚焦损失):是何凯明于2017年提出的一种解决目标检测算法中,一步法正负样本比例严重失衡的问题。他认为一步法和两步法的表现差异主要原因是大量背景类别导致的,因此设计了一个简单密集型网络RetinaNet来训练,保证速度的同时达到了精度最优。Focal Loss中有两个重要特点,引入$ \alpha $控制正负样本的权重,引入$ \gamma $控制容易分类和难分类样本的权重。
$ \alpha $:在这里称之为平衡因子,它的作用是平衡正负样本的占比,在论文中取0.25。为什么负样本多,反而占比还大呢?因为正样本比负样本更难区分,负样本为背景区域,较易区分,损失函数较小,因此占比较大。正样本难以区分,损失函数较大,因此占比较小。
$ \gamma $:在这里称之为调制权重,他的作用是关注分类的难易程度,在论文中取2。一个正样本,如果预测概率越大,则$1-f(x^{(i)})$越小,那么$(1-f(x^{(i)}))^{\gamma}$就更小,说明让网络不要过多关心容易区分的问题,反之,如果预测概率较小,则$1-f(x^{(i)})$较大,那么$(1-f(x^{(i)}))^{\gamma}$就相对较大,说明让网络多关心难区分的问题。
Focal Loss和Binary Cross Entropy:当参数满足$ \alpha=0.5,\gamma=0 $时Focal Loss就变成了Binary Cross Entropy,Binary Cross Entropy中一个正样本,预测结果为0.8时的损失为$- \ln{0.8}=0.223$,预测结果为0.2时的损失为$- \ln{0.2}=1.609$,两者相差8倍,而在Focal Loss中一个正样本,预测结果为0.8时的损失为$- 0.25 \times (1-0.8)^2 \times \ln{0.8}=0.00223$,预测结果为0.2时的损失为$- 0.25 \times (1-0.2)^2 \times \ln{0.2}=0.2575$,两者相差115倍,此时可以说网络更加关心预测为0.2时产生的损失,这就是Focal Loss受到广泛关注的特点。但是Tensorflow2.0没有给我们提供Focal Loss损失函数,需要我们自己设计。大家可以参考目标检测文章中RetinaNet中的相关内容,里面有Focal Loss的具体实现代码。
小结
在选择损失函数时,我们首先要判断任务类型,是分类任务还是回归任务。分类任务可以考虑交叉熵损失函数,回归任务可以考虑MSE或者MAE损失函数。但是在实际工程应用之中,往往不是一个简单的损失函数就能解决的,有时既用到分类损失函数,又用到回归损失函数,而且还要为两者之间设置权重系数。有时需要根据需要自己设计一些属于特殊数据集或者特殊模型的损失函数。因此需要小伙伴们多多尝试,总结经验,最终会成为一代大牛,