背景介绍

Optimizer(优化器):在深度神经网络中，如果说到达Loss最小是我们的终点站，那么出行方式就是优化器，它给我们提供一种方法接近Loss最小的地方。打一个简单的比方，如果我要从安徽前往北京，北京就是我们的目标，相当于神经网络中的Loss函数，而我们选择的交通方式则是优化器，我可以选择长途汽车出行，也可以选择火车出行，也可以选择飞机出行。选择哪一种交通方式最为合适呢？这也需要根据实际问题确定，优化器也是这样，没有最好的优化器，只有最适合的优化器，这里我不写太多的公式，主要是聊一聊各个优化器的用法，特点和参数表达的意义。

SGD(Stochastic Gradient Descent，随机梯度下降)

$$ \begin{cases} W_{t+1}=W_{t}-\eta_{t} g_{t} \\ g_{t} = \Delta J_{i_{s}}(W_{t}) \end{cases} $$
其中$W_t$表示t时刻模型参数，$g_t$表示第t次迭代的梯度，$\eta_t$表示学习率，一般取值0.001。
**SGD(随机梯度下降)**：对于每一个样本引入一些随机性和噪声，然后利用梯度下降法进行训练。
SGD优点：

梯度计算快，引入噪声增加鲁棒性，并且便于逃离鞍点，实验证明只要噪声不是特别大，SGD都能很好地收敛。
应用大型数据集，比标准的梯度下降算法快速很多。

SGD缺点：

SGD引入噪声，可能使得权值更新的方向不一定正确。
SGD难以逃离局部最优解。

在TensorFlow2.0中给我们提供了SGD的类。

import tensorflow.keras as keras


optimizer = keras.optimizers.SGD(learning_rate=0.001, momentum=0.0, nesterov=False, name='SGD')

Momentum(使用动量的随机梯度下降)

$$ \begin{cases} W_{t+1}=W_{t} - v_{t} \\ v_{t} = \alpha v_{t-1} + \eta \Delta J(W_{t}) \end{cases} $$
其中$W_t$表示t时刻模型参数，$v_t$表示当前积攒的速度，$\alpha$表示动力大小，一般取值0.9，$\Delta J(W_t)$表示第t次迭代的梯度，$\eta_t$表示学习率，一般取值0.001。
**Momentum(使用动量的随机梯度下降)**：引入一个积攒的梯度信息动量进行加速随机梯度下降法的训练过程。
Momentum优点：

加速SGD的收敛。
引入动量的思想，可能会冲破局部最小值的影响。

Momentum缺点：

依赖动量可能会使下降速度越来越大，使得冲上另一个山坡。

在TensorFlow2.0中SGD类属性引入了动量因子，因此调用SGD即可。

import tensorflow.keras as keras


optimizer = keras.optimizers.SGD(learning_rate=0.001, momentum=0.9, nesterov=False, name='Momentum')

NAG(Nesterov accelerated gradient，牛顿加速梯度)

$$ \begin{cases} W_{t+1}=W_{t} - v_{t} \\ v_{t} = \alpha v_{t-1} + \eta \Delta J(W_{t} - \alpha v_{t - 1}) \end{cases} $$
其中$W_t$表示t时刻模型参数，$v_t$表示当前积攒的速度，$\alpha$表示动力大小，一般取值0.9，$\Delta J(W_t)$表示第t次迭代的梯度，$\eta_t$表示学习率，一般取值0.001。
**NAG(牛顿加速梯度)**：是Momentum的变种，引入了一个校正因子，使得Momentum不会盲目听从动量指示，能提前知道自己下一步去哪里，并且预防下坡过头而冲上另一个山坡。
NAG优点：

较好的解决了Momentum中存在的速度过快的情况。

NAG缺点：

引入了修正因子，根据本次的权重和上次的速度，得到可能的下一次权重，然后计算该权重的梯度，因此需要再进行一次前向传播和后向传播，速度大大降低。

在TensorFlow2.0中SGD类属性引入了nesterov动量，因此调用SGD即可。

import tensorflow.keras as keras


optimizer = keras.optimizers.SGD(learning_rate=0.001, momentum=0.9, nesterov=True, name='NAG')

AdaGrad

$$W_{t+1}=W_t - \frac{\eta_0}{\sqrt{\sum_{t’=1}^t g_{t’,i}^2} + \epsilon} \cdot g_{t, i}$$

其中$W_t$表示t时刻模型参数，$g_{t, i}$表示第t次迭代的梯度，$\epsilon$避免分母为0，一般取值1e-7，$\eta_t$表示初始学习率，一般取值0.001。
AdaGrad：独立适应所有参数的学习率，缩放每个参数反比于其梯度历史总和的平方根，具有大梯度的参数有较大的学习率，小梯度的参数有较小的学习率
AdaGrad优点：

对于出现较多的特征或类别，给予较小的学习率，对于出现较少的特征或类别，给予较大的学习率，适合于稀疏数据或者分布不平衡的数据集。
不需要人为调节学习率，它可以完成自动调节。

AdaGrad缺点：

随着迭代次数的增加，学习率会越来越小，最终趋近于0。

在TensorFlow2.0中给我们提供了AdaGrad的类

import tensorflow.keras as keras


optimizer = keras.optimizers.Adagrad(learning_rate=0.001, epsilon=1e-7)

RMSProp

$$ \begin{cases} W_{t+1}=W_{t} - \frac{\eta_0}{\sqrt{E[g^2]_t} + \epsilon} \cdot g_t \ E[g^2]t = \alpha E[g^2]{t - 1} + (1 - \alpha)g_t^2 \end{cases} $$
其中$W_t$表示t时刻模型参数，$g_t$表示第t次迭代的梯度，$\epsilon$避免分母为0，一般取值1e-7，$\eta_t$表示全局学习率，一般取值0.001，$\alpha$表示动力大小，一般取值0.9，$E[g^2]_t$表示前t次的梯度平方的均值。
RMSProp：是对AdaGrad的改进，修改了AdaGrad的梯度累加变为加权平均。
RMSProp优点：

由于使用加权平均，可以避免AdaGrad中学习率越来越低的问题。

在TensorFlow2.0中给我们提供了RMSProp的类

import tensorflow.keras as keras


optimizer = keras.optimizers.RMSProp(learning_rate=0.001, rho=0.9, epsilon=1e-7)

AdaDelta

$$ \begin{cases} W_{t+1}=W_t + \Delta W_t \ \Delta W_t = -\frac{\sqrt{\sum_{i=1}^{t-1}{\Delta W_i}}}{\sqrt{E[g^2]_t} + \epsilon} \cdot g_t \ E[g^2]t = \alpha E[g^2]{t - 1} + (1 - \alpha)g_t^2 \end{cases} $$
其中$W_t$表示t时刻模型参数，$g_t$表示第t次迭代的梯度，$\epsilon$避免分母为0，一般取值1e-7，$\alpha$表示动力大小，一般取值0.95，$E[g^2]_t$表示前t次的梯度平方的均值。
AdaDelta：和RMSProp公式基本相同，在相同的时间被独立的提出。
AdaDelta优点：

不需要设置全局学习率。

AdaDelta缺点：

在模型训练的后期，模型会反复地在局部最小值附近抖动。

在TensorFlow2.0中给我们提供了AdaDelta的类

import tensorflow.keras as keras


# 其中的learning_rate匹配论文中的精确形式，使用1.0，等效为实现与学习率无关
optimizer = tf.keras.optimizers.AdaDelta(learning_rate=1.0, rho=0.95, epsilon=1e-7)

Adam

$$ \begin{cases} W_{t+1}=W_t - \frac{\eta}{\sqrt{\hat{v_t}} + \epsilon} \hat{m_t} \ \hat{m_t} = \frac{m_t}{1-\beta_1^t}，\hat{v_t} = \frac{v_t}{1-\beta_2^t} \ v_t = \beta_2 v_{t-1} + (1-\beta_2)g_t^2 \ m_t = \beta_1 m_{t-1} + (1-\beta_1)g_t \end{cases} $$
其中$m_t，v_t$分别表示一阶动量和二阶动量，$\beta_1，\beta_2$分别表示动力大小，一般取值0.9和0.999，$\hat{m_t}，\hat{v_t}$分别为各自的修正值，$W_t$表示第t次迭代模型参数，$g_t$表示第t次迭代的梯度，$\epsilon$避免分母为0，一般取值1e-7，$\eta_t$表示全局学习率，一般取值0.001。
Adam：通过计算梯度的一阶矩估计和二阶矩估计而为不同的参数设计独立的自适应学习率，同时获得AdaGrad和RMSProp的优点，在很多情况是算默认工作性能比较优秀的优化器。
Adam优点：

充分利用了梯度的二阶矩。
适用于不稳定的目标函数，鲁棒性强。
适用于大规模的数据和参数的场景。

在TensorFlow2.0中给我们提供了Adam的类

import tensorflow.keras as keras


optimizer = tf.keras.optimizers.Adam(learning_rate=0.001, beta1=0.9, beta_2=0.999, epsilon=1e-7)

优化器的比较

在下降速度上：自适应学习优化器(AdaGrad，RMSProp，AdaDelta，Adam)和动量优化器(Momentum，NAG)明显快于SGD。

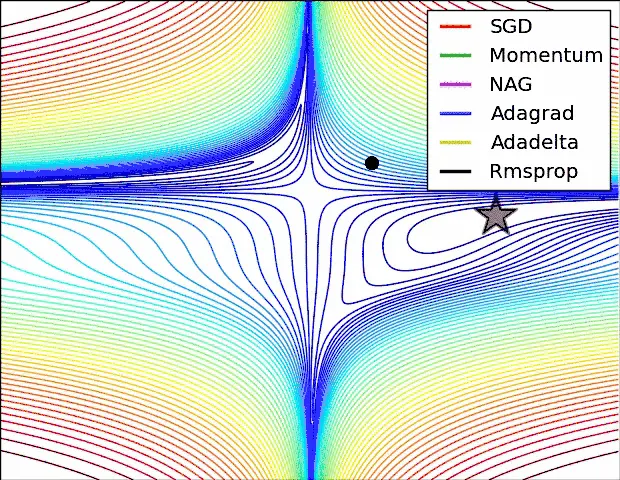
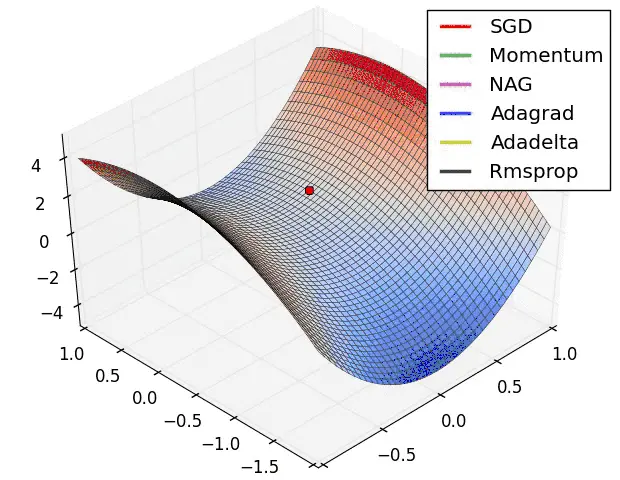
optimizer

在下降轨迹上：SGD和自适应学习优化器大致相同，动量优化器因为动量原因，可能会越过最低点，导致多走一段距离。

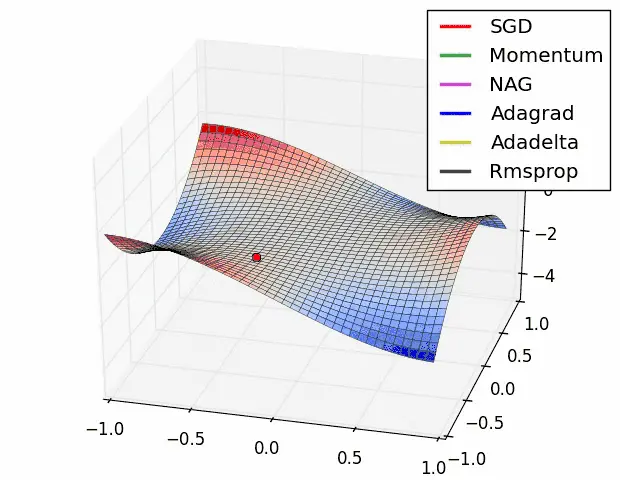
optimizer

在运行效果上：自适应学习优化器和动量优化器基本不会停留在鞍点，而SGD可能会停留在鞍点。

optimizer

小结

在选择优化器的时候，往往首先考虑Adam优化器，如果Adam优化器的效果不好，可以尝试RMSProp，然后再考虑其他的优化器。但是在实际的工程应用中，不同的优化器适合不同的场景，不能说明在任何情况下Adam都比其他的优化器更加优秀，选择哪种优化器应该结合具体的问题进行分析，而且要小伙伴们要记住模型效果不好可能是多方面原因造成的，可能是模型结构太小，或者参数设置不合理，或者损失函数设计偏差等等，不能盲目地更换优化器来提升性能。