Learning Rate

背景介绍

Learning Rate(学习率):深度学习中有一个重要的参数为学习率，小伙伴们应该都知道，这是设置优化器时的一个必要参数，学习率指导我们在梯度下降的过程中，如何去使用损失函数的梯度调整网络的权重。因此对网络的影响是非常重要的。今天给小伙伴们盘点一下常用的学习率黑科技。

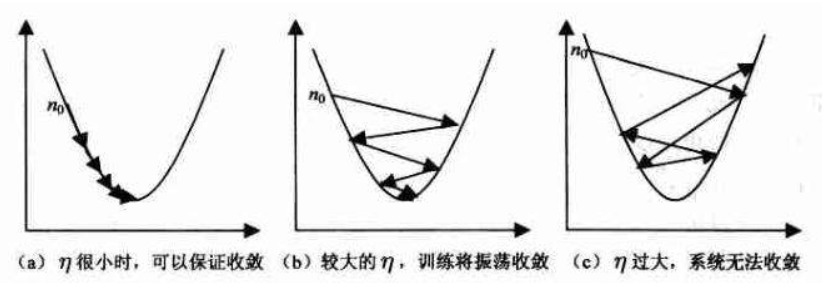
learning_rate

学习率特点

大学习率优点：

能够加速学习速率，更快的使Loss变小，且容易跳出局部最优值。
大学习率缺点：
可能导致模型在极小值震动，使模型不精确。

小学习率优点：

帮助模型收敛，有助于模型细化，提高模型精度。
小学习率缺点：
收敛缓慢，可能被困在某个局部最小值附近。

因此在深度学习工程中，既要使用大学习率加速收敛，跳出局部最优，也要使用小学习率，提高模型精度。所以我们需要在训练过程中修改学习率的大小。

fixed(固定值)

$$ lr = \eta $$
其中$ \eta $为初始学习率
在TensorFlow2.0中已经给我们提供了自定义学习率的类LearningRateScheduler。

def scheduler(epoch):
    lr = base_lr 
    print('\nBatch %d: setting learning rate to %s.' % (epoch + 1, lr))
    return lr

base_lr = 0.01
max_epoch = 100
reduce_lr = keras.callbacks.LearningRateScheduler(scheduler)
model.fit(db, epochs=max_epoch, callbacks=[reduce_lr], validation_data=db_test)

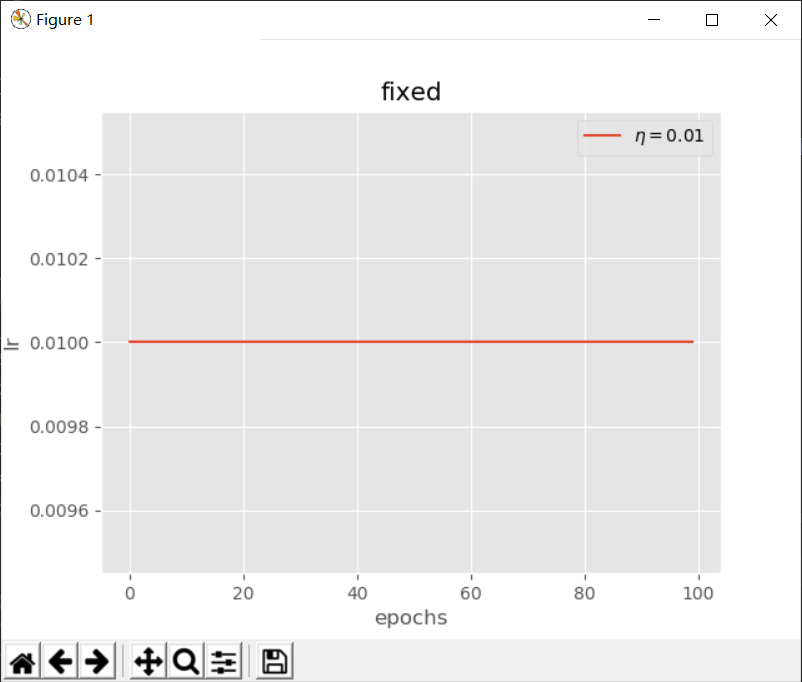
fixed

step(阶梯下降)

$$ lr = \eta * \gamma^{\left\lfloor {\frac{epoch}{step}} \right\rfloor} $$
其中$ \eta $为初始学习率，$ epoch $为当前迭代次数，$ \gamma $为下降比例，$ step $为下降周期
在TensorFlow2.0中已经给我们提供了自定义学习率的类LearningRateScheduler。

import tensorflow as tf
import tensorflow.keras as keras

def scheduler(epoch):
    lr = base_lr * gamma ** (epoch // step_size)
    print('\nBatch %d: setting learning rate to %s.' % (epoch + 1, lr))
    return lr

base_lr = 0.01
step_size = 10
gamma = 0.1
max_epoch = 100
reduce_lr = keras.callbacks.LearningRateScheduler(scheduler)
model.fit(db, epochs=max_epoch, callbacks=[reduce_lr], validation_data=db_test)

step

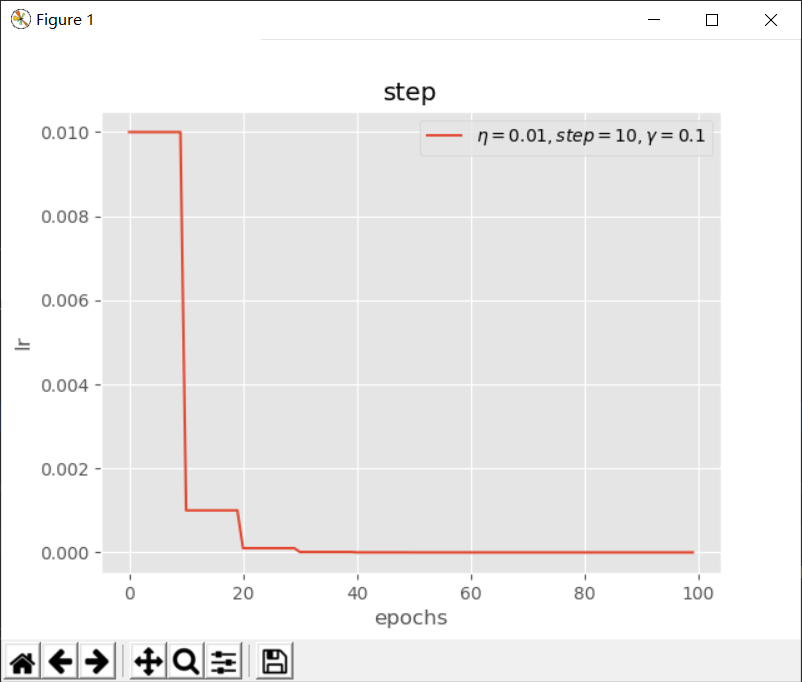
exp(指数下降)

$$ lr = \eta * (\gamma^{epoch})$$
其中$ \eta $为初始学习率，$ epoch $为当前迭代次数，$ \gamma $为指数下降底数
在TensorFlow2.0中已经给我们提供了自定义学习率的类LearningRateScheduler。

def scheduler(epoch):
    lr = base_lr * gamma ** epoch
    print('\nBatch %d: setting learning rate to %s.' % (epoch + 1, lr))
    return lr

base_lr = 0.01
gamma = 0.9
max_epoch = 100
reduce_lr = keras.callbacks.LearningRateScheduler(scheduler)
model.fit(db, epochs=max_epoch, callbacks=[reduce_lr], validation_data=db_test)

exp

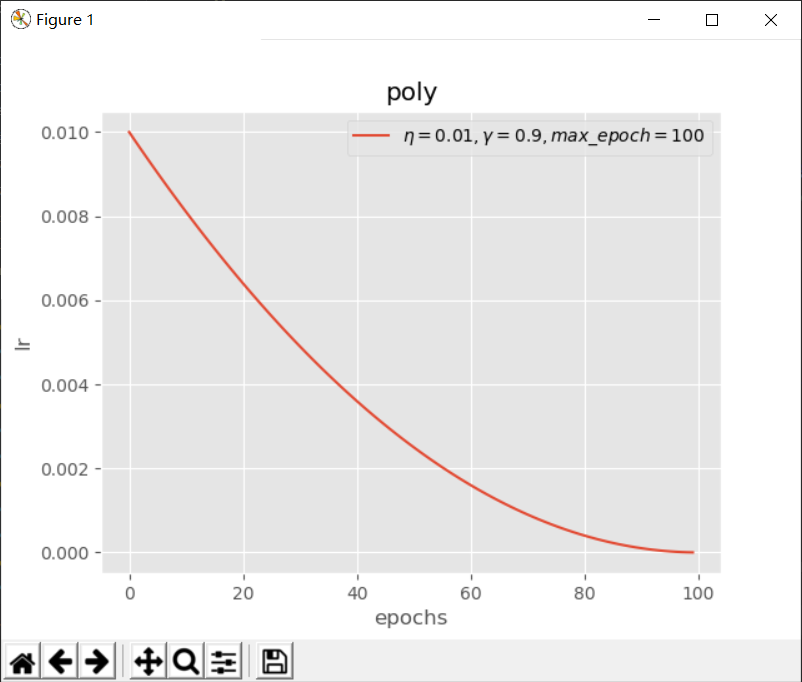
poly(多项式下降)

$$ lr = \eta * (1 - \frac{epoch}{max_epoch})^\gamma$$
其中$ \eta $为初始学习率，$ epoch $为当前迭代次数，$ max_epoch $为最大迭代次数，$ \gamma $为多项式的幂
在TensorFlow2.0中已经给我们提供了自定义学习率的类LearningRateScheduler。

def scheduler(epoch):
    lr = base_lr * (1 - epoch / max_epoch) ** gamma
    print('\nBatch %d: setting learning rate to %s.' % (epoch + 1, lr))
    return lr

base_lr = 0.01
gamma = 2
max_epoch = 100
reduce_lr = keras.callbacks.LearningRateScheduler(scheduler)
model.fit(db, epochs=max_epoch, callbacks=[reduce_lr], validation_data=db_test)

poly

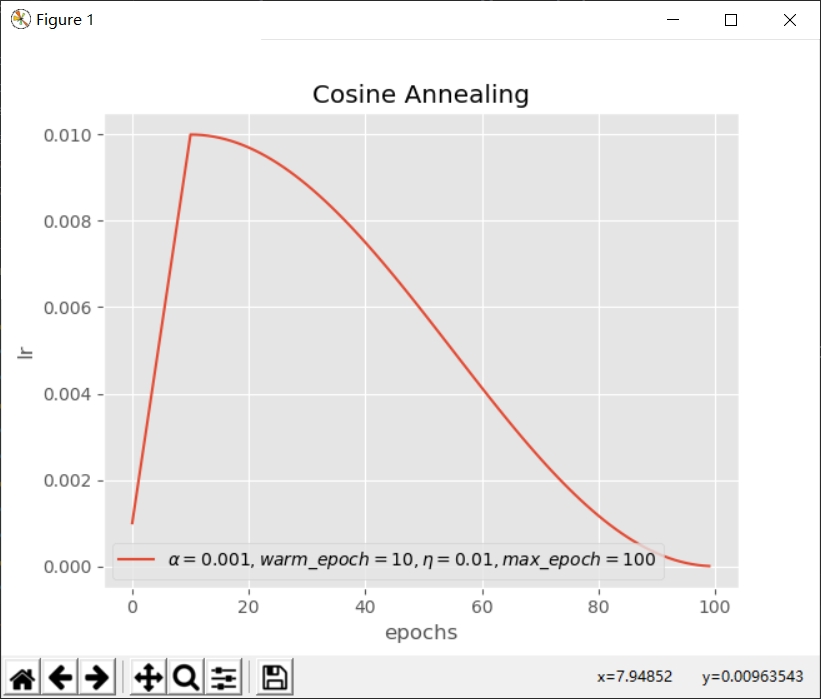
Cosine Annealing(余弦退火)

$$ lr = \begin{cases} epoch \times \frac{ \eta - \alpha }{ warm_epoch } + \alpha & epoch \le warm_epoch \ 0.5 \times \eta \times (1 + \cos{(\pi * \frac{epoch - warm_epoch}{max_epoch - warm_epoch})})& epoch > warm_epoch \end{cases}$$
其中$ \alpha $为初始学习率，$ \eta $为最高学习率，$ epoch $为当前迭代次数，$ max\_epoch $为最大迭代次数，$ warm\_epoch $为开始退火的迭代次数
在TensorFlow2.0中已经给我们提供了自定义学习率的类LearningRateScheduler。

def scheduler(epoch):
    lr = (base_lr - begin_lr) / warm_epoch * epoch + begin_lr if epoch <= warm_epoch else 0.5 * base_lr * (1 + np.cos(np.pi * (epoch - warm_epoch) / (max_epoch - warm_epoch)))
    print('\nBatch %d: setting learning rate to %s.' % (epoch + 1, lr))
    return lr

base_lr = 0.01
begin_lr = 0.001
max_epoch = 100
warm_epoch = 10
reduce_lr = keras.callbacks.LearningRateScheduler(scheduler)
model.fit(db, epochs=max_epoch, callbacks=[reduce_lr], validation_data=db_test)

cosine

ReduceLROnPlateau

Plateau意思为高原，从其英文表达中可以清晰的看出，当要监视的值出现平坦时，学习率会下降。
在TensorFlow2.0中已经给我们提供了ReduceLROnPlateau类，其常用参数有

monitor：要监视的值，默认为val_loss。
factor：学习率下降因子，new_lr = lr x factor。
patience：耐心周期，如果在patience周期内没有改善，则降低学习率。
min_lr：设置最低学习率，防止学习率过低。

因为ReduceLROnPlateau可以实现自适应的学习率变化，而且不需要去自定义学习率下降方法，所以大部分情况下使用ReduceLROnPlateau即可完成训练任务。

base_lr = 0.01
begin_lr = 0.001
max_epoch = 100
warm_epoch = 10
reduce_lr = tf.keras.callbacks.ReduceLROnPlateau(monitor='val_loss', factor=0.1, patience=10, min_lr=0)
model.fit(db, epochs=max_epoch, callbacks=[reduce_lr], validation_data=db_test)

model.optimizer.lr.assign

在Model类对象中，有optimizer.lr属性，其保存着学习率的值，使用assign方法可以设置学习率。在自定义训练过程中，常常使用这种方法进行学习率动态修改。

1	model.optimizer.lr.assign(model.optimizer.lr / 2)

小结

小伙伴们观察几个常见学习率函数后发现，都是呈现一个递减的函数，递减是因为模型刚开始训练，需要加速收敛，而且容易落入局部最小值，因此需要较大的学习率，随着学习的推进，我们需要对模型进行细化，使其精度提高，因此需要较小的学习率。在这个博客里列举的是一些常用的学习率下降函数，大家可以根据自己的实际问题进行调整，只要是满足递减条件，都可以用来尝试。