Metrics黑科技

发表于 | 分类于 ， | | 本文总阅读数 次
| 字数统计: 3.4k | 阅读时长 ≈ 12
Metrics

Metrics

背景介绍

  Metrics(评价指标):评价指标是检验神经网络模型好坏的评定依据，也是我们要达到的最终目标，指标越好则我们的任务完成的越好。有时我们需要根据评价指标修改我们的网络模型，参数等等，就类似于考试成绩一样，我们根据成绩检验自己薄弱的地方，然后去调整和修改，神经网络也是一样，只有建立好合适的评价指标，才能真正区分网络的优劣。今天给小伙伴们介绍深度学习中常用的评价指标。

confuse

Confusion matrix(混淆矩阵)

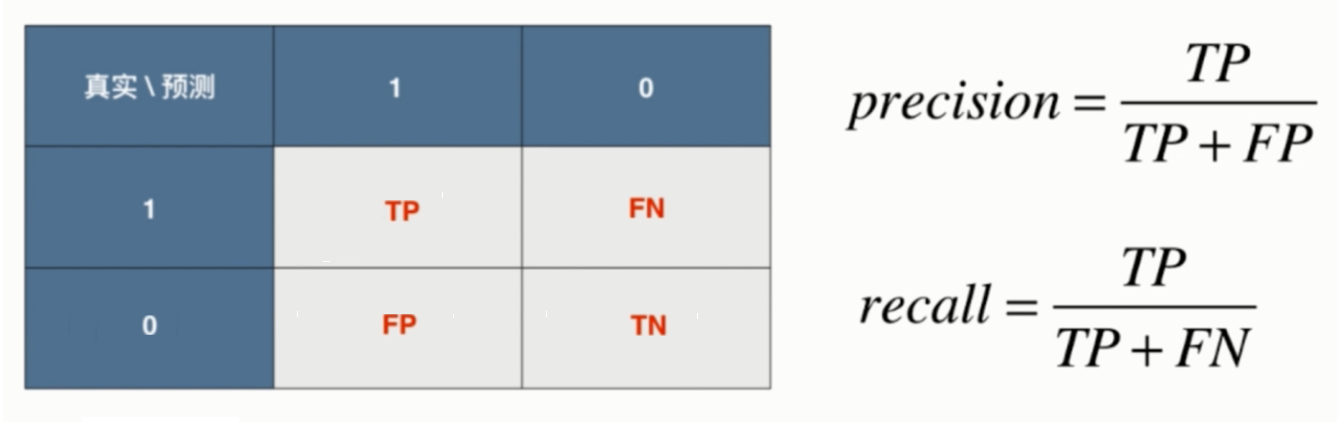
在介绍评价指标之前，首先要介绍混淆矩阵，以一个二分类问题来说，行标签代表预测值为正还是为负，列标签代表真实值为正还是为负，因此产生4中状态。

  1. TP(True Positive，真正率)：真代表预测正确，正代表预测为正样本，因此含义为将正样本预测为正样本的个数。
  2. TN(True Negative，真负率)：真代表预测正确，负代表预测为负样本，因此含义为将负样本预测为负样本的个数。
  3. FP(False Positive，假正率)：假代表预测错误，正代表预测为正样本，因此含义为将负样本预测为正样本的个数。
  4. FN(False Negative，假负率)：假代表预测错误，负代表预测为负样本，因此含义为将正样本预测为负样本的个数。

混淆矩阵是将所有可能的状态列举出来，然后通过表格可以计算出相应的评价指标，对于样本不平衡问题非常有效。

Accuracy(准确率)

$$ acc = \frac{TP + TN}{TP + TN + FP + FN} $$
Accuracy(准确率)：指正确预测的数量与总数的比值，准确率越高则代表预测的越准确。在TensorFlow2.0中已经给我们提供了计算Accuracy的评价函数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import tensorflow as tf
import tensorflow.keras as keras

# 计算准确率，必须完全相等才算准确
metrics = keras.metrics.Accuracy()

# 计算二分类准确率，大于threshold即算为准确
metrics = keras.metrics.BinaryAccuracy(threshold=0.5)

# 计算多分类准确率
metrics = keras.metrics.CategoricalAccuracy()

# 计算TopK多分类准确率，k默认为5
metrics = keras.metrics.TopKCategoricalAccuracy(k=5)

Precision(精确度)

$$ precision = \frac{TP}{TP + FP} $$
Precision(精确度)：又称为查准率，指正样本预测为正的数量与所有样本预测为正的数量的比值，精确度越高，代表对预测为正的样本中，正样本的比例越高。当负样本判断错误的成本非常高，正样本判断错误的成本非常低的时候，我们选择较高的精确度，保证预测为正的样本中，负样本尽可能少，减少负样本判断错误的成本。在TensorFlow2.0中已经给我们提供了计算Precision的评价函数。

1
2
3
4
5
import tensorflow as tf
import tensorflow.keras as keras

# 默认选择阈值为0.5
metrics = keras.metrics.Precision(thresholds=None)

Recall(召回率)

$$ recall = \frac{TP}{TP + FN} $$
Recall(召回率)：又称为敏感度(Sensitivity)，查全率，指正样本预测为正的数量与所有正样本的数量的比值，召回率越高，代表所有正样本中，预测为正的样本的比例越高。当正样本判断错误的成本非常高，负样本判断错误的成本非常低的时候，我们选择较高的召回率，保证正样本尽可能被判断正确，减少正样本判断错误的成本。在TensorFlow2.0中已经给我们提供了计算Recall的评价函数。

1
2
3
4
5
import tensorflow as tf
import tensorflow.keras as keras

# 默认选择阈值为0.5
metrics = keras.metrics.Recall(thresholds=None)

F1-score

$$ F1-score = \frac{2}{\frac{1}{precision} + \frac{1}{recall}} = \frac{2 \times precision \times recall}{precision + recall} $$
F1-score：精确度和召回率的分子是相同的，分母有差异，两者是此消彼长的，究竟如何选择两者之间的权重，需要结合具体问题具体分析，判断是正样本判断错误的成本高还是负样本判断错误的成本高。为了兼顾精确度和召回率，引入了两者的调和平均数F1-score作为指标。在TensorFlow2.0中没有计算F1-score的评价函数，需要自己定义计算方法。

  1. 继承keras.metrics.Metric类
  2. 在__init__(): 中变量要通过下面这种方式创建self.var = self.add_weight(name=name, initializer=’zeros’)
  3. 在update_state():中变量要通过下面这种方式更新self.var.assign_add()
  4. 在result()中: 返回变量

Specificity(特异度)

$$ specificity = \frac{TN}{FP + TN} $$
Specificity(特异度)：指负样本预测为负的数量与所有负样本的数量的比值，特异度越高，代表所有负样本中，预测为负的样本的比例越高。在TensorFlow2.0中没有计算Specificity的评价函数，需要自己定义计算方法，步骤如下。

  1. 继承keras.metrics.Metric类
  2. 在__init__(): 中变量要通过下面这种方式创建self.var = self.add_weight(name=name, initializer=’zeros’)
  3. 在update_state():中变量要通过下面这种方式更新self.var.assign_add()
  4. 在result()中: 返回变量

FPR(假正率)

$$ FPR = 1 - specificity = \frac{FP}{FP + TN} $$
FPR(假正率)：指负样本预测为正的数量与所有负样本的数量的比值，假正率越低，代表所有负样本中，预测为正样本的比例越低。在TensorFlow2.0中已经给我们提供了计算假正个数的评价函数，是将数据最后一个维度计算之后，对所有结果求和。

1
2
3
4
5
import tensorflow as tf
import tensorflow.keras as keras

# 默认选择阈值为0.5，注意计算的是个数，而不是比例
metrics = keras.metrics.FalsePositives(thresholds=None)

ROC Curve(Receiver Operating Characteristic，受试者操作特性曲线)

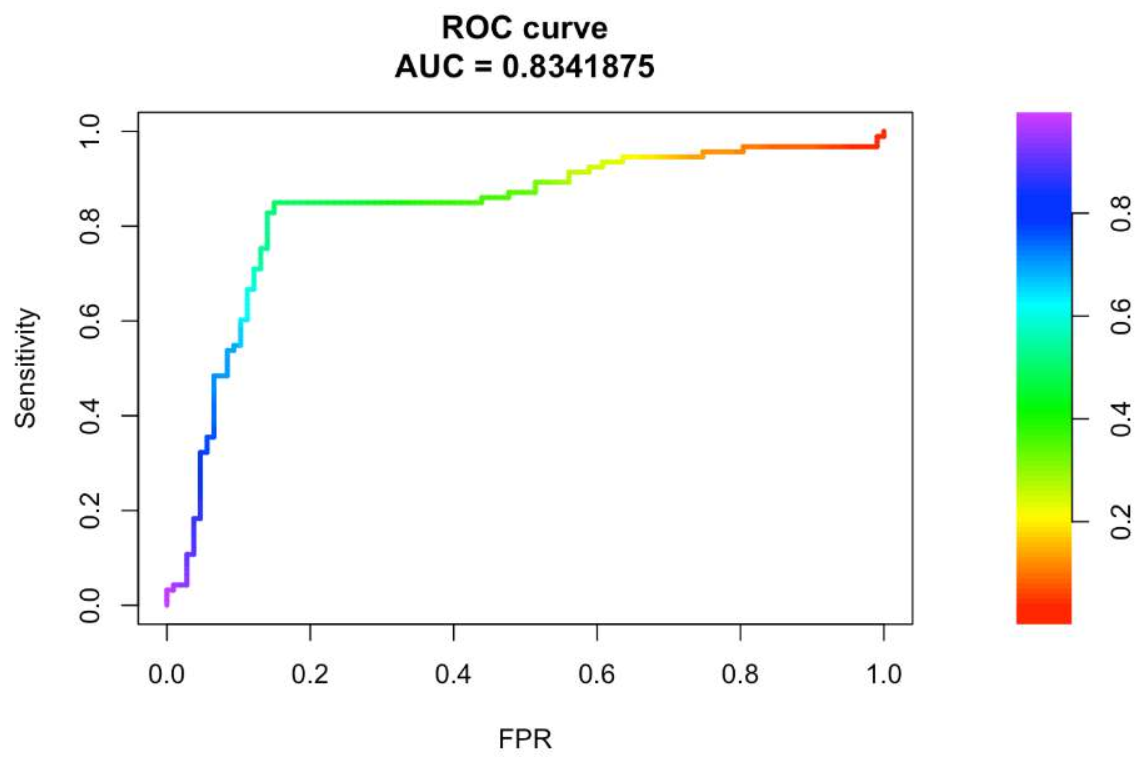
ROC Curve：是一条以不同阈值下的FPR(假正率)为横坐标，不同阈值下的Recall(召回率)为纵坐标的曲线。
ROC曲线绘制步骤：

  1. 从高到低，依次将每个测试样本属于正样本的概率值从大到小排序。
  2. 根据排序，从高到低依次将概率值作为阈值，当概率大于等于这个阈值时，预测为正样本，否则预测为负样本。
  3. 根据步骤2得到的结果计算FPR和Recall，遍历所有样本，得到一组(FPR, Recall)，并和阈值取值为0和1下的(FPR, Recall)结合在图像上绘制出来，就可以得到ROC曲线。

ROC曲线特性：

  1. 当测试集中的正负样本的分布变化的时候，ROC曲线能够保持不变，这是ROC曲线的最大优点，但是如果正负样本的成本差距较大，则很难从ROC曲线中看出结论。
  2. ROC曲线越接近左上角代表模型的效果越好。
    roc

AUC(Area Under Curve，ROC曲线下的面积)

AUC：定义为ROC曲线下的面积，值域为[0, 1]，该值越大，代表ROC曲线越接近左上角，说明模型效果越好。在TensorFlow2.0中已经给我们提供了计算AUC的评价函数。

1
2
3
4
5
import tensorflow as tf
import tensorflow.keras as keras

# 默认选择计算阈值的个数为200个
metrics = keras.metrics.AUC(num_thresholds=200)

PR Curve(Precision Recall Curve，查准率查全率曲线)

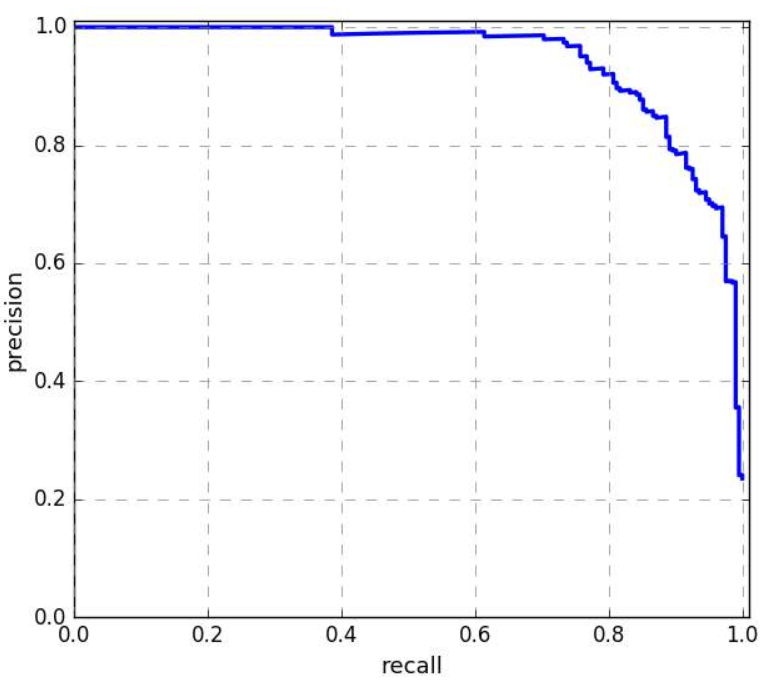
PR Curve：是一条以不同阈值下的Recall(查全率)为横坐标，不同阈值下的Precision(查准率)为纵坐标的曲线。
PR曲线绘制步骤：

  1. 从高到低，依次将每个测试样本属于正样本的概率值从大到小排序。
  2. 根据排序，从高到低依次将概率值作为阈值，当概率大于等于这个阈值时，预测为正样本，否则预测为负样本。
  3. 根据步骤2得到的结果计算Recall和Precision，遍历所有样本，得到一组(Recall, Precision)，并和阈值取值为0和1下的(Recall, Precision)结合在图像上绘制出来，就可以得到PR曲线。

PR曲线特性：

  1. PR曲线的两个指标都聚焦于正样本，因此在类别不平衡问题中主要关心正样本，在正负样本的成本差距较大情况下，PR曲线优于ROC曲线。
  2. PR曲线越接近右上角代表模型的效果越好。
    pr

AP(Average Precision，平均精度)和mAP(mean Average Precision)

AP(平均精度)：定义为PR曲线下的面积，值域为[0, 1]，该值越大，代表PR曲线越接近右上角，说明模型效果越好。
mAP：对每个类的AP求平均，值域为[0, 1]，该值越大，说明模型效果越好，因为目标检测算法中存在正负样本不平衡的问题，因此mAP是目标检测算法中最重要的指标之一。在TensorFlow2.0中没有计算AP的评价函数，需要自己定义计算方法，步骤如下。

  1. 继承keras.metrics.Metric类
  2. 在__init__(): 中变量要通过下面这种方式创建self.var = self.add_weight(name=name, initializer=’zeros’)
  3. 在update_state():中变量要通过下面这种方式更新self.var.assign_add()
  4. 在result()中: 返回变量

IOU(Intersection Over Union，交并比)

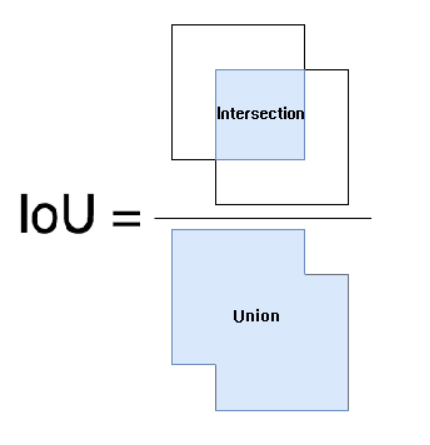
IOU(交并比)：可以理解为算法的结果与标记结果的重合程度，算法的结果与真实物体进行交运算的结果除以进行并运算的结果。用于评估语义分割算法性能的指标是平均IOU，通过下图可以直观的看出IOU的计算方法，IOU的值越大，算法的效果越好。在TensorFlow2.0中没有计算IOU的评价函数，需要自己定义计算方法，步骤如下。

  1. 继承keras.metrics.Metric类
  2. 在__init__(): 中变量要通过下面这种方式创建self.var = self.add_weight(name=name, initializer=’zeros’)
  3. 在update_state():中变量要通过下面这种方式更新self.var.assign_add()
  4. 在result()中: 返回变量
    IOU

MSE(Mean Squared Error，均方误差)

$$ MSE = \frac{1}{N} \sum_{i=1}^{N}{(y^{(i)} - f(x^{(i)}))^2} $$
MSE(均方误差)：指预测结果与真实值之差平方的期望值，其中平方误差是估计值和实际值之差的平方，也称为(L2 Loss)，MSE可以评价数据的变化程度，MSE的值越小，说明预测模型描述实验数据具有更好的精确度。在TensorFlow2.0中已经给我们提供了计算MSE的评价函数，是将数据最后一个维度计算之后，对所有结果求平均值。

1
2
3
4
import tensorflow as tf
import tensorflow.keras as keras

metrics = keras.metrics.MeanSquaredError()

MAE(Mean Absolute Error，平均绝对误差)

$$ MAE = \frac{1}{N} \sum_{i=1}^{N}{|y^{(i)} - f(x^{(i)})|} $$
MAE(平均绝对误差)：指预测结果与真实值绝对误差的平均值，其中绝对误差是估计值和实际值之间的距离，也称为(L1 Loss)，MAE能更好地反映预测值误差的实际情况。在TensorFlow2.0中已经给我们提供了计算MAE的评价函数，是将数据最后一个维度计算之后，对所有结果求平均值。

1
2
3
4
import tensorflow as tf
import tensorflow.keras as keras

metrics = keras.metrics.MeanAbsoluteError()

Binary Cross Entropy(二分类交叉熵)

$$ Binary \ Cross \ Entropy = -\frac{1}{N} \sum_{i=1}^{N}{(y^{(i)} \cdot \ln{(f(x^{(i)})}) + (1 - y^{(i)}) \cdot (1 - \ln{(f(x^{(i)})}))} $$
Binary Cross Entropy：用来评估当前训练得到的概率分布与真实分布的差异情况，它刻画的是实际概率与期望概率的距离，也就是交叉熵的值越小，两个概率分布就越接近。在二分类中，每个数据独立计算交叉熵，和同一维度其他数据无关，允许多个1同时出现，经常配合sigmoid激活函数使用。在TensorFlow2.0中已经给我们提供了计算Binary Cross Entropy的评价函数，是将每一个数据单独计算之后，对所有数据求平均值。

1
2
3
4
import tensorflow as tf
import tensorflow.keras as keras

metrics = keras.metrics.BinaryCrossentropy()

Categorical Cross Entropy(多分类交叉熵)

$$ Categorical \ Cross \ Entropy = -\frac{1}{N} \sum_{i=1}^{N}{(y^{(i)} \cdot \ln{(f(x^{(i)})))}} $$
Categorical Cross Entropy：用来评估当前训练得到的概率分布与真实分布的差异情况，它刻画的是实际概率与期望概率的距离，也就是交叉熵的值越小，两个概率分布就越接近。在多分类中，在某个维度上计算交叉熵，在该维度上其他数据一般只有一个1出现，其他全为0，经常配合Softmax激活函数使用。在TensorFlow2.0中已经给我们提供了计算Categorical Cross Entropy的评价函数，是将数据最后一个维度计算之后，对所有结果求平均值。

1
2
3
4
import tensorflow as tf
import tensorflow.keras as keras

metrics = keras.metrics.BinaryCrossentropy()

小结

  评价函数和损失函数类似，评价函数在一定程度上可以和损失函数相互转化，如MSE，MAE，交叉熵既可以作为评价函数，又可以作为损失函数。在选择评价函数时，我们首先要判断任务类型，是分类任务还是回归任务。分类任务可以考虑Accuracy评价函数，回归任务可以考虑MSE或者MAE评价函数。也可以根据正负样本的损失比例，来给予Precision和Recall一定的权重。在实际的工程应用之中，往往需要自己设计一个合适的评价函数，如目标检测问题，就需要设计一个mAP评价函数，目标分割问题，就需要设计一个IOU评价函数。因此小伙伴们需要多实践，多尝试，实践出真知。

-------------本文结束感谢您的阅读-------------
0%