背景介绍
Error,Bias,Variance,Noise(误差,偏差,方差,噪声):是机器学习中的一组重要概念,小伙伴们可能也听说过这些,但是可能不清楚它们之间到底有什么练习,今天给大家捋一捋。
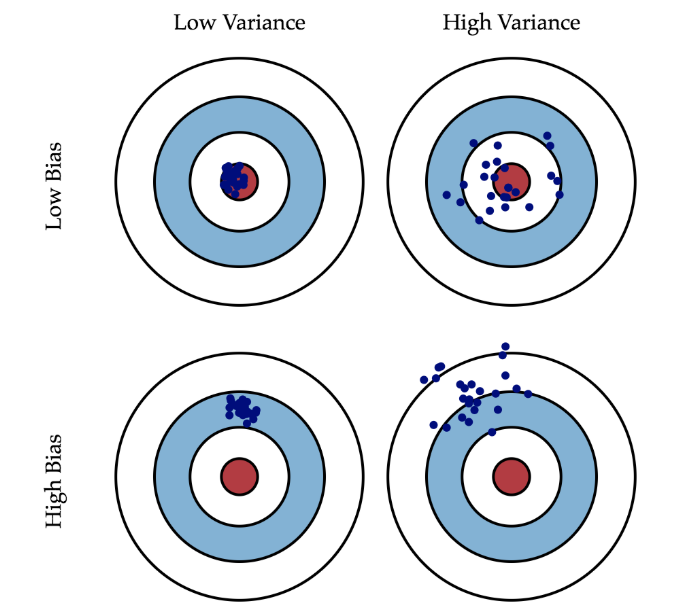
误差,偏差,方差,噪声的定义
Error(误差):把学习器的实际预测输出与样本的真是输出之间的差异称为误差,一般定义为损失函数Loss,学习的主要目的就是最小化Loss。在训练数据上得到的Loss称之为training erroe(训练误差),在新样本数据得到的Loss称之为(generalization erroe)泛化误差。显然,我们希望得到泛化误差小的学习器。
Bias(偏差):度量算法的期望预测与真实结果的偏离程度,刻画了学习算法本身的拟合能力。
Variance(方差):度量同样大小的不同训练集所导致学习性能的变化,刻画了数据扰动的影响。
Noise(噪声):表达了当前任务上,学习器所能到达的泛化误差的下界,刻画了学习本身的难度,可以理解为数据的label本身就是不准确的,因此模型无论如何学习都不可能消除。
误差,偏差,方差,噪声的关系
下面用公式具体说明它们四者之间的关系,首先定义一些符号,这里参考了周志华老师的《机器学习》,也许叫它西瓜书可能更知名一些,一个一边吃西瓜一边给你侃机器学习的大牛。令测试样本为$x$,令$y_D$为$x$的标签,$y$为$x$的真实标签,$f(x;D)$为训练集$D$上学得得模型$f$对$x$得预测输出。
模型得期望预测结果为,各训练集预测结果的均值,用公式表达如下式
$$ \overline{f}(x) = E[f(x;D)] $$
不同训练集上产生得训练方差为,各训练集预测结果减模型的期望预测结果的均值,用公式表达如下式
$$ var(x) = E[(f(x;D) - \overline{f}(x))^2] $$
样本中存在的噪声为,数据集中的标签$y_D$与数据$x$的真实标签$y$之间的差异,用公式表达如下式
$$ \epsilon^2 = E[(y_D - y)^2] $$
该系统的偏差为,期望输出与真实标记之间的差异,用公式表达如下式
$$ bias^2(x) = (\overline{f}(x) - y)^2 $$
假设噪声的期望为0,$E[y_D - y] = 0$
下面对期望泛化误差进行分解
$$ \begin{align} E[f;D] & = E[(f(x;D) - y_D)^2] \\ & = E[(f(x;D) - \overline{f}(x) + \overline{f}(x) - y_D)^2] \\ & = E[(f(x;D - \overline{f}(x))^2] + E[(\overline{f}(x) - y_D)^2] + 2E[(f(x;D) - \overline{f}(x))(\overline{f}(x) - y_D)] \\ & = E[(f(x;D) - \overline{f}(x))^2] + E[(\overline{f}(x) - y_D)^2] \\ & = E[(f(x;D) - \overline{f}(x))^2] + E[(\overline{f}(x) - y + y - y_D)^2] \\ & = E[(f(x;D) - \overline{f}(x))^2] + E[(\overline{f}(x) - y)^2] + E[(y - y_D)^2] + 2E[(\overline{f}(x) - y)(y - y_D)] \\ & = E[(f(x;D) - \overline{f}(x))^2] + (\overline{f}(x) - y)^2 + E[(y_D - y)^2] \\ & = var(x) + bias^2(x) + \epsilon^2 \\ \end{align}$$
因为$ \overline{f}(x) = E[f(x;D)] \Rightarrow E[(f(x;D) - \overline{f}(x))] = 0$,因此第三行的最后一项为0
因为$E[y_D - y] = 0 \Rightarrow E[(\overline{f}(x) - y)(y - y_D)] = 0 $,因此第六行的最后一项为0
所以得到了一个结论,泛化误差可以分解为方差,偏差和噪声之和。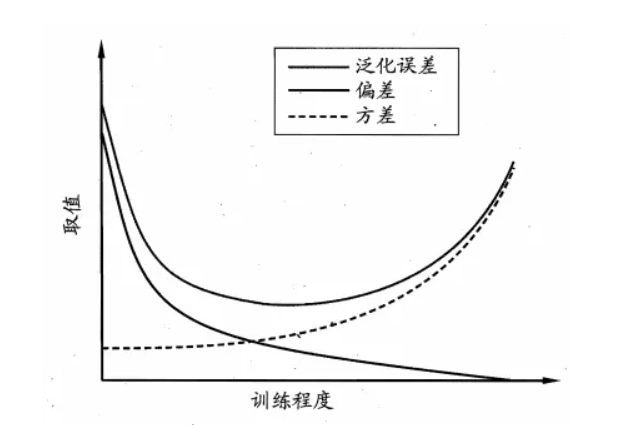
偏差和方差的相互制约
随着模型复杂度,模型迭代次数的增加,方差和偏差可能会出现此消彼长的现象,训练不足,或者模型过于简单时会出现Under-fitting(欠拟合),此时的模型误差主要来自于偏差,在训练时的表现为训练集和验证集上面的准确率都不高,说明出现了欠拟合。而训练太多,或者模型过于复杂时会出现Over-fitting(过拟合),此时的模型误差主要来自于方差,在训练时的表现为训练集上的准确率非常高,验证集上面的准确率不高,说明出现了过拟合。
如何降低泛化误差
在这里我们不讨论如何降低噪声,在我们获得数据集时,数据集本身可能就会存在噪声,因此很难进行降低。我们主要讨论如何通过降低偏差和方差来降低泛化误差。
如何降低偏差:
- 增加算法复杂度,但是要注意单纯的增加算法复杂度可能会导致方差的增加,可以结合正则项进行惩罚。
- 进行合理的特征工程,检查是否遗漏重要特征。
- 优化网络结构,因为偏差大意味着网络的拟合效果不好,因此可以更换网络层。
如何降低方差:
- 增加训练样本,样本代表性不足时方差大的首要原因,增加样本也是降低方差最简单的方法。
- **引入正则项(L1正则,L2正则,Dropout等)**。
- 特征提取,对输入的特征进行提取,特征变少方差也会减小。
- 降低模型复杂度,或者采用早停,减少迭代周期。
小结
虽然我们在使用机器学习时,很难直观的看出偏差和方差之间的关系,但是我们可能会对某些情况深有体会,如训练集的准确率达到95%,而验证集只有80%,这个情况小伙伴们都会一眼看出,过拟合了,但是过拟合背后的原因可能就不回去探究,其实过拟合就是一种方差过大的体现,这时我们就应该考虑增加训练样本,引入正则,降低模型复杂度或者采用早停等策略进行优化。还可能训练集和验证集的准确率都只达到50%,这个情况小伙伴们也应该很熟悉,欠拟合了,其实欠拟合就是一种偏差过大的体现,这时我们就应该考虑增加模型参数,优化网络结构。偏差和方差很多时候都是在理论分析时需要的,实际的工程问题,小伙伴们也可以不用去过多分析,只需要知道过拟合欠拟合该采取什么样的方法解决它,如果能够达到这样的水平,我觉得已经具备解决实际问题的能力了。