题目分析

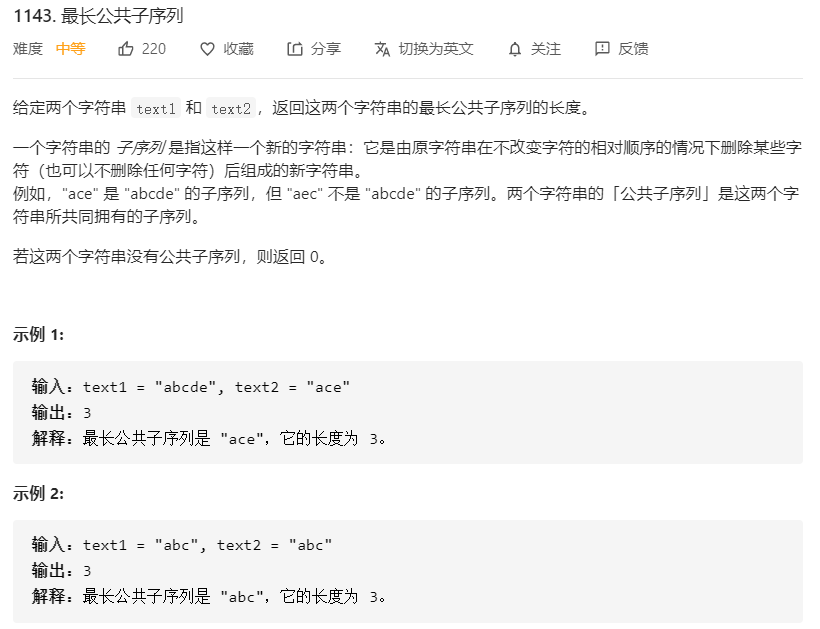
最长公共子序列(Longest Common Subsequence, LCS):是一个经典的问题，也是在某厂的笔试中遇到了这个问题，小伙伴们一定要会做呀。

DP

我们使用动态规划进行求解，dp[i][j]表示text1前i个字符和text2前j个字符的最长公共子序列，因为空序列和任何序列匹配都是0，初始状态i = 0或j = 0时，dp[i][j] = 0。可以得到状态转移方程。

$dp[i][j] = \begin{cases} dp[i - 1][j - 1] + 1 & text[i - 1] = text[j - 1] \\ max(dp[i - 1][j], dp[i][j - 1]) & text[i - 1] \ne text[j - 1] \end{cases}$
DP的时间复杂度为 $O(n^2)$ ，空间复杂度为 $O(n^2)$ 。

class Solution(object):
    def longestCommonSubsequence(self, text1, text2):
        len1, len2 = len(text1), len(text2)
        dp = [[0 for _ in range(len2 + 1)] for _ in range(len1 + 1)]
        for i in range(1, len1 + 1):
            for j in range(1, len2 + 1):
                if text1[i - 1] == text2[j - 1]:
                    dp[i][j] = dp[i - 1][j - 1] + 1
                else:
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
        return dp[-1][-1]

优化DP

动态规划一般都可以进行优化，优化的方法大多是通过空间复杂度进行优化，因为DP中保存着大量的数据，可能这些数据我们在后面的计算中并不会用到。
如此题中第i次循环，只会用到第i次循环和第i - 1次循环中的内容，之前的计算结果并不会用到，因此可以只保留第i次的结果和第i - 1次的结果，这样优化DP的时间复杂度为 $O(n^2)$ ，空间复杂度为 $O(n)$ 。

class Solution(object):
    def longestCommonSubsequence(self, text1, text2):
        if len(text1) < len(text2):
            text1, text2 = text2, text1
        len1, len2 = len(text1), len(text2)
        dp_pre, dp_cur = [0] * (len2 + 1), [0] * (len2 + 1)
        for i in range(1, len1 + 1):
            for j in range(1, len2 + 1):
                if text1[i - 1] == text2[j - 1]:
                    dp_cur[j] = dp_pre[j - 1] + 1
                else:
                    dp_cur[j] = max(dp_pre[j], dp_cur[j - 1])
            dp_cur, dp_pre = [0] * (len2 + 1), dp_cur
        return dp_pre[-1]

刷题总结

LCS问题太经典了，不需要过多介绍，干就完事了。