
题目分析
这是一个典型的数学问题,如果是一元一次方程,一元二次方程,我们可以很容易的求出根的值,这个题目是一元n次方程,因此无法获得根的表达式,这应该如何求解呢?
暴力
我们可以使用暴力法进行求解,设定一个解的区间,枚举这个区间的所有数据,因为答案要求保留两位小数,所以数字间隔$\epsilon$设为0.005即可。
- 如果某个x代入后,其结果非常接近0,那么则可以认为某个根约等于x,将x保留两位小数代替这个根。
- 如果某个x代入后不接近0,但是将$x + \epslion$代入与将x代入的结果异号,说明根处于$(x, \ x + \epslion]$,这时可以认为某个根约等于$x + \frac{\epslion}{2}$,并将其加入最后的结果之中。
这个方法无法得到全局的解,但是这种算法题不会出特别大的样例让小伙伴们计算,所以是可以通过的。
算法的**时间复杂度为$O(mn)$,空间复杂度为$O(1)$**,其中m为自己设定的范围,n为精度的倒数。
1 | import sys |
牛顿法
啊,牛顿,永远滴神。
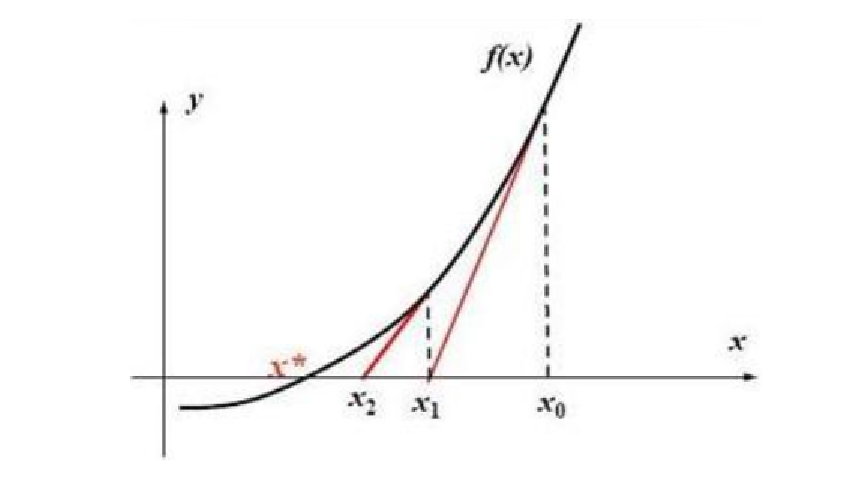
假设$f(x)$为凸函数,且处处可导,如果我们要求$f(x) = 0$的根,我们假设初始值位于$x_0$处。
那么在$x_0$处的导数为$f’(x_0)$。所以过$(x_0, f(x_0))$,斜率为$f’(x_0)$的直线会与x轴交于一点$x_1$,这个点更接近于我们要求的根。我们只要求出这个根,并且重复这个迭代过程就可以无限逼近于真实的根。
我们观察$\triangle x_1x_0f(x_0)$,可以知道
$$\frac{f(x_0)}{x0 - x1} = f’(x_0)$$
通过上面这个式子,将$x_1$用$x_0$表示为
$$x_1 = x_0 - \frac{f(x_0)}{f’(x_0)}$$
这就是牛顿法,可以通过初始点不断进行迭代逼近方程的根。
算法的**时间复杂度为$O(mn)$,空间复杂度为$O(1)$**,其中m为自己设定的范围,n为精度的倒数。
其实牛顿法做这个题目并不是很适合,牛顿法适合于求解单根问题,对于多根问题,尤其是不定根,也需要进行迭代。但是对于大多数问题来说,牛顿法可以跨度较大,如$epsilon$的值可以设置的较大,因为根在大部分情况下是散落的,但是根为0.01, 0.02, 0.03时,如果跨度较大$\epsilon = 1$,那么就可能只能得到0.01和0.03的解,在小于0时,会得到0.01的根,大于1时会得到0.03的根。如果想得到正确的结果,需要设置$\epsilon \le 0.01$。那么这种做法反而慢于暴力法。
1 | import sys |
刷题总结
这个题目并不是非常重要,也没有太多的技巧性,但是牛顿法是通过题目让小伙伴们学习的内容。