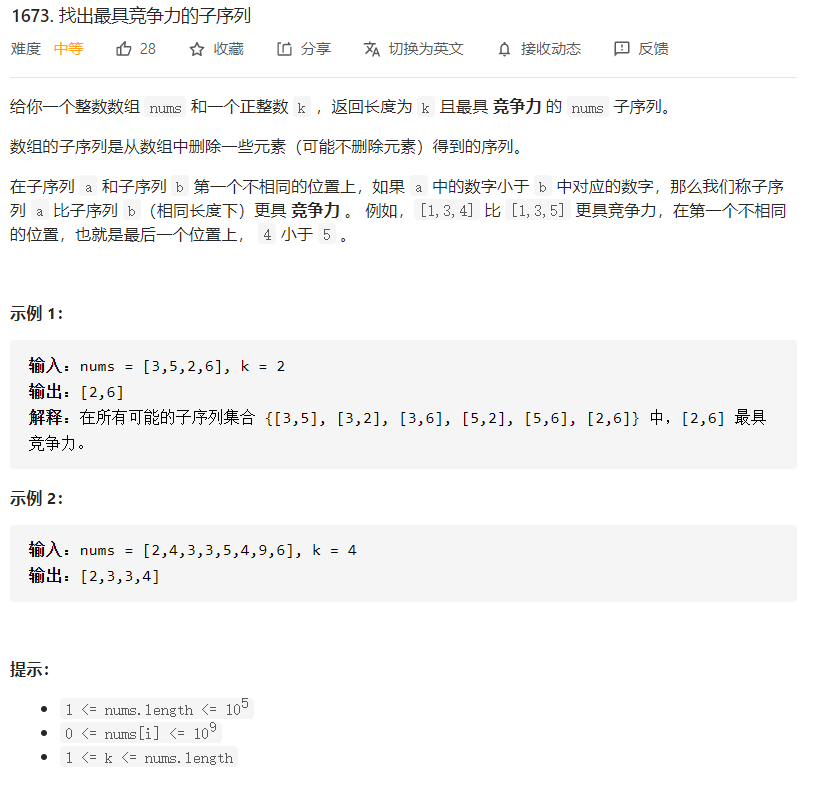
题目分析

这是第217场周赛的第二题，题目有一定的难度，希望小伙伴们能认真思考。

递归算法

这个题目可以使用递归进行求解，每次判断剩余的元素数目是否等于k，如果等于则将其全部加入结果，判断k是否等于0，如果是也可以作为递归出口。

否则我们要保留k - 1个数，找到之前所有元素的最小值加入结果序列中。这里要说明的是保留k - 1个数的目的防止后面元素不满足k个。如[3,4,2,5,1]序列，k = 2，我们先选出序列的第一个元素，我们要保留2 - 1 = 1个元素，即保留1，从3，4，2，5中选择最小的作为序列的第一个元素，如果不保留，我们选择了1，那么后面就没有序列了，因此是不正确的。

为什么要找最小值呢？这也很容易理解，1，9，9，9的竞争力也大于2，0，0，0，因此我们有一种贪心的思想，能选最小的一定先选最小的。

每次递归都需要计算从当前元素到倒数第k个元素的最小值，算法的**时间复杂度为$O(n^2)$，空间复杂度为$O(n)$**。

#include<iostream>
#include<vector>

class Solution {
public:
    vector<int> mostCompetitive(vector<int>& nums, int k) {
        vector<int> res;
        subQuestion(nums, res, 0, k);
        return res;
    }

    void subQuestion(vector<int>& nums, vector<int>& res, int left, int k) {
        if (k == 0) return;
        if (nums.size() - left == k) {
            for (int i = left; i < nums.size(); i++) res.push_back(nums[i]);
            return;
        }
        int mini = nums[left], idx = left;
        for (int i = left + 1; i < nums.size() - k + 1; i++) {
            if (nums[i] < mini) mini = nums[i], idx = i;
        }
        res.push_back(mini);
        subQuestion(nums, res, idx + 1, k - 1);
    }
};

队列优化的迭代算法

能用递归求解的问题，很多都可以迭代求解，这个题目也一样，小伙伴们可以尝试一下如何将上面的递归改写为迭代算法。

上面的算法提交会TLE，因为数据量是1e5，因此不能使用$O(n^2)$的算法求解。我们想一下超时的问题出现在什么地方？

因为我们每次都要重新求解数组的最小值，浪费了大量的操作。这个题目类似于Leetcode239题，滑动窗口的相关题目，我们要求的最小值也是在滑动的，因此我们可以使用一个单调递增的队列保存滑动窗口的最小值。第一次从0到nums.size() - k + 1这个位置中计算单调递增队列。然后队头元素一定是最小值，因此将队头元素取出加入结果序列res中，然后窗口向下滑动。

算法的**时间复杂度为$O(n)$，空间复杂度为$O(n)$**。

#include<iostream>
#include<vector>
#include<deque>

class Solution {
public:
    vector<int> mostCompetitive(vector<int>& nums, int k) {
        vector<int> res;
        deque<pair<int, int>> queue;
        int begin = 0, end = nums.size() - k + 1;
        while (k) {
            for (int i = begin; i < end; i++) {
                while (!queue.empty() && nums[i] < queue.back().first) queue.pop_back();
                queue.push_back({ nums[i], i });
            }
            int val = queue.front().first, idx = queue.front().second;
            res.push_back(val);
            begin = end;
            queue.pop_front();
            k--;
            end++;
        }
        return res;
    }
};

栈

本题的最妙解法是单调栈求解，时间复杂度和使用单调队列相同，但是代码非常简单。

我们不需要建立额外的单调队列保存最小值，可以直接将结果序列看成一个单调栈。向结果序列中添加元素，如果新加入的元素小于栈顶元素，则栈顶元素出栈，新元素入栈。维护一个单调递增的栈即可。前提是我们要保证剩余元素+栈内元素要大于等于k。

算法的**时间复杂度为$O(n)$，空间复杂度为$O(n)$**。

#include<iostream>
#include<vector>

class Solution {
public:
    vector<int> mostCompetitive(vector<int>& nums, int k) {
        vector<int> res;
        for (int i = 0; i < nums.size(); i++) {
            while (!res.empty() && res.back() > nums[i] && nums.size() - i - 1 + res.size() >= k) res.pop_back();
            if (res.size() < k) res.push_back(nums[i]);
        }
        return res;
    }
};

刷题总结

这个题目是典型的数据结构相关的算法题，难度适中，代码量不多不少，非常适合在面试中考察大家，因此小伙伴们一定要多多练习，自己实现一遍。