题目分析

第222题厉害了，考察的知识点非常丰富，不但有搜索算法，DFS搜索还包含了递归的思想，BFS包含了队列数据结构，还覆盖了位运算和二分查找的思想，这有点类似于完全二叉搜索树。因为一般只有完全二叉树才可能用得到位运算的思想，也只有二叉搜索树才可能用得到二分查找的思想。这个题目将它们融合起来，小伙伴们要好好思考。

DFS

这个题目的重点不是DFS，而且DFS的代码非常简单，就不做过多介绍了。

算法的**时间复杂度为$O(n)$，空间复杂度为$O(log(n))$**，其中n为节点个数。

#include<iostream>
#include<vector>

using namespace std;

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

class Solution {
public:
    int countNodes(TreeNode* root) {
        int res = 0;
        dfs(root, res);
        return res;
    }

    void dfs(TreeNode* node, int& res) {
        if (!node) return;
        res++;
        dfs(node->left, res);
        dfs(node->right, res);
    }
};

BFS

BFS也非常简单，小伙伴们直接看代码。

算法的**时间复杂度为$O(n)$，空间复杂度为$O(n)$**，其中n为节点个数。

#include<iostream>
#include<vector>
#include<deque>

using namespace std;

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

class Solution {
public:
    int countNodes(TreeNode* root) {
        int res = 0;
        deque<TreeNode*> queue = { root };
        while (!queue.empty()) {
            TreeNode* cur = queue.front();
            queue.pop_front();
            if (cur) {
                res++;
                queue.push_back(cur->left);
                queue.push_back(cur->right);
            }
        }
        return res;
    }
};

二分查找+位运算

本题要重点讲解二分查找+位运算的算法。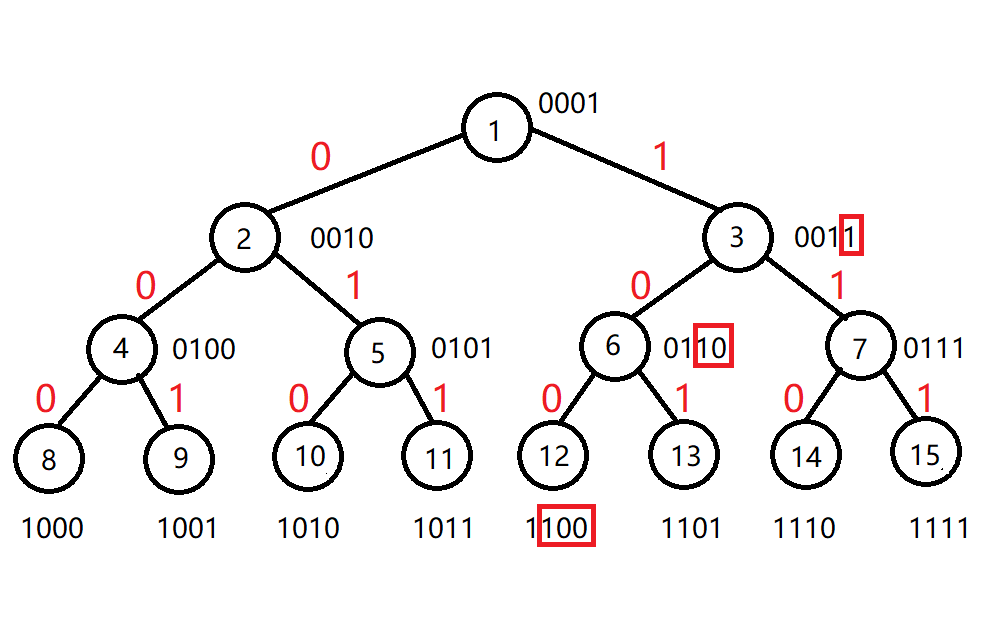

看了上面的图，小伙伴们发现什么规律，是不是从第0层根节点到第k层某节点经过了k个通路，然后这k个通路按照0和1的顺序排列，就是该节点的二进制表示。

因此我们可以确定完全二叉树的层数，然后二分查找最后一层的数量。假定有k层(根节点在第0层)，那么节点数就在$2^k~2^{k + 1} - 1$个。

二分节点数，并且根据节点的二进制表示确定其在左子树还是右子树。

如树有3层，节点数为1101的13号，那么我们看第二位的1，可知它是根节点的右子树中的某个节点。然后看第一位的0，可知它是右子树中的左子树的某个节点。然后看第零位的1可知它是根节点右子树的左子树的右节点。因此如果该节点存在，说明二叉树至少有13个节点，left = mid即可。否则二叉树没有13个节点，right = mid - 1。

因为二分节点数需要log(n)的时间复杂度，从根节点找到该节点也需要log(n)的时间复杂度，因此算法的**时间复杂度为$O(log^{2}(n))$，空间复杂度为$O(1)$**，其中n为节点个数。

#include<iostream>
#include<vector>

using namespace std;

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

class Solution {
public:
    int countNodes(TreeNode* root) {
        if (!root) return 0;
        int layer = -1;
        TreeNode* node = root;
        while (node) {
            layer++;
            node = node->left;
        }
        int left = 1 << layer, right = (1 << (layer + 1)) - 1;
        while (left < right) {
            int mid = (left + right + 1) >> 1;
            node = root;
            for (int i = layer - 1; i >= 0; i--) {
                if (!(mid & (1 << i)) && node->left) node = node->left;
                else if (mid & (1 << i) && node->right) node = node->right;
                else {
                    right = mid - 1;
                    break;
                }
                if (i == 0) left = mid;
            }
        }
        return left;
    }
};

刷题总结

树的位运算表示也非常重要，**如果不用位运算，我们需要递推出节点所在的子树。如13号节点，我们可以先除以2，确定它的父亲节点是6号，因为13 = 6 * 2 + 1，因此13为6号节点的右子树。同理可知6是3号节点的左子树，3是1号根节点的右子树。然后再从根索引到13号节点，来确定13号节点是否存在。这样做时间复杂度多了一次log(n)，而且需要一个堆栈保存13， 6， 3， 1的顺序，方便索引时取出。空间复杂度也会提高到log(n)**。虽然比较麻烦，但是也是一个解决方案，小伙伴们可以尝试能否实现。