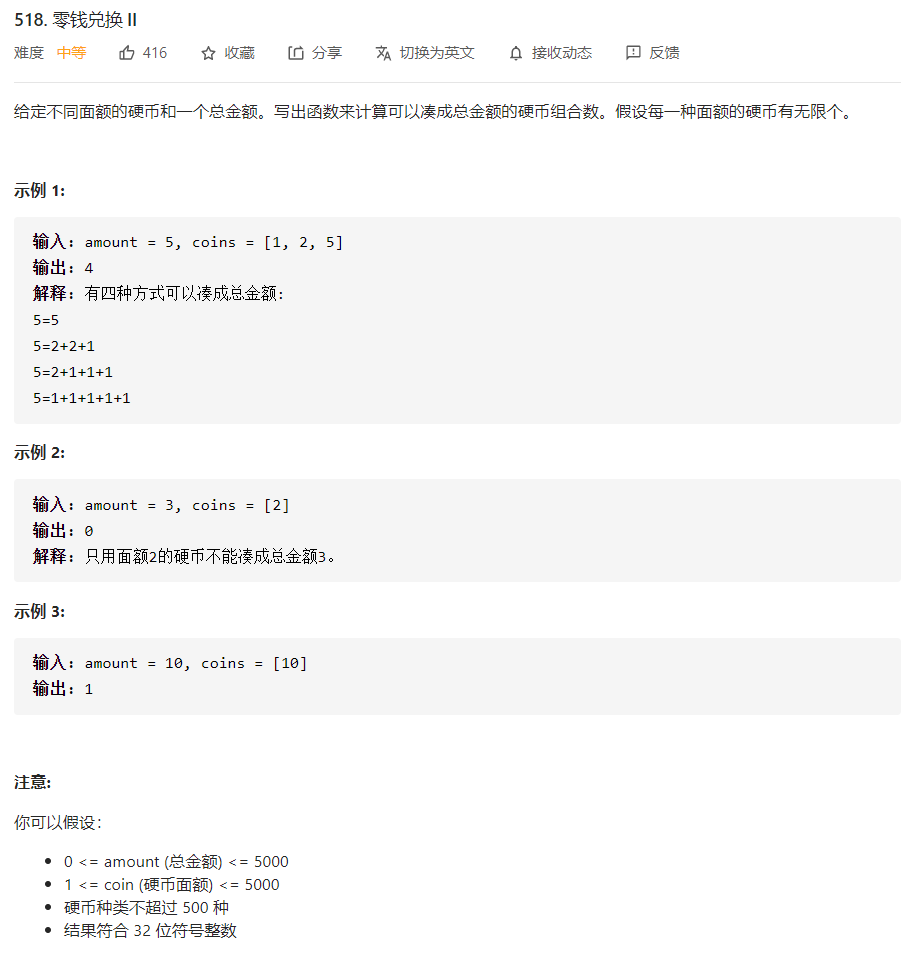
题目分析

这个题目也是一个经典的背包问题，只不过和Leetcode494题不同点在于，本题的硬币数量可以无限个，被称为完全背包，解决思路是类似的，小伙伴们先思考一下如何去解

动态规划

用dp[i][j]表示前i个硬币能凑出j块钱的方案数量，可以不使用第i个硬币，即dp[i - 1][j]，也可以使用第i个硬币，dp[i][j - coins[i]]，在Leetcode第494题中，这个表达式为dp[i - 1][j - coins[i]]，这是两道题目的关键差异。在494题中，一个硬币只能选择一次，只能加上前i - 1个硬币凑出j - coins[i]的方案数，本题可以多次使用，因此无论第i个硬币使用多少次，都可以加上前i个硬币凑出j - coins[i]的方案数，只要再次使用第i个硬币即可。
$$dp[i][j] = dp[i - 1][j] + dp[i][j - nums[i]]$$
因为第i层状态仅与第i - 1层有关，可以使用一维dp进行求解，此时因为使用本层更新后的数据，所以要顺序遍历。

算法的**时间复杂度为$O(n \cdot amount)$，空间复杂度为$O(amount)$**，其中n为硬币种类

下面是Java语言的题解

class Solution {
    public int change(int amount, int[] coins) {
        int[] dp = new int[amount + 1];
        dp[0] = 1;
        for (int coin : coins) {
            for (int i = coin; i <= amount; i++) {
                dp[i] += dp[i - coin];
            }
        }
        return dp[amount];
    }
}

下面是Kotlin语言的题解

class Solution {
    fun change(amount: Int, coins: IntArray): Int {
        val dp = IntArray(amount + 1)
        dp[0] = 1
        for (coin in coins) {
            for (i in coin..amount) {
                dp[i] += dp[i - coin]
            }
        }
        return dp.last()
    }
}

刷题总结

最近Leetcode的每日一题都是背包问题，小伙伴们可以从网上搜索背包九讲相关的知识点进行集中练习，仔细区别各个体型之间的差异。