题目分析

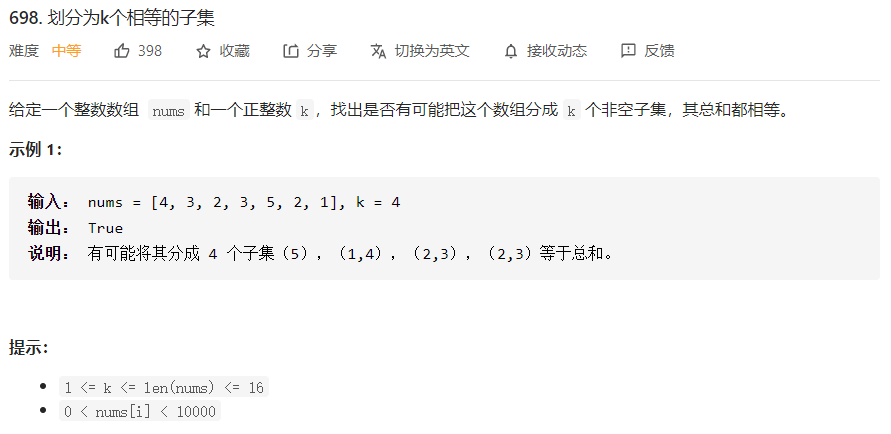
这个题目和前几天做的第473题类似，不过难度要更大一些，在473题中，要使用火柴棒拼成一个正方形，是本题k为4的一个特例。

DFS

本题类似与排列组合题目，n个数，先判断n个数之和是否能被k整除，如果能整除，求出整除后的值mean。然后进行全排列，和小于mean的值则给当前集合添加元素，和等于mean则开始判断下一个集合，和大于mean则说明该排列不符合要求。

算法的**时间复杂度为$O(n!)$，空间复杂度为$O(n)$**，因为n最大可以为16，因此可能会产生TLE的情况，但是存在剪枝操作，因此不会真正进行全排列的操作，所以本题可以勉强通过。

下面是Java语言的题解

class Solution {
    public boolean canPartitionKSubsets(int[] nums, int k) {
        int sums = 0;
        for (int val : nums) {
            sums += val;
        }
        if (sums % k != 0) {
            return false;
        }
        int mean = sums / k;
        return dfs(1, 0, new boolean[nums.length], nums, mean, k);
    }

    private boolean dfs(int layer, int cur, boolean[] visit, int[] nums, int mean, int k) {
        if (layer > k - 1) {
            return true;
        }
        for (int i = 0; i < visit.length; i++) {
            if (!visit[i]) {
                if (cur + nums[i] <= mean) {
                    visit[i] = true;
                    boolean res = cur + nums[i] == mean ? dfs(layer + 1, 0, visit, nums, mean, k) : dfs(layer, cur + nums[i], visit, nums, mean, k);
                    if (res) {
                        return true;
                    }
                    visit[i] = false;
                } else {
                    return false;
                }
            }
        }
        return false;
    }
}

状态压缩DP

状态压缩DP的思想非常巧妙，状态压缩是指用bit位来表示该元素是否已经选择。本题的n最大位16，而int值为32位，因此足够表示16个数，0…0001表示选择了第一个数，0…1010表示选择了第二个数和第四个数。sum[i]表示状态i所选取的数字之和，isSatisfy[i]表示状态i所选取的数字是否有可能满足条件。

其中状态i从0到(1 << n) - 1，然后遍历元素索引j，如果当前状态的第j位为不为0，定义前一个状态为pre = i ^ (1 << j)。说明该状态i可由pre添加第j个元素转化而来，但是此时不一定能够成功转化。如果状态pre是满足条件的，并且sum[pre] % mean + nums[j] <= mean说明本状态可以由pre状态成功转化而来。

算法的时间复杂度为$O(k x 2^n)$，空间复杂度为$O(2^n)$

下面是Java语言的题解

class Solution {
    public boolean canPartitionKSubsets(int[] nums, int k) {
        int sums = 0;
        for (int val : nums) {
            sums += val;
        }
        if (sums % k != 0) {
            return false;
        }
        int length = nums.length;
        int mean = sums / k;
        int bit = 1 << length;
        boolean[] isSatisfy = new boolean[bit];
        int[] sum = new int[bit];
        isSatisfy[0] = true;
        for (int i = 0; i < bit; i++) {
            for (int j = 0; j < length; j++) {
                if ((i & (1 << j)) != 0 && isSatisfy[i ^ (1 << j)] && (sum[i ^ (1 << j)] % mean) + nums[j] <= mean) {
                    isSatisfy[i] = true;
                    sum[i] = sum[i ^ (1 << j)] + nums[j];
                    break;
                }
            }
        }
        return isSatisfy[bit - 1];
    }
}

刷题总结

小伙伴们要仔细比较两中算法在时间复杂度上的差异，并深刻理解$2^n$和$n!$在速度上相差了多少。很多人默认为指数爆炸的时间复杂都最高，其实阶乘的复杂度会更大一些，一般来说1e8是我们写算法题的极限运算量，此时对于指数量级来说，n可以取到26-27左右，但是对于阶乘来说，n只能取到12-13左右，所以对于全排列这类问题，一定要小心谨慎。