线段树

线段树

线段树介绍

  线段树(Segment Tree):是一种进阶的数据结构，因为其是树形结构，且每个节点表示一段连续的线性空间，因此被称为线段树，线段树和树状数组类似，也是非常适用于前缀和的问题。

线段树的应用

前缀和这里就不过多赘述了，感兴趣的小伙伴可以去前一讲树状数组了解。线段树是根据二分法将一个大的区间分成两个子区间，其中大的区间为[left, right]索引和，则左子树表示[left, (left + right) / 2]，右子树表示[(left + right) / 2 + 1, right]。当区间的长度为1时停止划分。

此时查找范围可以按照二分查找的思路，将区间和变为$O(mlog(n))$的时间复杂度，其中m为操作次数，n为数组的长度。修改时，也只需要按照区间中点进行划分，如果索引在左子树，只需要更新左子树的节点值，直到更新到叶子节点(区间长度为1)。

线段树的实现

以leetcode307题为例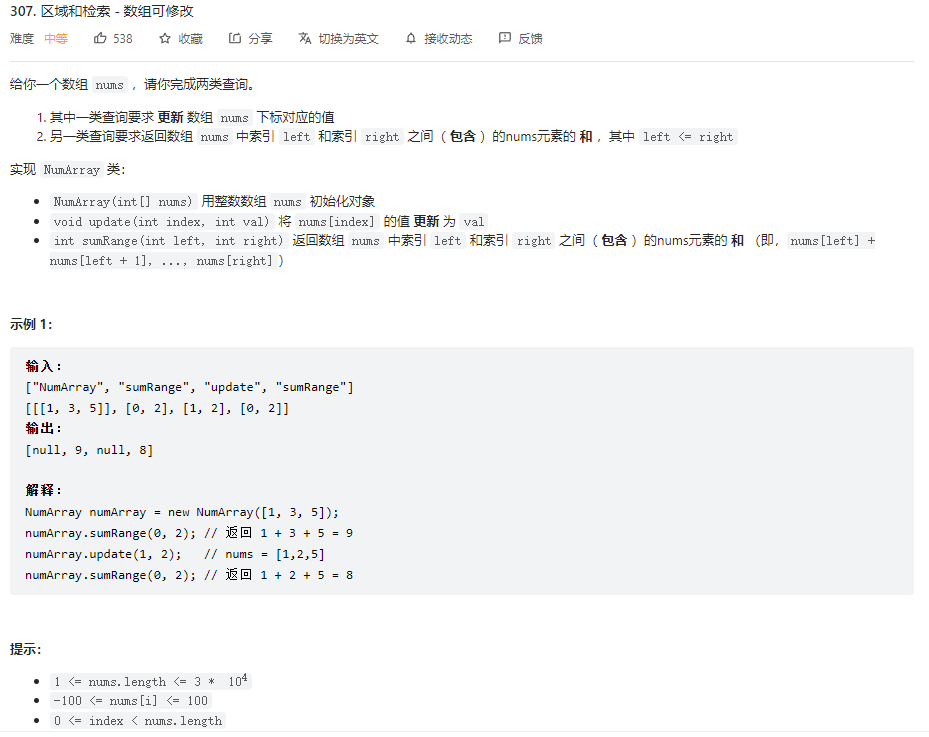

首先要初始化线段树，定义数组长度为length，tree保存线段树的区间和，因此多少个节点就需要开辟多大的数组内存。如何统计出节点数呢？

因为线段树都是二分定义的，因此树的最大深度比最小深度大1，或者相等。因此树的最大深度是$ \left \lceil log(n) \right \rceil $ 因此节点数总数小于 $ 2^{\left \lceil log(n) \right \rceil + 1} < 4n $

而且定义根为node，则左子树的索引为node x 2 + 1，右子树的索引为node x 2 + 2。

class NumArray {
    int length;
    int[] tree;

    public NumArray(int[] nums) {
        length = nums.length;
        tree = new int[length * 4];
        buildTree(0, 0, length - 1, nums);
    }
    
    private void buildTree(int node, int left, int right, int[] nums) {
        if (left == right) {
            tree[node] = nums[left];
            return;
        }
        int mid = (left + right) >> 1;
        int leftNode = node * 2 + 1;
        int rightNode = node * 2 + 2;
        buildTree(leftNode, left, mid, nums);
        buildTree(rightNode, mid + 1, right, nums);
        tree[node] = tree[leftNode] + tree[rightNode];
    }
}

构造完毕后，我们开始修改其中的节点，如果left == right，则说明已经访问到叶子节点，直接赋值即可。否则要判断该索引在树的左侧还是右侧。

public void update(int index, int val) {
    add(0, 0, length - 1, index, val);
}

private void add(int node, int left, int right, int index, int val) {
    if (left == right) {
        tree[node] = val;
        return;
    }
    int mid = (left + right) >> 1;
    int leftNode = node * 2 + 1;
    int rightNode = node * 2 + 2;
    if (index <= mid) {
        add(leftNode, left, mid, index, val);
    } else {
        add(rightNode, mid + 1, right, index, val);
    }
    tree[node] = tree[leftNode] + tree[rightNode];
}

最后我们看一下最复杂的区间求和操作，区间求和分成三种情况讨论。

• 求和区间都在树的左侧，则rRight <= mid，此时只需要找左子树即可。
• 求和区间都在树的右侧，则rLeft > mid，此时只需要找右子树即可。
• 求和区间分布在树的两侧，此时既需要找左子树也需要找右子树。

  public int sumRange(int left, int right) {
      return get(0, 0, length - 1, left, right);
  }
  
  private int get(int node, int left, int right, int rLeft, int rRight) {
      if (left == rLeft && right == rRight) {
          return tree[node];
      }
      int mid = (left + right) >> 1;
      int leftNode = node * 2 + 1;
      int rightNode = node * 2 + 2;
      if (rRight <= mid) {
          return get(leftNode, left, mid, rLeft, rRight);
      } else if (rLeft > mid) {
          return get(rightNode, mid + 1, right, rLeft, rRight);
      } else {
          return get(leftNode, left, mid, rLeft, mid) + get(rightNode, mid + 1, right, mid + 1, rRight);
      }
  }

小结

  上面的代码就是线段树的模板，线段树的时间复杂度为$O(mlog(n))$，空间复杂度为$O(n)$，线段树对于理解树的递归非常有帮助，虽然代码相对复杂，但是理解了其中的原理也是比较容易的，希望大家也能多多练习，顺利写出线段树。