树状数组

发表于 | 分类于 ， | | 本文总阅读数 次
| 字数统计: 1.9k | 阅读时长 ≈ 7
树状数组

树状数组

树状数组介绍

  树状数组(Binary Indexed Tree):是一种进阶的数据结构，英文直译是二叉索引树，因为其结构类似于树，但是保存在数组中，因此常被称为树状数组，在基础的算法中很少使用，因为最近面试笔试题目越来越难、包括做一些比赛都可能会用到这个知识点。如果能在面试中写出树状数组，那一定是相当加分的。

前缀和

讲到树状数组，很难不从前缀和开始说起，说是有一个数组长度为n，我们想求某个区间的和，应该如何实现？BF算法当然可以实现，但是当操作m次时，时间复杂度为$O(mn)$。

如果我们新开一个数组名为cursum，其中索引i表示从索引0到索引i - 1的和，那么某个区间[p, q]的和为cursum[q + 1] - cursum[p]。时间复杂度为$O(max(m, n))$。

前缀和扩展

前缀和相信对于大家来说是非常简单的问题，我们给题目增加一点点难度，如果要求可以修改某一个索引的值呢？

BF算法还是一样，时间复杂度为$O(mn)$，空间复杂度为$O(1)$。但是前缀和的算法，如果想修改索引为i的值，那么从i + 1开始的cursum都需要进行修改。时间复杂度也变成$O(mn)$了。如何降低时间复杂度呢？

树状数组的应用

前缀和为什么这么耗费时间，是因为一旦修改一个数，后面的所有数字都需要牵连一起修改。那么能否有一种数据结构，只修改某一个位置，或者某一些数字即可呢？

我们细品BF和前缀和算法，BF的特点是，每一个索引就是对应的值，因此修改时仅需要单点修改。而前缀和的特点是，每一个索引是前面所有数字之和，因此修改时，要修改后面的所有索引。是不是可以用一种居中的思想，让每一个索引表示部分数字之和呢？

通常的想法是二分，也和计算机中数字的表示相关。

一个正整数x，二进制可以表示为

$$C_n C_{n-1} … C_1 C_0$$

其值等于

$$C_n * 2^n + C_{n - 1} * 2^{n - 1} + … + C_1 * 2^1 + C_0 * 2^0$$

因此我们可以将x拆解成n个数字之和(1, 2, 4, 8, 16, …)，如果前面系数是1则加上该数字，如果系数是0则忽略。我们是不是可以根据二进制中每一位对应的数字来表示连续数字区间的长度。

举个例子，bin(12) = 8 + 4 = 1100，二进制中最后一个1表示4，说明tree[12] = num[8] + num[9] + num[10] + num[11]，四个数之和。

把12的最后一位去掉后，还有8，说明tree[8] = num[0] + num[1] + … + num[7]，八个数之和。

把8的最后一位去掉后，就变成0，可以停止了，因此索引0到索引11的和为tree[12] + tree[8]。

上面是数组的查询，如果搜索m次，可以看出时间是$O(mlog(n))$的，下面看一下数组的修改。

如果修改了索引为3的值，根据bin(3) = 11，最后一个1表示1，那么tree[3] = num[2]，一个数之和。所以tree[3]要进行修改。

3最后一个1进位后，bin(4) = 100，最后一个1表示4，说明tree[4] = num[0] + num[1] + num[2] + num[3]，也包含了num[3]，因此tree[4]也要进行修改。

同理，4最后一个1进位后，bin(8) = 1000，最后一个1表示8，说明tree[8] = num[0] + num[1] + … + num[7]，也包含了num[3]，因此tree[8]也要进行修改。

小伙伴们可能会有疑问，为什么最后一个1进位后就一定会包含该数字呢？下面进行一些证明

这里用lowBit(x)表示x的最后一位。

  1. 先证明

$$x > x + lowBit(x) -lowBit(x + lowBit(x))$$

这是什么意思呢？x + lowBit(x)是进位后的数字，lowBit(x + lowBit(x))是进位后数字表示的连续数字区间长度。因为

$$tree[x + lowBit(x)] = array[x + lowBit(x)] + array[x + lowBit(x) - 1] + … + array[x + lowBit(x) - lowBit(x + lowBit(x)) + 1] $$

因此x必须大于x + lowBit(x) - lowBit(x + lowBit(x))，无法取得等号。

证明原式，即证

$$lowBit(x) < lowBit(x + lowBit(x))$$

显然成立，也可以用一些简单的方法证明

$$\because x = 2^n + 2^m + … + 2^p (n > m > p)$$

$$\therefore lowBit(x) = 2^p $$

$$\therefore x + lowBit(x) = 2^n + 2^m + … + 2^{p + 1} $$

$$\therefore lowBit(x + lowBit(x)) \ge 2^{p + 1} > 2^p = lowBit(x) $$

所以上式得证。

  1. 还需要证明x + t表示的区间内一定不包含x(0 < t < lowBit(x))，两者结合才能说明修改索引x的时候，加上lowBit(x)才能表示包含array[x]的最小集合。

即证$$x \le x + t - lowBit(x + t)$$

即证$$lowBit(x + t) \le t $$

$$\because t < lowBit(x)$$

$$\therefore t = 2^q + 2^r + … + 2^s (p > q > r > s)$$

$$\therefore x + t = 2^n + 2^m + … + 2^p + … + 2^q + 2^r + … + 2^s (n > m > p > q > r > s) $$

$$\therefore lowBit(x + t) = lowBit(t) = 2^s \le 2^q + 2^r + … + 2^s = t $$

所以上式得证。

树状数组的实现

以leetcode307题为例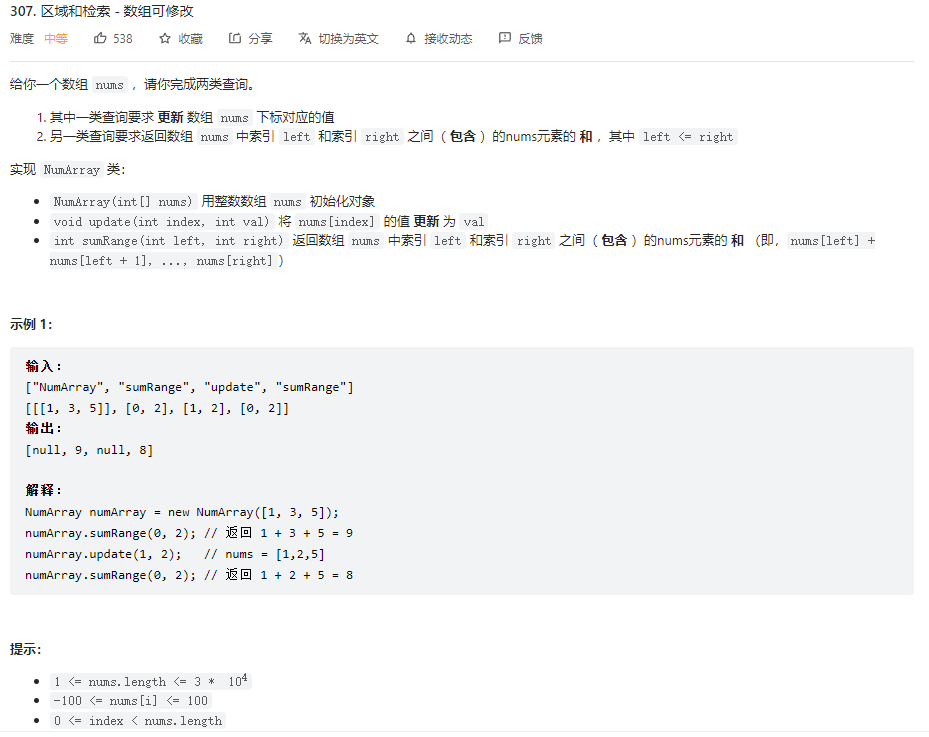
1

首先要初始化树状数组，定义数组长度为length，一个array保存原数组，更新索引时，用于比较与原数组的差异。tree保存树状数组的值。

定义add函数，表示给数组某一位index加上val的值。因此初始化树状数组，就是给第i位添加值为nums[i - 1]的值，注意树状数组是从1开始索引的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class NumArray {
    int length;
    private int[] array;
    private int[] tree;

    public NumArray(int[] nums) {
        length = nums.length;
        array = nums.clone();
        tree = new int[length + 1];
        for (int i = 1; i < length; i++) {
            add(i, nums[i - 1]);
        }
    }
    
    private void add(int index, int val) {
    }
}

下面开始实现add函数，add函数要给tree[index]增加val值，也要给index加上最后一位1增加val值，依次递归。

取出最后一位有一个位运算的技巧，因为负数在二进制中以补码的方式存储，对于负数而言，补码即为反码 + 1，因此x & (-x) 会把x的最低位取出来，所以取最后一位，可以写成x & -x。

1
2
3
4
5
6
7
8
9
private void add(int index, int val) {
    for (; index <= length; index += lowBit(index)) {
        tree[index] += val;
    }
}

private int lowBit(int x) {
    return x & -x;
}

会写add方法以后，本题的update方法也应该不难写出。

1
2
3
4
public void update(int index, int val) {
    add(index + 1, val - array[index]);
    array[index] = val;
}

最后我们要求区间范围，首先求出从0到index - 1的范围和，从index开始，依次减去最后一位1，直到为0结束。

1
2
3
4
5
6
7
private int get(int index) {
    int sum = 0;
    for (; index != 0; index -= lowBit(index)) {
        sum += tree[index];
    }
    return sum;
}

那么本题中的区间范围[left, right]就是区间[0, right] - [0, left - 1]。即get(right + 1) - get(left)

1
2
3
private int sumRange(int left, int right) {
    return get(right + 1) - get(left);
}

小结

  上面的代码就是树状数组的模板，树状数组的时间复杂度为$O(mlog(n))$，空间复杂度为$O(n)$，可以较好的完成前缀和的查找和修改，想要在面试、笔试中发挥亮眼的小伙伴一定要学会它。

-------------本文结束感谢您的阅读-------------
0%