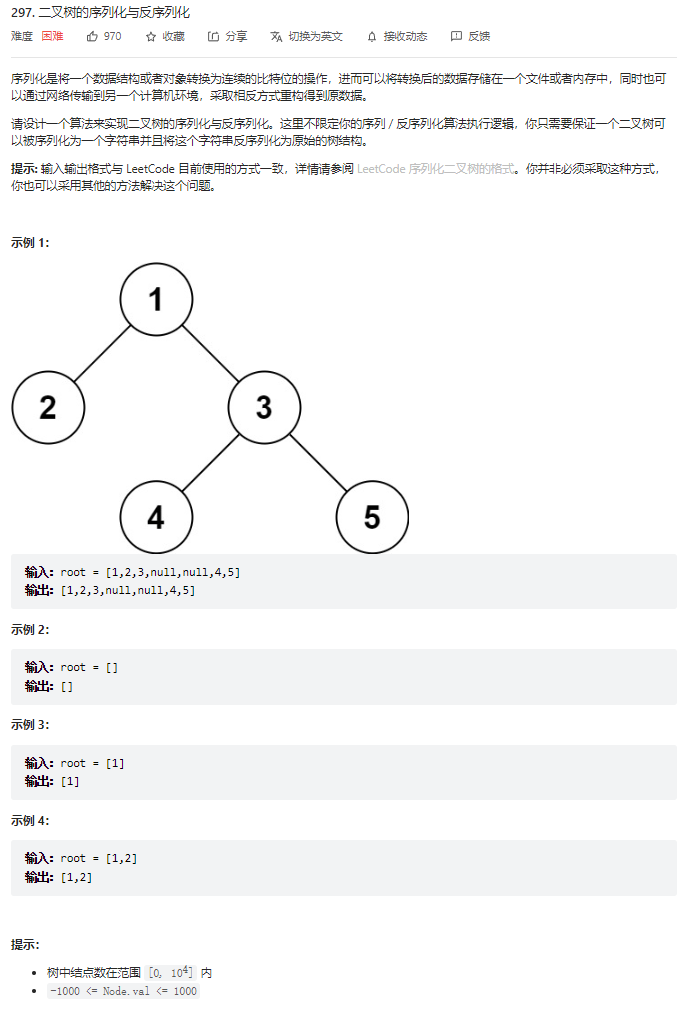
题目分析

在数据通信的过程中，一般传输的类型有byte、short、int、String、byte[]，自定义的数据结构如果想传输，则两边需要协商好如何转化，发送方需要将自定义数据编码为字符串或者byte[]，而接收方需要将字符串或者byte[]解码为数据结构。这种编解码的过程称之为序列化。

前序遍历

我们使用前序遍历将节点保存下来，如果为null则用字符#代替，两个元素之间用逗号表示。

在反序列化的时候也是前序遍历，先读取根节点，然后再遍历左右子树。

算法的**时间复杂度为$O(n)$，空间复杂度为$O(n)$**。

public class Codec {
    private int idx = 0;

    // Encodes a tree to a single string.
    public String serialize(TreeNode root) {
        if (root == null) {
            return "#,";
        }
        return root.val + "," + serialize(root.left) + serialize(root.right);
    }

    // Decodes your encoded data to tree.
    public TreeNode deserialize(String data) {
        idx = 0;
        return preOrder(data.split(","));
    }

    private TreeNode preOrder(String[] data) {
        if (data[idx].equals("#")) {
            idx++;
            return null;
        }
        TreeNode root = new TreeNode(Integer.parseInt(data[idx++]));
        root.left = preOrder(data);
        root.right = preOrder(data);
        return root;
    }
}

后序遍历

我们扩展一下，看下是否能使用后序遍历呢？答案也是可以的，后序遍历是先访问左子树、再访问右子树、最后访问根节点。

因此从后向前就是先访问根节点，再访问右子树，最后访问左子树。所以idx = 元素个数 - 1，从后向前遍历即可。

算法的**时间复杂度为$O(n)$，空间复杂度为$O(n)$**。

public class Codec {
    private int idx = 0;

    // Encodes a tree to a single string.
    public String serialize(TreeNode root) {
        if (root == null) {
            return "#,";
        }
        return serialize(root.left) + serialize(root.right) + root.val + ",";
    }

    // Decodes your encoded data to tree.
    public TreeNode deserialize(String data) {
        String[] strs = data.split(",");
        idx = strs.length - 1;
        return postOrder(strs);
    }

    private TreeNode postOrder(String[] data) {
        if (data[idx].equals("#")) {
            idx--;
            return null;
        }
        TreeNode root = new TreeNode(Integer.parseInt(data[idx--]));
        root.right = postOrder(data);
        root.left = postOrder(data);
        return root;
    }
}

中序遍历

中序遍历不行，因为我们不知道哪一个节点是根节点。

举个例子，下图两个树结构的中序遍历都是”#,C,#,B,#,A,#”，无法反序列化成唯一的树结构。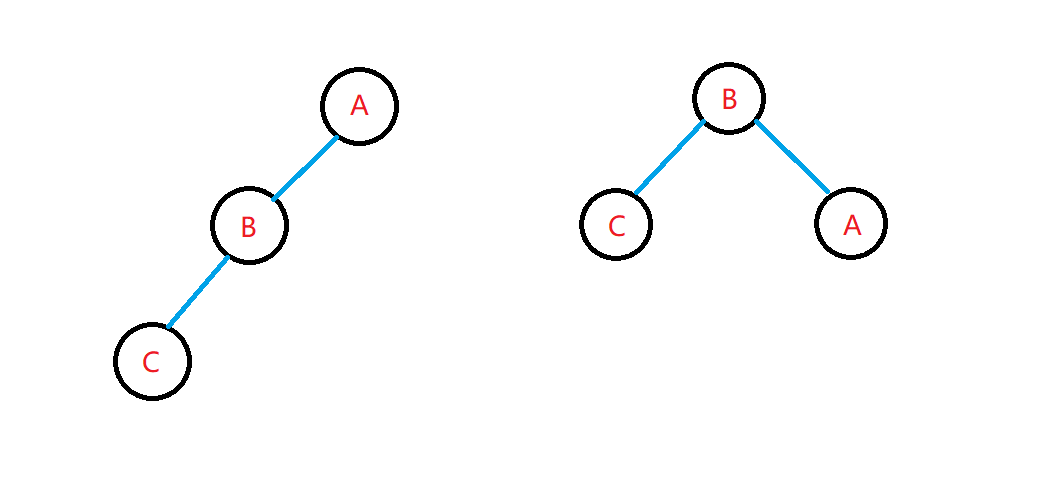

层序遍历

我们使用前序遍历将节点保存下来，如果为null则用字符#代替，两个元素之间用逗号表示。

在反序列化的时候也是前序遍历，先读取根节点，然后再遍历左右子树。

算法的**时间复杂度为$O(n)$，空间复杂度为$O(n)$**。

class Codec {
    // Encodes a tree to a single string.
    public String serialize(TreeNode root) {
        StringBuilder builder = new StringBuilder();
        LinkedList<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        while (!queue.isEmpty()) {
            int size = queue.size();
            while (size-- > 0) {
                TreeNode current = queue.removeFirst();
                if (current == null) {
                    builder.append("#,");
                } else {
                    builder.append(current.val).append(",");
                    queue.addLast(current.left);
                    queue.add(current.right);
                }
            }
        }
        return builder.toString();
    }

    // Decodes your encoded data to tree.
    public TreeNode deserialize(String data) {
        String[] strs = data.split(",");
        if (strs[0].equals("#")) {
            return null;
        }
        TreeNode root = new TreeNode(Integer.parseInt(strs[0]));
        LinkedList<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        int idx = 1;
        while (!queue.isEmpty()) {
            int size = queue.size();
            while (size-- > 0) {
                TreeNode current = queue.removeFirst();
                if (strs[idx].equals("#")) {
                    current.left = null;
                    idx++;
                } else {
                    current.left = new TreeNode(Integer.parseInt(strs[idx++]));
                    queue.add(current.left);
                }
                if (strs[idx].equals("#")) {
                    current.right = null;
                    idx++;
                } else {
                    current.right = new TreeNode(Integer.parseInt(strs[idx++]));
                    queue.add(current.right);
                }
            }
        }
        return root;
    }
}

刷题总结

序列化的题目难度一般，面试也一般不会考到，但是对于加深对数据结构和递归思想的了解非常有帮助。