发表于 | 分类于 ， |
| 字数统计: 2k | 阅读时长 ≈ 10
MLP(Multi-Layer Perceptron)

mlp

原理解读

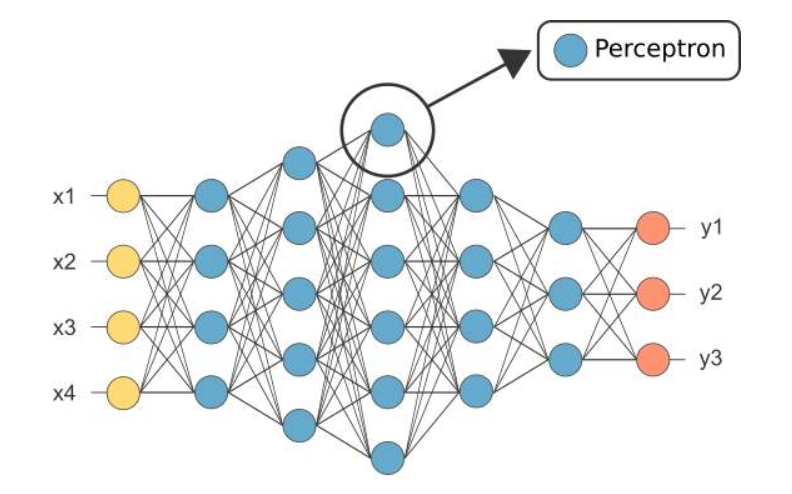
  MLP(Multi-Layer Perceptron):多层感知机**本质上是一种全连接的深度神经网络(DNN)**，感知机只有一层功能神经元进行学习和训练，其能力非常有限，难以解决非线性可分的问题。为了解决这个问题，需要考虑使用多层神经元进行学习。

阅读全文 »

发表于 | 分类于 ， |
| 字数统计: 1.4k | 阅读时长 ≈ 6
逻辑回归(Logistics Regression)

lr

原理解读

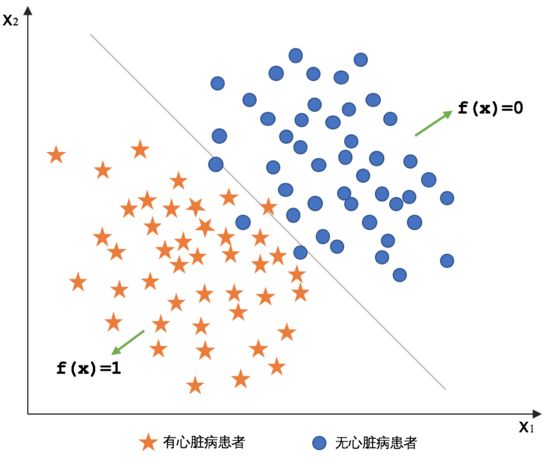
  逻辑回归(Logistics Regression):是一种广义线性回归，都具有 w’x+b，其中w和b是待求参数，其区别在于他们的因变量不同，多重线性回归直接将w’x+b作为因变量，即y =w’x+b，而logistic回归则通过函数g将w’x+b对应一个隐状态p，p =g(w’x+b),然后根据p 与1-p的大小决定因变量的值。如果g是logistic函数，就是logistic回归。

阅读全文 »

发表于 | 分类于 ， |
| 字数统计: 1.5k | 阅读时长 ≈ 6
朴素贝叶斯

bayes

原理解读

  朴素贝叶斯:基于贝叶斯定理，采用了属性条件独立性假设，对已知类别，假设所有属性相互独立，也就是假设每个属性独立地对分类结果发生影响。发源于古典数学理论，而且所需估计的参数很少，算法也较为简单，但是正是因为其假设属性之间相互独立，因此在实际应用中往往是不成立的，所以给模型的正确性带来了一定的影响。

阅读全文 »

发表于 | 分类于 ， |
| 字数统计: 2.3k | 阅读时长 ≈ 10
决策树(Decision Tree)

dt

原理解读

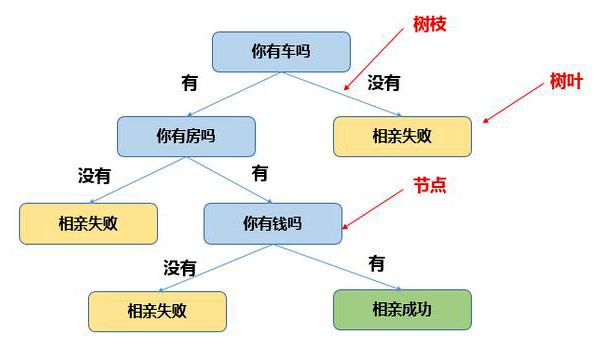
  决策树(Decision Tree):是在已知各种情况发生概率的基础上，直观运用概率分析的一种图解法。决策树是一种树形结构，其中每个内部节点表示一个属性上的测试，每个分支代表一个测试输出，每个叶节点代表一种类别。由于这种决策分支画成图形很像一棵树的枝干，故称决策树。

阅读全文 »

发表于 | 分类于 ， |
| 字数统计: 1.3k | 阅读时长 ≈ 6
Fisher线性判别

fisher

原理解读

  Fisher线性判别:由Fisher于1936年提出，是一种经典的线性学习方法，其根据方差分析的思想建立起来的一种线性判别法，该判别方法对总体的分布不做任何要求。

阅读全文 »

发表于 | 分类于 ， |
| 字数统计: 829 | 阅读时长 ≈ 3
KNN(K Nearest Neighbor)

knn

原理解读

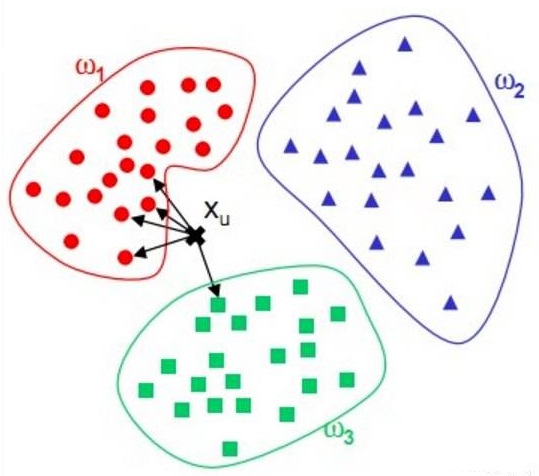
  KNN(K Nearest Neighbor):又称K近邻，是一种基本分类方法，给定测试实例，基于某种距离度量找出训练集中与其最靠近的k个实例点，然后基于这k个最近邻的信息使用投票法，即选择这k个实例中出现最多的标记类别作为分类结果。

阅读全文 »

发表于 | 分类于 ， |
| 字数统计: 898 | 阅读时长 ≈ 4
DE

差分进化算法

背景介绍

  DE(Differential Evolution Algorithm):是一种高效的全局优化算法。它也是基于群体的启发式搜索算法，群中的每个个体对应一个解向量。差分进化算法的进化流程则与遗传算法非常类似，都包括变异、杂交和选择操作，但这些操作的具体定义与遗传算法有所不同。

核心思想

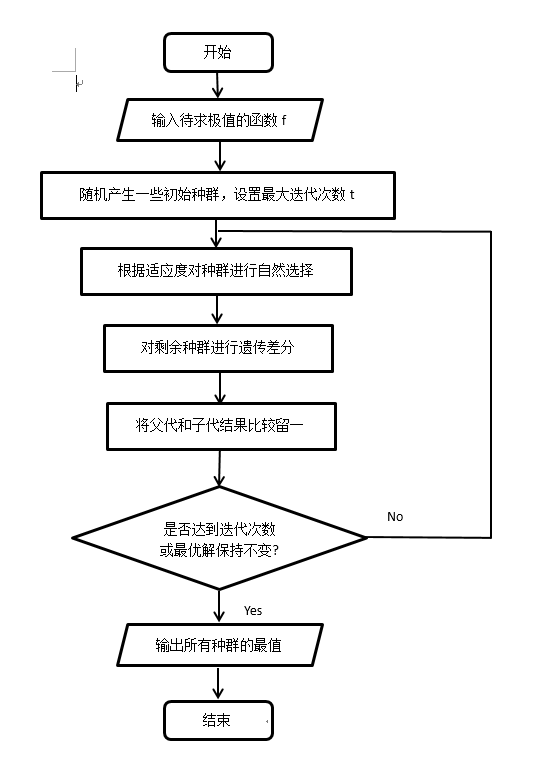
  1. 随机产生一些初始种群

  2. 根据适应度对种群采用某种方式进行自然选择

  3. 对选择剩余的种群进行差分遗传，产生新的种群

  4. 对父代和子代留一处理，回到步骤2，直到满足某个终止条件

  5. 此时剩余的是适应度较好的种群，比较可得该算法的最优解

算法流程

DE

代码实战

代码中所用测试函数可以查看相关文档，测试函数(Test Function)

DE_main.m

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
clear;clc;close all;
%自变量取值范围
range_x=[ones(1,1),-ones(1,1)]*500;
%维度
n=size(range_x,1);
%种群数量
gn=100;
%迭代次数
times=1000;
%交叉概率
cr=0.5;
%随机产生一些种群
group=zeros(n,gn);
for k=1:n
    group(k,:)=(rand(1,gn))*(range_x(k,2)-range_x(k,1))+range_x(k,1);
end
%设置当前最优解
best_value=zeros(1,times);
tic;
for k=1:times
    for i=1:gn
        %基因重组的过程中可能发生染色体变异
        exchange=randperm(gn,3);
        h=group(:,exchange(1))+rand(1)*(group(:,exchange(2))-group(:,exchange(3)));
        h(h>500)=500;
        h(h<-500)=-500;
        v=group(:,i);
        %染色体交换,保留的物种产生后代时发生基因重组
        for j=1:n
            if cr>rand(1)
                v(j)=h(j);
            end
        end
        if f(v)<f(group(:,i))
            group(:,i)=v;
        end
    end
    best_value(k)=min(f(group));
    if k>100&&abs(best_value(k)-best_value(k-100))<1e-5
        break;
    end
end
time=toc;
disp(['用时：',num2str(time),'秒'])
[mini,index]=min(f(group));
disp(['fmin=',num2str(mini)]);
for k=1:n
    disp(['x',num2str(k),'=',num2str(group(k,index))]);
end
if n==1
    hold on;
    plot(group(index),mini,'ro');
    plot_x=range_x(1):(range_x(2)-range_x(1))/1000:range_x(2);
    plot_y=f(plot_x);
    plot(plot_x,plot_y);
    text((range_x(1)+range_x(2))/2,max(plot_y)+0.1*(max(plot_y)-min(plot_y)),['用时：',num2str(time),'秒']);
    hold off;
end
if n==2
    %所求最小值的函数
    func=@(x1,x2)x1.*sin(sqrt(abs(x1)))+x2.*sin(sqrt(abs(x2)));
    plot_x=range_x(1,1):(range_x(1,2)-range_x(1,1))/1000:range_x(1,2);
    plot_y=range_x(2,1):(range_x(2,2)-range_x(2,1))/1000:range_x(2,2);
    [plot_x,plot_y] =meshgrid(plot_x,plot_y);
    plot_z=func(plot_x,plot_y);
    surf(plot_x,plot_y,plot_z);
    xlabel('x1');
    ylabel('x2');
    zlabel('y');
    hold on;
    plot3(group(1,index),group(2,index),mini,'ko')
    text((range_x(1,1)+range_x(1,2))/2,(range_x(2,1)+range_x(2,2))/2,max(max(plot_z))+0.5*(max(max(plot_z))-min(min(plot_z))),['用时：',num2str(time),'秒']);
    hold off;
end

f.m

1
2
3
4
5
6
function res=f(x)
func=@(x)(x).*sin(sqrt(abs(x)));
res=zeros(1,size(x,2));
for i=1:size(x,1)
    res=res+func(x(i,:));
end



实验结果

DE
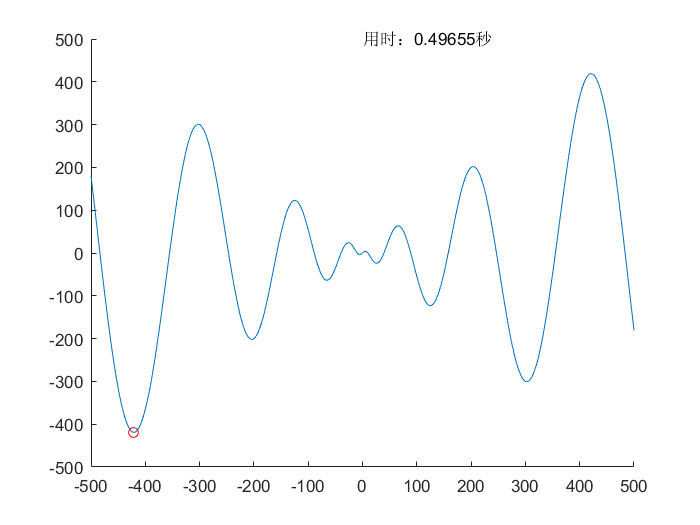
$$f(x)=x \cdot \sin(\sqrt{\lvert x \rvert}) \ , \ x \in [-500,500]$$

$$理论值：f(x)_{min}=f(-420.96874592006)=-418.982887272434$$

$$所求值：f(x)_{min}=f(-420.975929624477)=-418.982887272434$$

性能比较

  • 优点：
    • 受到参数影响较小
    • 不会产生早熟收敛问题
    • 适用于多维的最优值求解
    • 从群体出发，具有并行性
    • 算法不依赖初始种群的选择
    • 可用于求解复杂的非线性优化问题
    • 使用概率机制进行迭代，具有随机性
    • 具有可扩展性，容易与其他算法结合
  • 缺点：
    • 对问题编码表示较为困难
    • 因为有大量的比较和选择，可能速度稍慢于遗传算法

发表于 | 分类于 ， |
| 字数统计: 1.6k | 阅读时长 ≈ 5
Global Search Algorithm Comparison

全局搜索算法比较

全局搜索

  梯度方法，牛顿法，共轭梯度法，拟牛顿法等，能够从初始点出发，产生一个迭代序列。但是很多时候，往往只能收敛到局部极小点。因此为了保证算法能够收敛到全局最小点，需要借助于全局搜索算法来实现。

阅读全文 »

发表于 | 分类于 ， |
| 字数统计: 1.4k | 阅读时长 ≈ 6
Nelder-Mead

单纯形法

背景介绍

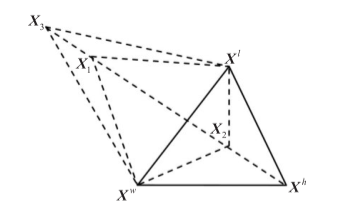
  Nelder-Mead:单纯形法秉承保证每一次迭代比前一次更优的基本思想，先找出一个基本可行解，看是否是最优解，若不是，则按照一定法则转换到另一改进后更优的基本可行解，再鉴别，若仍不是，则再转换，按此重复进行。因基本可行解的个数有限，故经有限次转换必能得出问题的最优解。

阅读全文 »

发表于 | 分类于 ， |
| 字数统计: 979 | 阅读时长 ≈ 4
PSO

粒子群算法

背景介绍

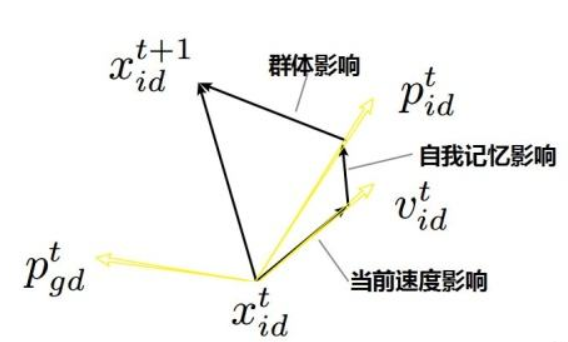
  PSO(Particle Swarm Optimization):受到飞鸟集群活动的规律性启发，进而利用群体智能建立的一个简化模型。粒子群算法在对动物集群活动行为观察基础上，利用群体中的个体对信息的共享使整个群体的运动在问题求解空间中产生从无序到有序的演化过程，从而获得最优解。

阅读全文 »
© 2023 USTCcoder
本站访客数 人 本站总访问量 次
0%