背景介绍
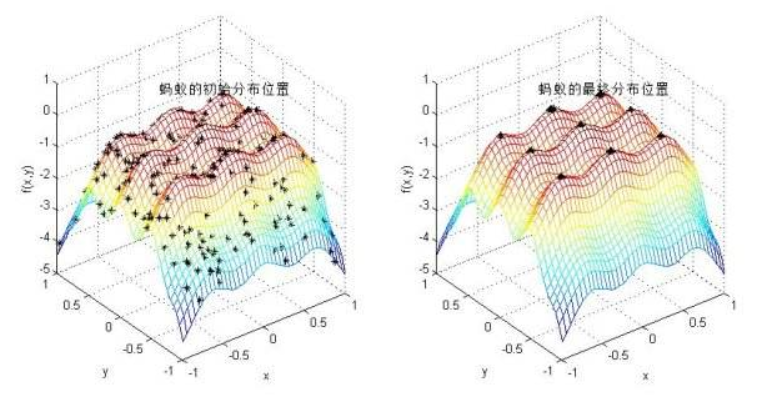
ACO(ant colony optimization):研究蚂蚁觅食的过程中，发现单个蚂蚁的行为比较简单，但是蚁群整体却可以体现一些智能的行为。例如蚁群可以在不同的环境下，寻找最短到达食物源的路径。蚂蚁会在其经过的路径上释放一种可以称之为信息素的物质，蚁群内的蚂蚁对信息素具有感知能力，它们会沿着信息素浓度较高路径行走，而每只路过的蚂蚁都会在路上留下信息素，形成一种类似正反馈的机制。
免疫算法(IA)
背景介绍
IA(Immune Algorithm):免疫算法基于生物免疫系统的基本机制，模仿了人体的免疫系统，解决了遗传算法的早熟收敛问题。因为免疫系统具有辨识记忆的特点，所以可以更快识别群体，面对待求解问题时，相当于面对各种抗原，可以提前注射疫苗抑制退化问题，从而更加保持优胜劣汰的特点。
遗传算法(GA)
背景介绍
GA(Genetic Algorithm):是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，不需要确定的规则就能自动获取和指导优化的搜索空间，自适应地调整搜索方向，是一种通过模拟自然进化过程搜索最优解的方法。
模拟退火算法(SA)
背景介绍
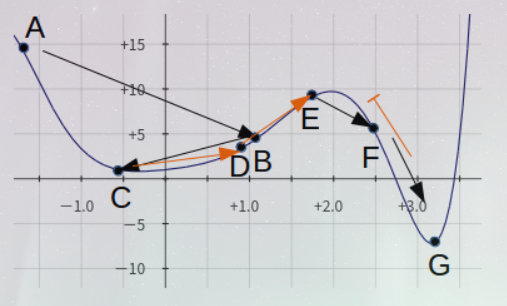
SA(Simulate Anneal):是一种基于Mentcarlo迭代求解法的一种启发式随机搜索方法，基于物理中固体物质的退火过程与一般组合优化问题之间的相似性，通过模拟退火过程，用来在一个大的搜寻空间内找寻命题的最优解（或近似最优解）。
测试函数(Test Function)
原理介绍
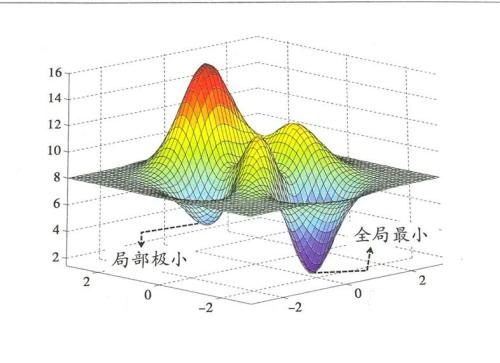
Test Function:对于全局最优解来说，测试函数的选择是至关重要的，测试函数的好坏往往可以体现出搜索算法的优劣。有时性能一般的算法在某个特定的函数下发挥的很好，但是在别的函数下就很难搜索到全局最优解。因此我们需要设计各种测试函数，从搜索效率，搜索精度，适应程度多个方面综合比较各个算法，只有这样，在今后的使用中才能得心应手。
聚类算法比较(Clustering Algorithms Comparison)
无监督学习
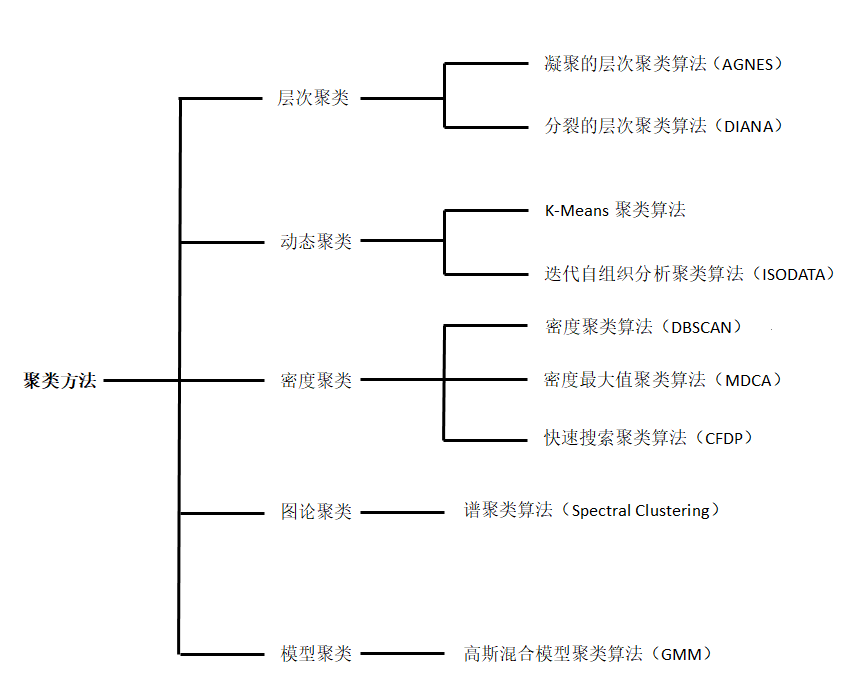
现实生活中常常会缺乏足够的先验知识，因此难以人工标注类别或进行人工类别标注的成本太高。很自然地，我们希望计算机能代我们完成这些工作，或至少提供一些帮助。根据类别未知(没有被标记)的训练样本解决模式识别中的各种问题，称之为无监督学习。
高斯混合模型聚类(GMM)
原理解读
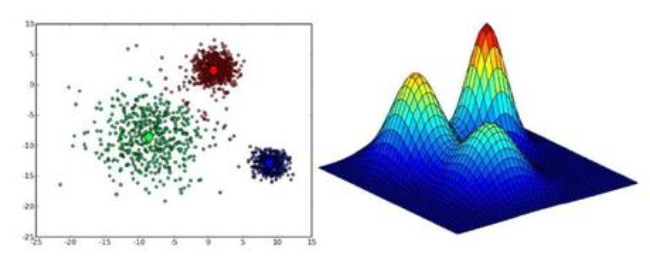
GMM(Gaussian Mixture Model,):是一个将事物分解为若干的基于高斯概率密度函数（正态分布曲线）形成的模型，混合高斯分布( MoG )由多个混合成分组成，每一个混合成分对应一个高斯分布。当聚类问题中各个类别的尺寸不同、聚类间有相关关系的时候，往往使用 MoG 更合适。
谱聚类(Spectral Clustering)
原理解读
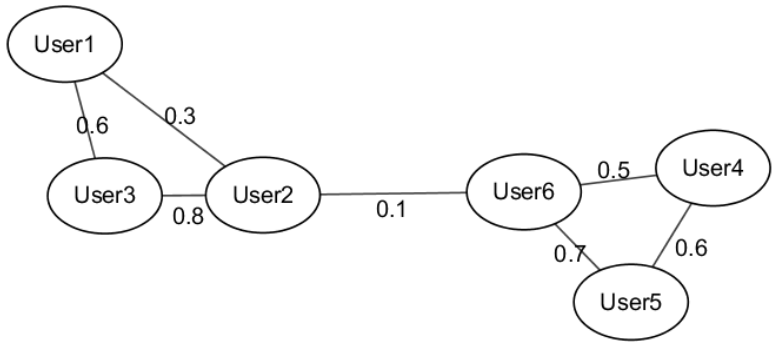
Spectral Clustering:是一种基于图论的聚类算法，第一步是构图：将数据集中的每个对象看做空间中的点V，将这些点之用边E连接起来，距离较远的两个点之间的边权重值较低、距离较近的两个点之间的边权重值较高，这样就构成了一个基于相似度的无向权重图G(V,E)。第二步是切图：按照一定的切边规则将图切分为不同的子图，规则是使子图内的边权重和尽可能大，不同子图间的边权重和尽可能小，从而达到聚类目的。
快速搜索聚类(CFDP)
原理解读
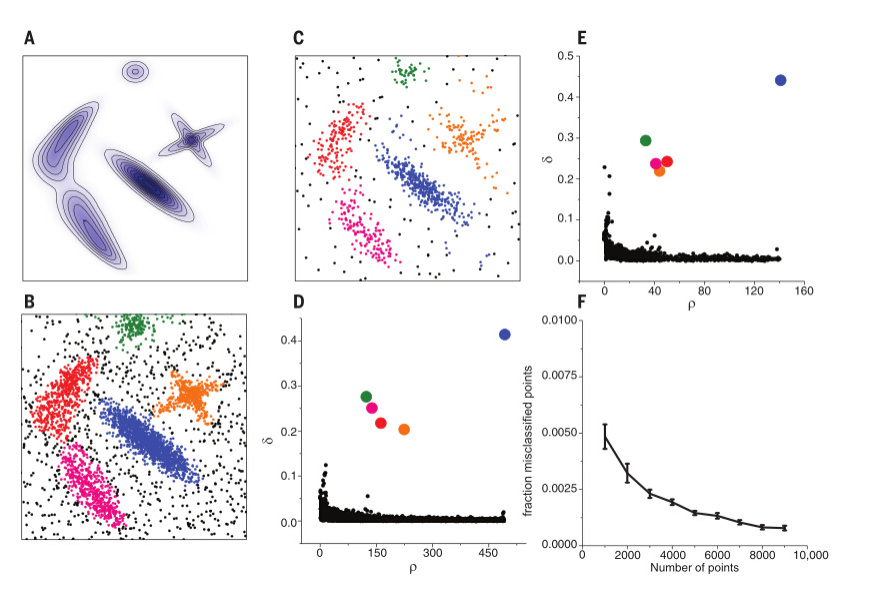
CFDP(Clustering By Fast Search And Find Of Density Peaksd):经典的聚类算法K-means不能检测非球面类别的数据分布，DBSCAN必须指定一个密度阈值，CFDP通过对两种方法的改善，选择每个区域密度最大值，根据密度选择周围点的归属。
密度最大值聚类(MDCA)
原理解读
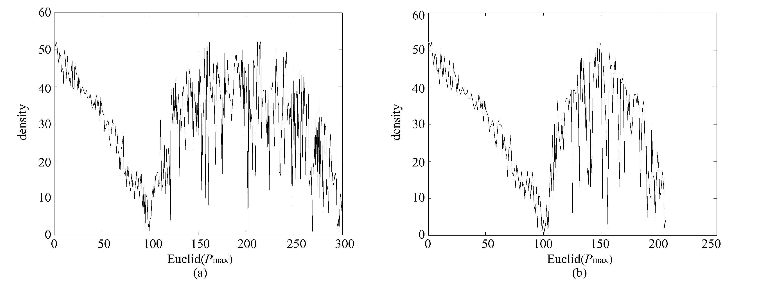
MDCA(Maximum Density Clustering Application):将基于密度的思想引入到划分聚类中，使用密度而不是初始质心作为考察簇归属情况的依据，能够自动确定簇数量并发现任意形状的簇。MDCA一般不保留噪声，因此也避免了由于阈值选择不当而造成大量对象丢弃情况。