原理解读
ISODATA(Iterative Selforganizing Data Analysis) :在k-均值算法的基础上,增加对聚类结果的合并和分裂两个操作,当聚类结果某一类中样本数太少,或两个类间的距离太近,或样本类别远大于设定类别数时,进行合并,当聚类结果某一类中样本数太多,或某个类内方差太大,或样本类别远小于设定类别数时,进行分裂。
核心思想
1. 初始常量(c0,n0,dmin,dmax,T)
c0:希望得到的聚类数
n0:每类的样本数
dmin:最小类间距离
dmax:最大类内距离
T:最大迭代次数
2. 最小类间距离
$$d_{min}=\underset{C_i,C_j \subseteq C}{min}{d( \overline {C_i},\overline {C_j} )} \ , \ 其中\overline {C_i}=\frac {1}{\lvert C_i \rvert}\underset{x_i \in C_i}{\sum}{x_i}$$
3. 最大类内距离
$$d_{max}=\underset{C_i \subseteq C}{max} \ \frac {1}{\lvert {C_i} \rvert}\underset{x_i \in C_i}{\sum}{d( x_i,\overline C_i )} \ , \ 其中\overline {C_i}=\frac {1}{\lvert C_i \rvert}\underset{x_i \in C_i}{\sum}{x_i}$$
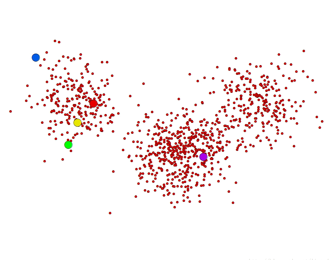 初始时刻状态 初始时刻状态 |
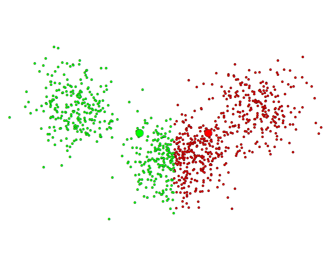 第一次迭代后 第一次迭代后 |
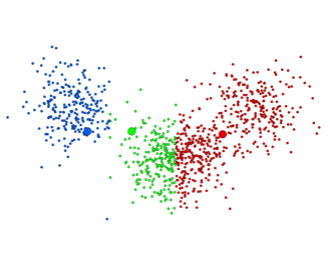 第二次迭代后 第二次迭代后 |
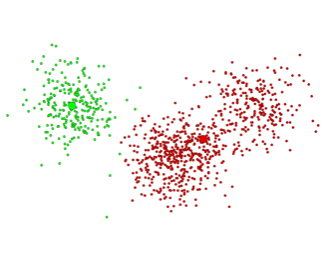 第三次迭代后 第三次迭代后 |
 第四次迭代后 第四次迭代后 |
 第五次迭代后 第五次迭代后 |
4. 判断是否达到分裂条件
- 当前类别数是否小于希望得到聚类数的一半
- 当前每一类的数目是否大于每类样本数的二倍
- 当前类内距离是否大于最大类内距离
5. 分裂不满足条件的类别,回到步骤2,直到满足某个终止条件
6. 判断是否达到合并条件
- 当前类别数是否大于希望得到聚类数的二倍
- 当前每一类的数目是否小于每类样本数的一半
- 当前类间距离是否小于最小类间距离
7. 合并不满足条件的类别,回到步骤2,直到满足某个终止条件
算法流程
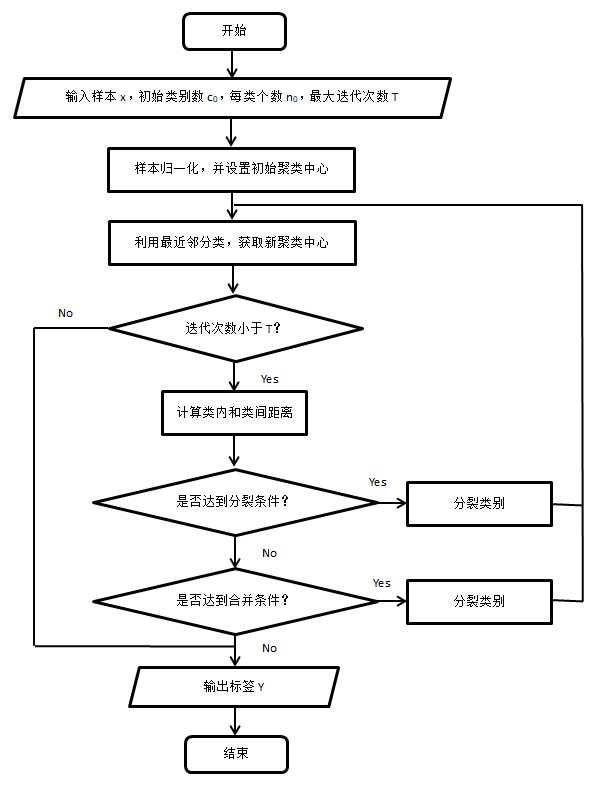
代码实战
代码中所用数据集可以查看相关文档,数据集(Data Set)
ISODATA_main.m
1 | clear;clc;close all; |
ISODATA_classify.m
1 | function [y,class_num,class_center]=ISODATA_classify(x_scale,sample_num,hope_class_num,hope_num,max_class_inner_distance,min_class_between_distance,times) |
ISODATA_display.m
1 | function ISODATA_display(x,y,class_center,sample_num,class_num) |
实验结果
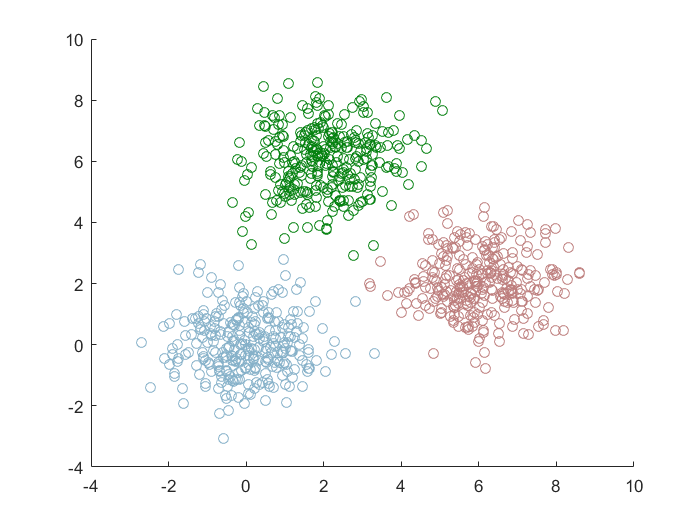
性能比较
- 优点:
- 大数据集时,对噪声数据不敏感
- 可以动态调整类别个数和类别中心
- 在先验知识不足的情况下有较好的分类能力
- 缺点:
- 对初始中心点敏感
- 算法复杂,分类速度较慢
- 只适合分布呈凸型或者球形的数据集
- 对于高维数据,距离的度量并不是很好