密度最大值聚类方法

原理解读

MDCA(Maximum Density Clustering Application):将基于密度的思想引入到划分聚类中，使用密度而不是初始质心作为考察簇归属情况的依据，能够自动确定簇数量并发现任意形状的簇。MDCA一般不保留噪声，因此也避免了由于阈值选择不当而造成大量对象丢弃情况。

核心思想

1.最大密度点：可用K近邻距离之和的倒数表示密度
$$\rho_{max}={ \rho_{x} | x \in C, \forall x_i \in C, \rho_(x) \ge \rho_(x_i) } \ , \ 其中C为数据集$$

2. 密度曲线：根据所有对象与x的欧式距离对数据集重新排序
$$S_{\rho_{max}}={x_1 , x_2 , \cdots , x_n | d(x,x_1) \leq d(x,x_2) \leq \cdots \leq d(x,x_n) }$$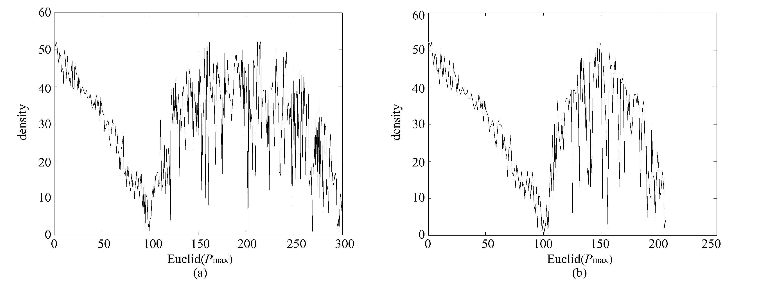
MDCA

3. 将密度曲线中第一个谷值之前的数据归为一类，并将其剔除

4. 重复步骤1，2，3直到所有的点都在ρ₀之下或者ρ₀之上

5. 两个簇C_i和C_j，用最近样本距离作为簇间距离
$$d(c_i,c_j)=\underset{x_i \in C_i,x_j \in C_j}{\min}d(x_i,x_j)$$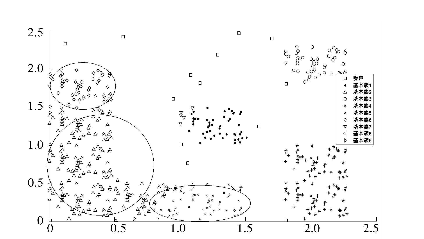
MDCA

6. 根据簇间距离阈值d₀，判断是否需要合并两类

算法流程

MDCA

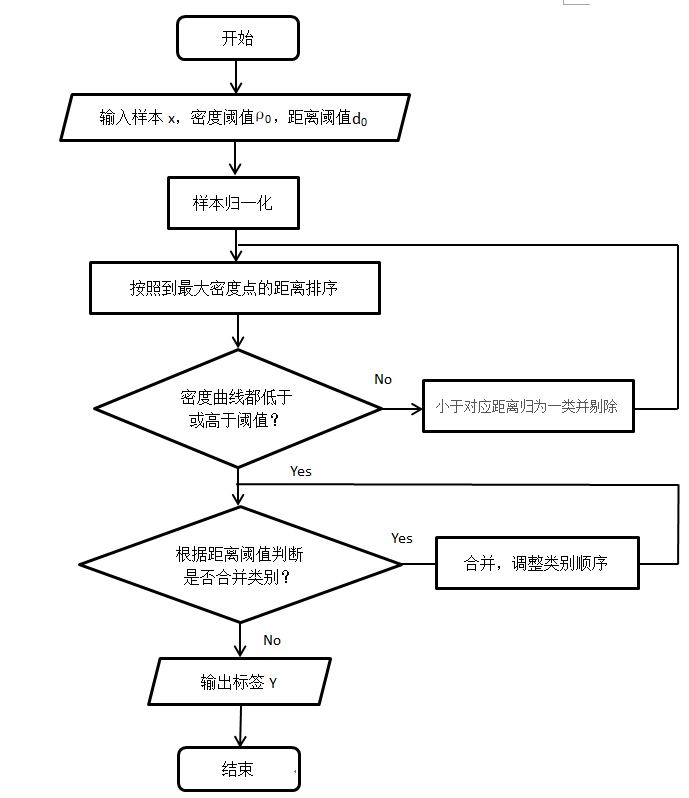
代码实战

代码中所用数据集可以查看相关文档，数据集(Data Set)

MDCA_main.m

clear;clc;close all;
load('..\\cluster_gauss.mat');
%输入x的矩阵
x=data;
randIndex = randperm(size(x,2));
x=x(:,randIndex);
%样本数
sample_num=size(x,2);
%判断密度时检测周围点的个数
k=5;
%最小阈值密度
density_min=25000;
%最小阈值距离
distance_min=0.1;
%特征数目
feat_num=size(x,1);
%尺度缩放到0-1
x_scale=zeros(size(x));
for i=1:feat_num
    x_scale(i,:)=(x(i,:)-min(x(i,:)))/(max(x(i,:))-min(x(i,:)));
end
[y,class_num]=MDCA_classify(x_scale,sample_num,k,density_min,distance_min);
% 如果数据的特征是二维的，可以绘图表示
if feat_num==2
    MDCA_display(x,y,sample_num,class_num);
else
    disp('The Feature Is Not Two-Dimensional');
end

MDCA_classify.m

function [y,class_num]=MDCA_classify(x_scale,sample_num,k,density_min,distance_min)
class_num=1;
y=zeros(1,sample_num);
%p为每个样本的密度
p=zeros(1,sample_num);
%distance(i,j)代表第i个样本到第j个样本的距离
distance=zeros(sample_num);
%利用k近邻均值定义密度较好，不会出现很多密度相同的点。如果采用半径内个数的定义方法，可能一块区域会出现很多的类别
for i=1:sample_num
    distance(i,:)=sum((x_scale-repmat(x_scale(:,i),1,sample_num)).^2);
    temp=sort(distance(i,:));
    p(i)=k./sum(distance(i,distance(i,:)<=temp(k)));
end        
[y,class_num]=MDCA_findclass(y,p,distance,density_min,class_num);    
%设置两个标置位
while 1
    flag_2=0;
    for i=1:class_num
        flag_1=0;
        for j=i+1:class_num
            if min(min(distance(y==i,y==j)))<=distance_min
                y(y==j)=i;
                y(y>j)=y(y>j)-1;
                class_num=class_num-1;
                flag_1=1;
                break;
            end
        end
        if flag_1==1;
            break;
        end
        flag_2=1;
    end
    if flag_2==1
        break;
    end
end
loc=find(y~=0);
[temp,tem]=min(distance(y==0,y~=0),[],2);
y(y==0)=y(loc(tem)).*(temp<=distance_min)';

MDCA_findclass.m

function [y,class_num]=MDCA_findclass(y,p,distance,density_min,class_num)
tem=find(y==0);
p_temp=p(tem);
%找到最大的密度点
p_max=tem(find(p_temp==max(p_temp),1));
%按照到最大密度点的距离从小到大排序
[~,b]=sort(distance(p_max,tem));
temp=tem(b);
curve=p(temp);
if max(curve)>density_min
    loc=find(curve<=density_min);
    if ~isempty(loc)&&length(loc)>=2
        for i=1:length(loc)-1
            if loc(i+1)-loc(i)<=2
                break;
            end
        end
        y(temp(1:loc(i)))=class_num;
        [y,class_num]=MDCA_findclass(y,p,distance,density_min,class_num+1);
        return;
    end
end

MDCA_display.m

function MDCA_display(x,y,sample_num,class_num)
figure;
hold on;
for i=1:class_num
    color_bar(i,:)=[rand(1),rand(1),rand(1)];
end
for i=1:sample_num
    if y(i)==0
        %画出噪声点，用*表示
        plot(x(1,i),x(2,i),'k*')
    else
        %画出每一类的样本数据，用o表示
        plot(x(1,i),x(2,i),'color',color_bar(y(i),:),'marker','o');
    end
end
hold off;

实验结果

MDCA

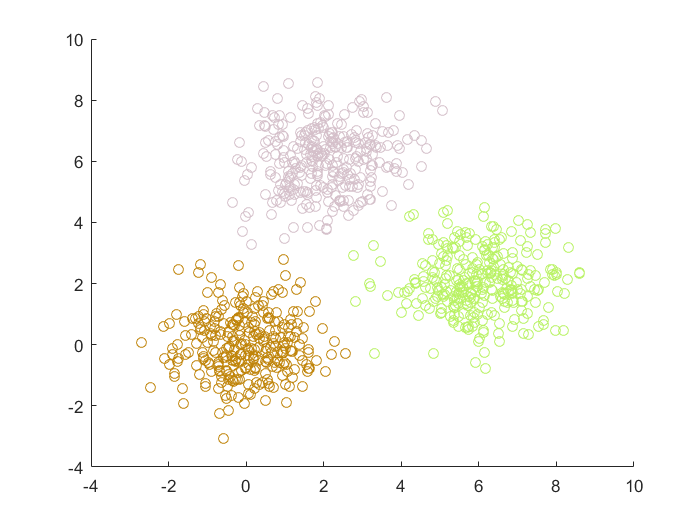
性能比较

优点：
- 对噪声数据不敏感
- 不依赖初始数据点的选择
- 可以完成任意形状的聚类

缺点：

算法复杂，分类速度较慢
需要在测试前确定密度阈值
对于高维数据，距离的度量并不是很好
不适合数据集密度差异较大或整体密度基本相同的情况