无监督学习
现实生活中常常会缺乏足够的先验知识,因此难以人工标注类别或进行人工类别标注的成本太高。很自然地,我们希望计算机能代我们完成这些工作,或至少提供一些帮助。根据类别未知(没有被标记)的训练样本解决模式识别中的各种问题,称之为无监督学习。
算法分类
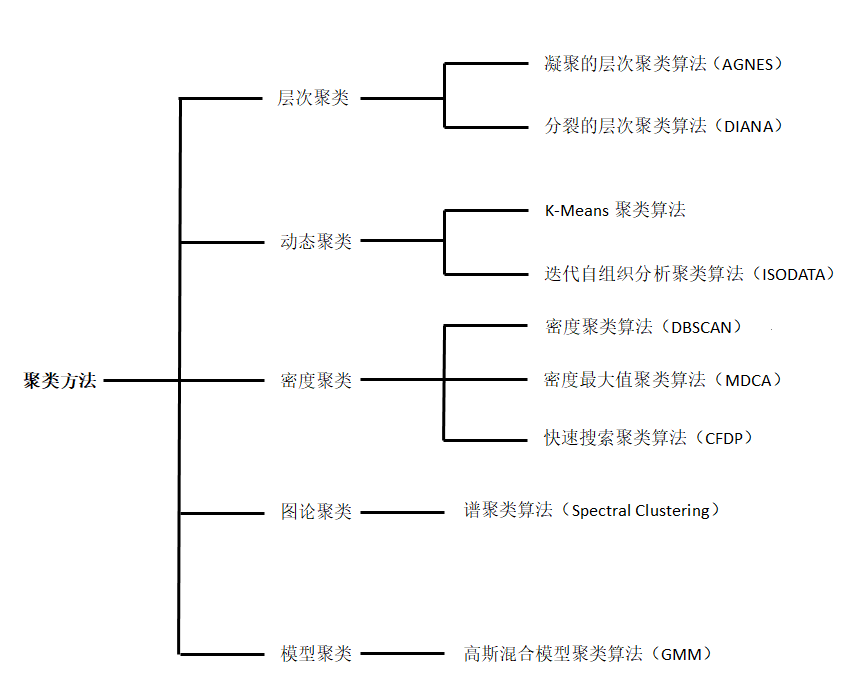
性能比较
所用数据集可以查看相关文档,数据集(Data Set)
凝聚的层次聚类(AGNES)
- 优点:
- 对噪声数据不敏感
- 算法简单,容易理解
- 不依赖初始值的选择
- 对于类别较多的训练集分类较快
- 缺点:
- 合并操作不能撤销
- 需要在测试前知道类别的个数
- 对于类别较少的训练集分类较慢
- 只适合分布呈凸型或者球形的数据集
- 对于高维数据,距离的度量并不是很好
分裂的层次聚类(DIANA)
- 优点:
- 算法简单,容易理解
- 不依赖初始值的选择
- 对于类别较少的训练集分类较快
- 缺点:
- 对噪声数据敏感
- 分裂操作不能撤销
- 需要在测试前知道类别的个数
- 对于类别较多的训练集分类较慢
- 只适合分布呈凸型或者球形的数据集
- 对于高维数据,距离的度量并不是很好
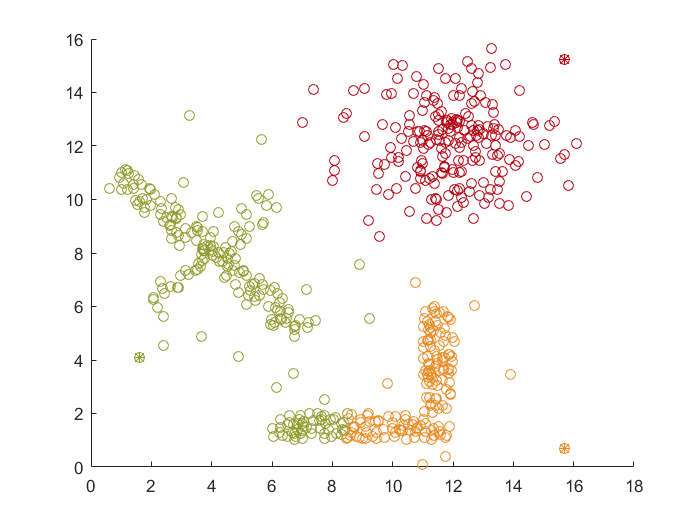
K均值聚类(K-MEANS)
- 优点:
- 算法简单,容易理解
- 大数据集时,对噪声数据不敏感
- 缺点:
- 对初始中心点敏感
- 需要在测试前知道类别的个数
- 只适合分布呈凸型或者球形的数据集
- 对于高维数据,距离的度量并不是很好
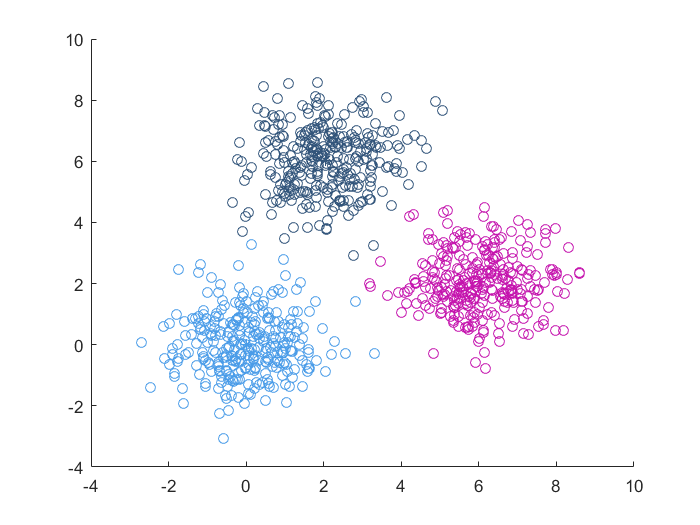
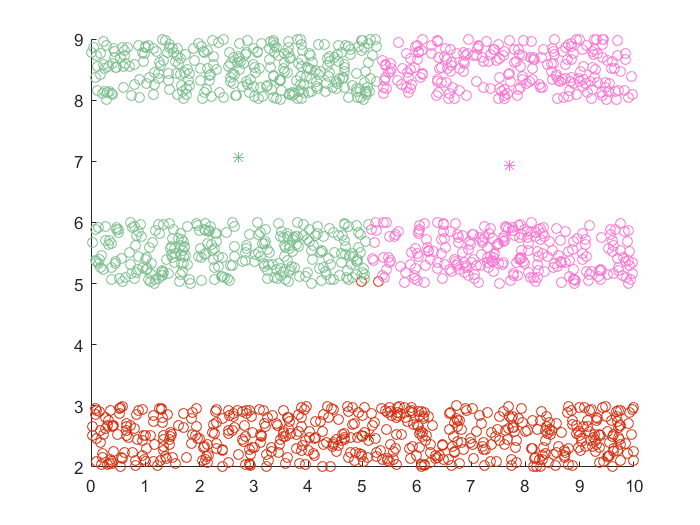
迭代自组织分析聚类(ISODATA)
- 优点:
- 大数据集时,对噪声数据不敏感
- 可以动态调整类别个数和类别中心
- 在先验知识不足的情况下有较好的分类能力
- 缺点:
- 对初始中心点敏感
- 算法复杂,分类速度较慢
- 只适合分布呈凸型或者球形的数据集
- 对于高维数据,距离的度量并不是很好
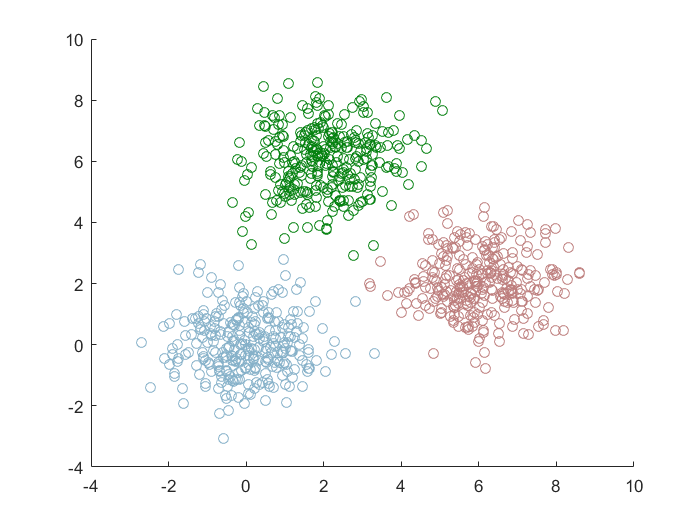
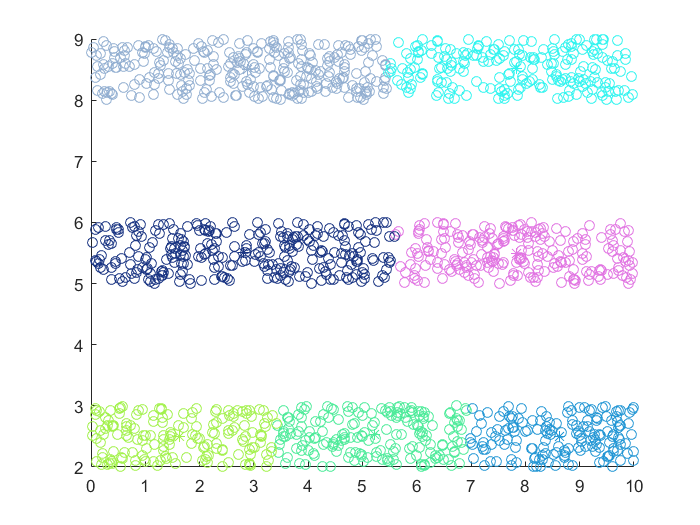
密度聚类(DBSCAN)
- 优点:
- 算法简单,容易理解
- 不依赖初始数据点的选择
- 可以完成任意形状的聚类
- 缺点:
- 对噪声数据敏感
- 需要在测试前确定eps和minPts
- 不适合数据集中密度差异较大的情况
- 对于高维数据,距离的度量并不是很好
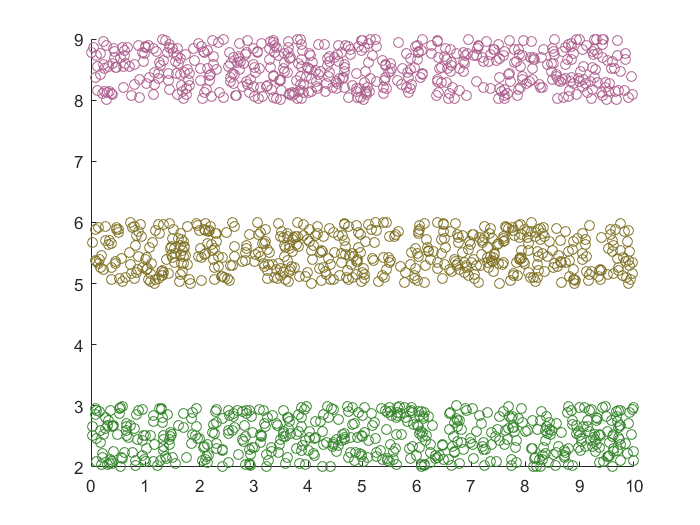
密度最大值聚类(MDCA)
- 优点:
- 对噪声数据不敏感
- 不依赖初始数据点的选择
- 可以完成任意形状的聚类
- 缺点:
- 算法复杂,分类速度较慢
- 需要在测试前确定密度阈值
- 对于高维数据,距离的度量并不是很好
- 不适合数据集密度差异较大或整体密度基本相同的情况
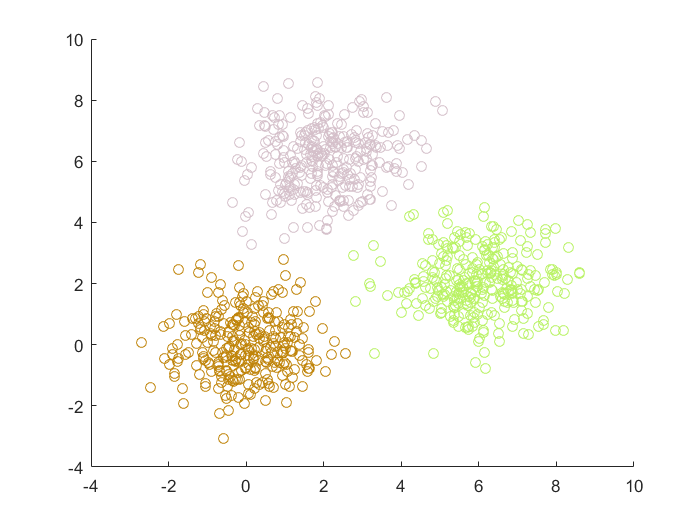
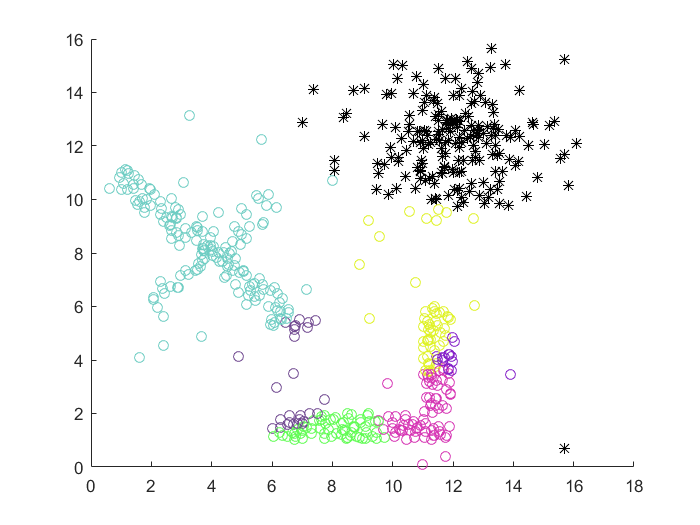
快速搜索聚类(CFDP)
- 优点:
- 对噪声数据不敏感
- 不依赖初始数据点的选择
- 可以完成任意形状的聚类
- 缺点:
- 离群点的确定非常复杂
- 算法复杂,分类速度较慢
- 对于高维数据,距离的度量并不是很好
- 不适合数据集整体密度基本相同的情况
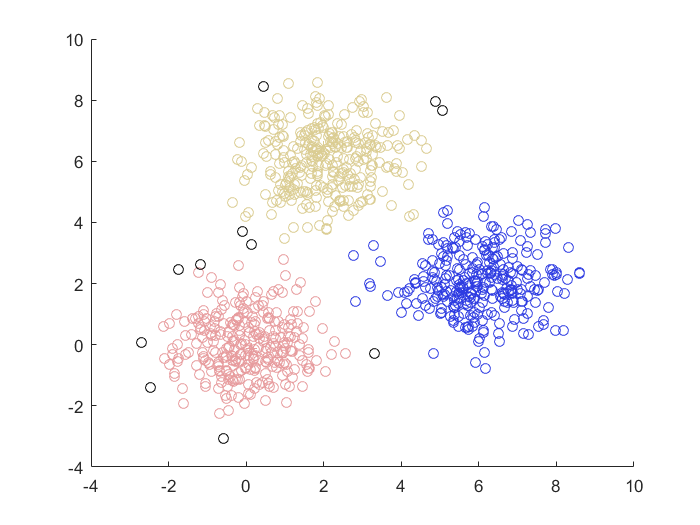
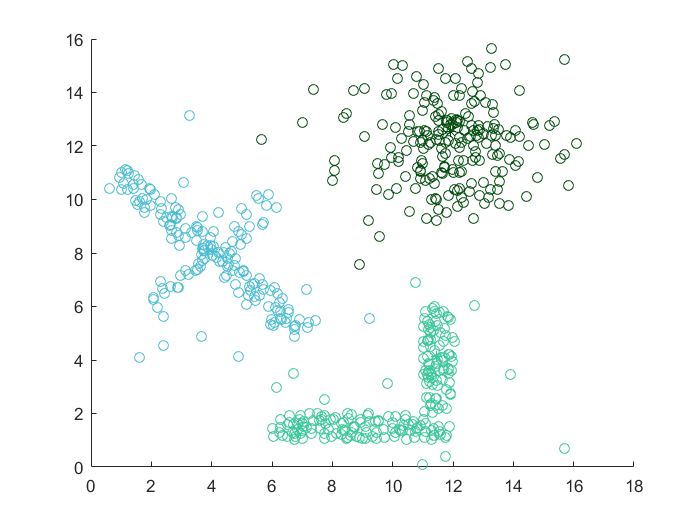
谱聚类(Spectral Clustering)
- 优点:
- 不依赖初始数据点的选择
- 使用了降维技术,适合于高维数据的聚类
- 建立在谱图理论,能在大部分形状聚类,收敛于全局最优解
- 缺点:
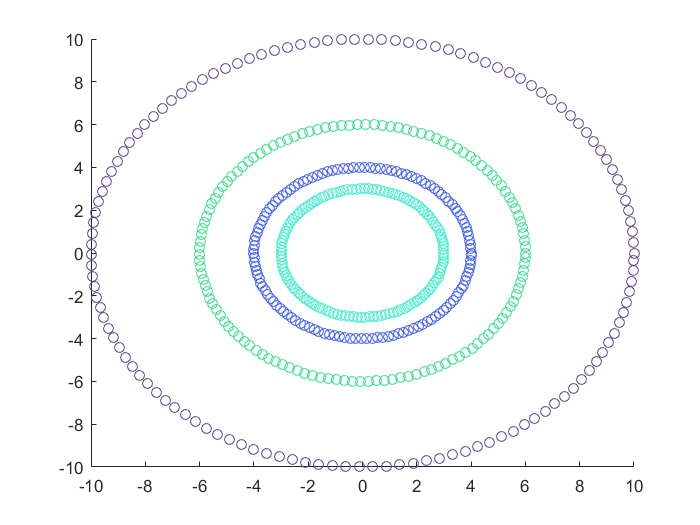
- 难以对圆形数据聚类
- 对噪声数据非常敏感
- 需要在测试前知道类别的个数
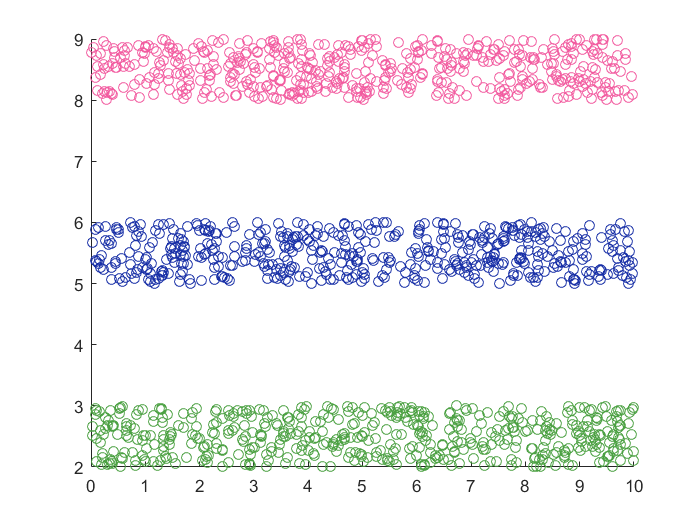
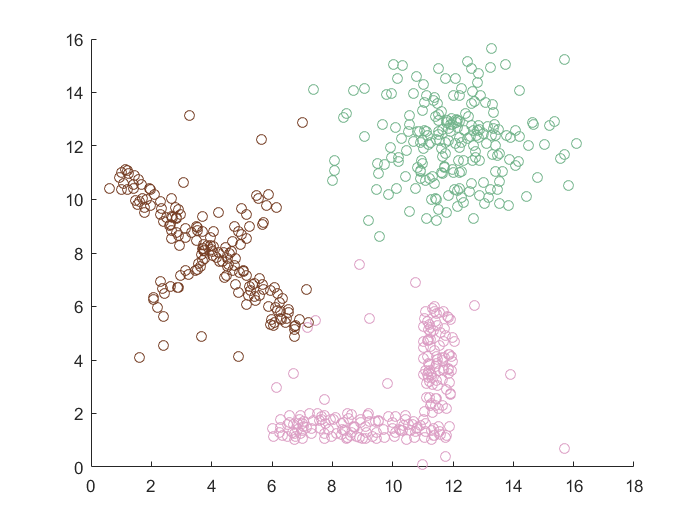
高斯混合模型聚类(GMM)
- 优点:
- 可以完成大部分形状的聚类
- 大数据集时,对噪声数据不敏感
- 对于距离或密度聚类,更适合高维特征
- 缺点:
- 计算复杂,速度较慢
- 难以对圆形数据聚类
- 需要在测试前知道类别的个数
- 初始化参数会对聚类结果产生影响
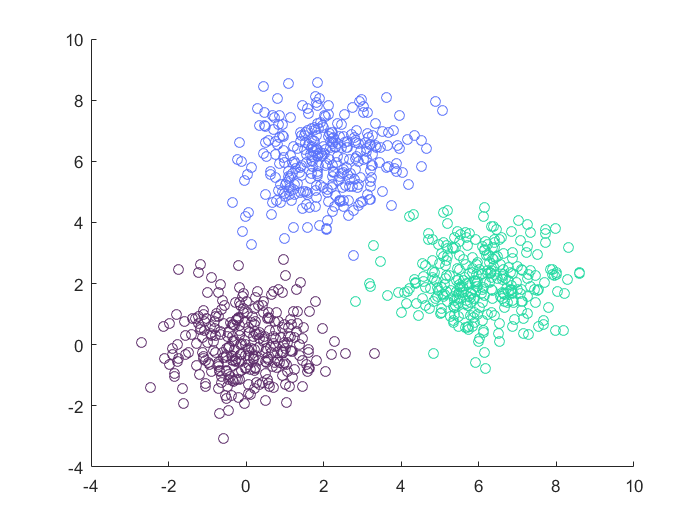
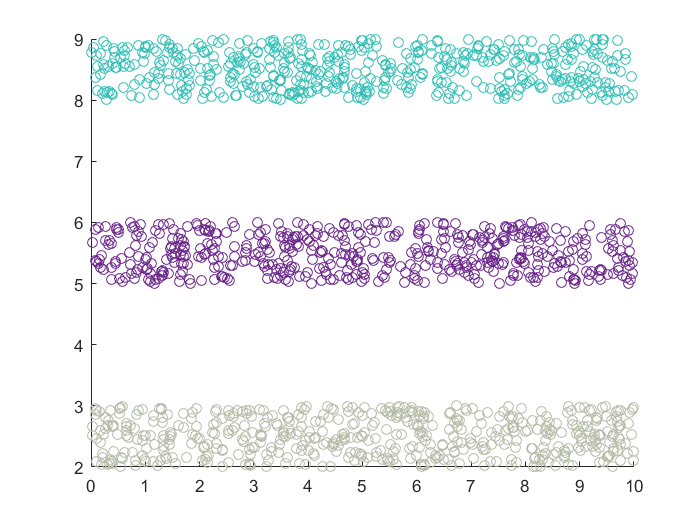
特点小结
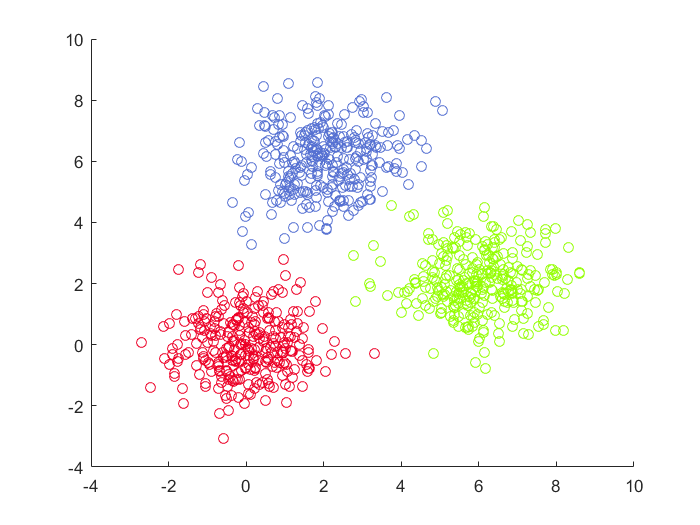
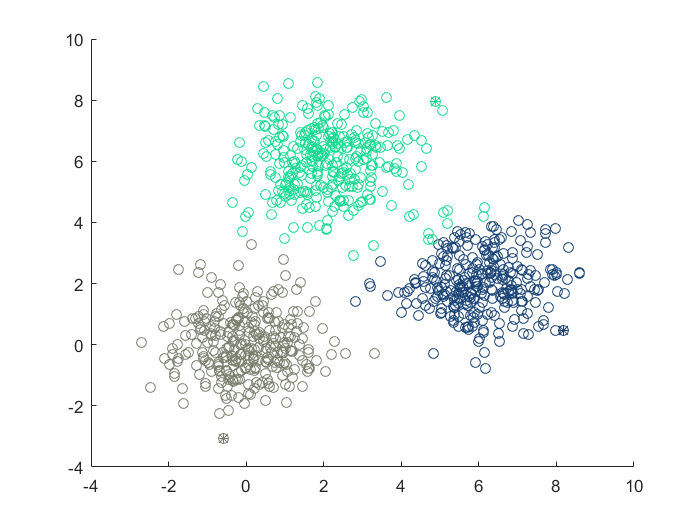
- 凸型或者球形分布的数据集,绝大部分算法都是可以适用的
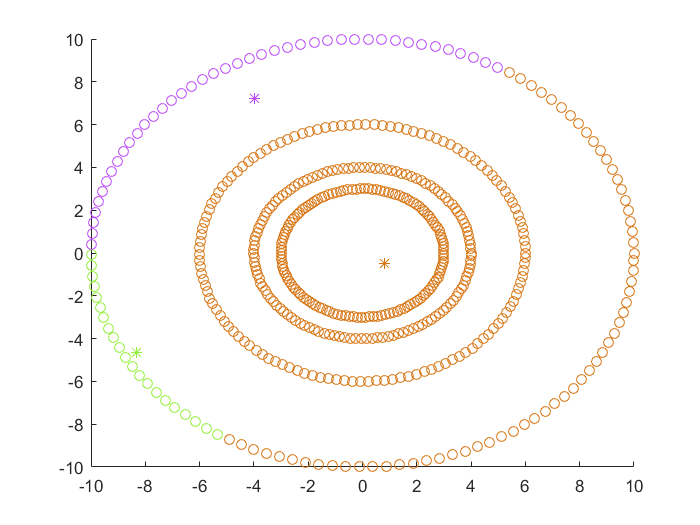
- 圆形分布的数据集,DBSCAN算法最为合适
- 线型分布的数据集,DBSCAN,Spectral Clustering,GMM都可以使用
- 高维特征最好使用Spectral Clustering或者GMM算法
- 密度算法大多适用于各类的密度峰值相差不大的情况
- 实际中可以通过已知的某些先验知识尝试去选择合适的算法